Il differenziale per l'autoveicolo - approfondimenti
- Autore discussione AVC-Staff
- Data d'inizio
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
al massimo, la ruota in aderenza trasferirà una coppia pari a
DELTA C = C2 – C1 = [(1 - β) / (1+β)] C
DELTA C = C2 – C1 = [(1 - β) / (1+β)] C
vediamo se avete capito
prendete questo disegno
eliminate la parte relativa al ripartitore di coppia (linea verde)
aggiungete, invece, la linea che dovrebbe tradurre la relazione che intercorre tra le coppie ai planetari di un differenziale a basso rendimento interno.
prendete questo disegno
eliminate la parte relativa al ripartitore di coppia (linea verde)
aggiungete, invece, la linea che dovrebbe tradurre la relazione che intercorre tra le coppie ai planetari di un differenziale a basso rendimento interno.
Allegati
:nono)bigno72":3nvy4ew3 ha detto:Dovrebbe essere parallela alla retta rossa, scostata di BETA; ma sugli assi non dovrei piu' avere DX e SX, bensi' LENTA e VELOCE.
Giusto?
:bonk)
Effettivamente se fosse scostata e parallela non incontrerebbe l'incrocio tra i due limiti di aderenza.
Riprovo: si incrocia nello stesso punto ma ha un "piede" sull'asse che rappresenta la ruota lenta. Piede non e' il termine corretto, lo so... .il piede rappresenterebbe lo scostamento della retta parallela.... (almeno in elettronica)
Meglio se provo a disegnarla
Riprovo: si incrocia nello stesso punto ma ha un "piede" sull'asse che rappresenta la ruota lenta. Piede non e' il termine corretto, lo so... .il piede rappresenterebbe lo scostamento della retta parallela.... (almeno in elettronica)
Meglio se provo a disegnarla
Allegati
Aggiungo 2 righe:
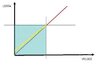
quando le due ruote non slittano la coppia e' ripartita equamente.
Quando una ruota inizia a slittare, il limite di coppia applicabile all'altra ruota scende, ma meno di quanto non scenda sulla ruota che sta slittando.
Quando una ruota e' sul ghiaccio (punto 0 sulle ascisse) , all'altra arriva ancora una certa coppia (il punto di partenza della retta gialla sulle ordinate)
quando le due ruote non slittano la coppia e' ripartita equamente.
Quando una ruota inizia a slittare, il limite di coppia applicabile all'altra ruota scende, ma meno di quanto non scenda sulla ruota che sta slittando.
Quando una ruota e' sul ghiaccio (punto 0 sulle ascisse) , all'altra arriva ancora una certa coppia (il punto di partenza della retta gialla sulle ordinate)
bigno72":2vvmu8qq ha detto:Effettivamente se fosse scostata e parallela non incontrerebbe l'incrocio tra i due limiti di aderenza.
Riprovo: si incrocia nello stesso punto ma ha un "piede" sull'asse che rappresenta la ruota lenta. Piede non e' il termine corretto, lo so... .il piede rappresenterebbe lo scostamento della retta parallela.... (almeno in elettronica)
Meglio se provo a disegnarla
:bonk) :bonk) :bonk) :bonk) :bonk) :bonk) :bonk) :bonk) :bonk) :bonk) :bonk)
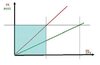
In condizioni di marcia rettilinea, allora, se non voglio trascurare il rendimento interno del differenziale, la ripartizione delle coppie motrici (dellA coppiA motricE su ciascuno dei due semiassi) rimane, in parte indeterminata. Queste coppie, infatti, possono variare tra i limiti estremi
[1/(1+β)] C e [β/(1+β)] C
su questo disegno il coefficiente angolare è il rapporto tra C(lenta) e C(veloce), quindi il rapporto tra le due grandezze può variare tra β e 1/β.
se β=1 siamo nel caso del diff "ideale" e della ripartizione perfetta 1/2 e 1/2 della coppia motrice (linea rossa centrale)

thranduil":2smaaw7n ha detto:In condizioni di marcia rettilinea, allora, se non voglio trascurare il rendimento interno del differenziale, la ripartizione delle coppie motrici (dellA coppiA motricE su ciascuno dei due semiassi) rimane, in parte indeterminata. Queste coppie, infatti, possono variare tra i limiti estremi
[1/(1+β)] C e [β/(1+β)] C
su questo disegno il coefficiente angolare è il rapporto tra C(lenta) e C(veloce), quindi il rapporto tra le due grandezze può variare tra β e 1/β.
se β=1 siamo nel caso del diff "ideale" e della ripartizione perfetta 1/2 e 1/2 della coppia motrice (linea rossa centrale)

ohhhhh :spin)
:spin) :spin) :spin)
sapevo che qualcuno mi avrebbe dato delle soddisfazioni!!
ebbbbravo!
infatti, basta prendere le formule di C1 (della ruota 1) e di C2 (della ruota 2) in funzione di C e risolverle in funzione una dell'altra....
diventa, per esempio,
C1 = (1/ β) C2 se la velocità angolare della ruota 2 è > di quella della ruota 1.
quindi, se ho aderenza 0 su una delle due ruote (es. ghiaccio), anche con un differenziale a basso rendimento interno mi sarà impossibile partire!!!
se, invece, ho una -seppr minima aderenza- posso trasferire sulla ruota ad elevata aderenza "un po' più" di coppia rispetto al differenziale "ideale" aperto.
ci siamo?
avete capito?
p.s. rossomandello: mi hai un po' deluso... :nod)
bigno: vedi di fare una cura di troffie.... :lol:
Ho bisogno di un po' di tempo per digerire il grafico di Thranduil: non riesco proprio a "leggerlo".
Inoltre, devo anche capire come mai fossi convinto che avessimo detto che con una ruota sul ghiaccio l'altra ruota ricevesse DELTAC/2 coppia, o qualcosa del genere (magari e' stata una risposta errata di qualcuno non prontamente cazziata, boh)
Devo digerirla un po' tutta sta storia insomma...
Inoltre, devo anche capire come mai fossi convinto che avessimo detto che con una ruota sul ghiaccio l'altra ruota ricevesse DELTAC/2 coppia, o qualcosa del genere (magari e' stata una risposta errata di qualcuno non prontamente cazziata, boh)
Devo digerirla un po' tutta sta storia insomma...
bigno72":3ooktwkm ha detto:Ho bisogno di un po' di tempo per digerire il grafico di Thranduil: non riesco proprio a "leggerlo".
Inoltre, devo anche capire come mai fossi convinto che avessimo detto che con una ruota sul ghiaccio l'altra ruota ricevesse DELTAC/2 coppia, o qualcosa del genere (magari e' stata una risposta errata di qualcuno non prontamente cazziata, boh)
Devo digerirla un po' tutta sta storia insomma...
perchè hai frainteso quello che ho scritto qui.
invece, il grafico di thranduil conferma chiaramente tutto quello scritto qui
alfistavero":3ooktwkm ha detto:ATTENTI BENE!
HO SCRITTO "SLITTA SUL GHIACCIO" PER FARVI CAPIRE che esiste una differenza di velocità tra i 2 planetari (quindi, tra i due semiassi).
correttezza (tecnica, e non teNNica) mi imporrebbe di scrivere semplicemnete "ruota più lenta" e "ruota più veloce" (dove la relazione tra lenta e veloce è data dalla solita formula di Willis).
anche perchè, come vedremo adesso, nel caso di differenziali NON "aperti" (e ideali, cioè con rendimento = 1), la coppia tra le due ruote (sia in curva, sia sul ghiaccio) NON si ripartice equamente (C/2 su entrambi i semiassi).
quindi, adesso per distinguere tra i due semiassi, dirò "semiasse più lento" e "semiasse più veloce".
alfistavero":34qegah3 ha detto:allora, non c'è nessuno?
a nessuno interessa più?
Io sono ancora interessato.
fin qui è chiaro?
è chiaro che in un differenziale "libero" -in curva- le coppie sono uguali (C/2 su ogni ruota) e che in un differenziale a basso rendimento interno, invece, le coppie sono differenti (maggiore sulla ruota interna, più lenta; e minore sulla ruota esterna, più veloce)?
è chiaro che in un differenziale "libero" -in curva- le coppie sono uguali (C/2 su ogni ruota) e che in un differenziale a basso rendimento interno, invece, le coppie sono differenti (maggiore sulla ruota interna, più lenta; e minore sulla ruota esterna, più veloce)?
alfistavero":2eq2mljx ha detto:fin qui è chiaro?
è chiaro che in un differenziale "libero" -in curva- le coppie sono uguali (C/2 su ogni ruota) e che in un differenziale a basso rendimento interno, invece, le coppie sono differenti (maggiore sulla ruota interna, più lenta; e minore sulla ruota esterna, più veloce)?
Sì.
alfistavero":25alv0w9 ha detto:p.s. rossomandello: mi hai un po' deluso... :nod)
Problema è che di solito non mangio trofie al pesto ma orecchiette... saranno quelle? :asd)
Scherzi a parte, ora mi torna, ma mi ero incartato a pensare a quel DELTA C/2 aggiunto e sottratto...
In ogni caso: quando un allievo dice una minchiata, la colpa è SEMPRE.....
.....dell'allievo che ha detto la minchiata! :fluffle)
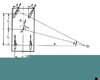
allora, guardate questa figura.
mettete la trazione dove volete (anteriore o posteriore, NON importa).
scegliete l'asse motore e applicate ad oggni ruota motrice la forza equivalente che traduce l'effetto della coppia motrice (ossia, tirate una freccia che parta dal centro ruota e sia parallela all'asse ruota: una freccia per ogni ruota), quindi pari a F = C / R dove R è il raggio della ruota...
la freccia più lunga andrà, naturalmente, sulla ruota che dà la coppia maggiore.....
...e domani ci divertiamo
mettete la trazione dove volete (anteriore o posteriore, NON importa).
scegliete l'asse motore e applicate ad oggni ruota motrice la forza equivalente che traduce l'effetto della coppia motrice (ossia, tirate una freccia che parta dal centro ruota e sia parallela all'asse ruota: una freccia per ogni ruota), quindi pari a F = C / R dove R è il raggio della ruota...
la freccia più lunga andrà, naturalmente, sulla ruota che dà la coppia maggiore.....
...e domani ci divertiamo