ok
grazie per le attestazioni di stima
tirèmm innanzi...
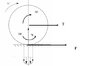
Prendiamo la nostra ruota. Abbiamo visto il punto C, centro di istantanea rotazione della ruota. Bene: C è anche il punto di contatto tra la ruota e la strada. Guardate la figura qui sotto.
Guardate il caso ideale (a).
Nel punto di contatto tra la ruota e la strada viene applicata la forza N che è la reazione vincolare della strada alla forza NORMALE (cioè perpendicolare) applicata alla ruota. Nel nostro caso, visto che siamo in piano, questa forza normale altro non è se non la forza peso della ruota (il carico applicato alla ruota). Questa forza peso altro non sarà se non il peso della ruota + la parte del peso dell’auto che compete alla ruota. Se ho solo la ruota e basta, sarà solo il peso della ruota.
Bene: nel caso ideale, il contatto tra ruota e strada è puntiforme (il punto C).
Peccato, però, che nella REALTA’ le cose vadano diversamente
In realtà, infatti, si tiene conto della deformabilità della ruota (cioè cerchio+pneumatico) e si ammette che il contatto del pneumatico con la strada non avvenga solo in un punto (il punto C), ma su una superficie limitata chiamata “orma di contatto” (o “superficie di contatto”). Questa superficie ha una sua propria grandezza, definita come “area dell’orma di contatto” (o “area della superficie di contatto”; o anche “area dell’impronta”).
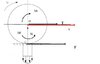
A questo punto, ci aggiungiamo anche che il pneumatico NON è perfettamente elastico: quando io deformo il pneumatico per farlo rotolare, gli do una certa energia che, dopo la deformazione, quando il pneumatico tende a riprendere la propria forma, non viene interamente restituita. Parte di questa energia, viene persa a causa delle dissipazioni (delle perdite) all’interno del materiale. Queste perdite sono dovute all’ISTERESI del materiale con cui sono fatti i pneumatici. Di conseguenza, si è visto sperimentalmente che per rotolare il pneumatico richiede di spendere una certa energia. Questo equivale ad una distribuzione delle pressioni la cui risultante è leggermente spostata in avanti nel senso del moto: guardate il disegno del caso reale (b) e confrontatelo con il caso ideale (a).
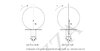
Come vedete, la forza N, che rappresenta la reazione vincolare della forza normale al terreno (nonché la risultante della distribuzione delle pressioni) è spostata in avanti rispetto al centro di istantanea rotazione. E guardate anche la distribuzione delle pressioni: nel caso ideale, tale distribuzione è simmetrica; nel caso reale, è asimmetrica con il picco verso l’avanti.
Questo rappresenta la spiegazione tecnica dell’isteresi del pneumatico. In pratica, anche senza applicare forze resistenti, la ruota, per rotolare, dissipa energia!!!
Naturalmente, l’energia persa è funzione della deformazione del pneumatico; quindi, delle caratteristiche costruttive del pneumatico stesso (tipo di materiale, tipo di pneumatico cioè se radiale o a tele incrociate; dimensioni del pneumatico, larghezza del battistrada, etc) e di caratteristiche esterne (pressione di gonfiaggio, carico verticale sul pneumatico, etc). Per esempio, i pneumatici “verdi” sono pneumatici realizzati con materiali “a bassa isteresi”, che si deformano poco; ma, per questo, “tengono” anche meno…
Charamente, tanto maggiore sarà l’isteresi del pneumatico, tanto maggiore sarà l’energia persa per il rotolamento, tanto maggiore l’energia necessaria per far rotolare il pneumatico…ciò equivale a “spostare” sempre più in avanti il punto di applicazione della forza N…
La coppia resistente (il momento resistente), rispetto al centro di rotazione O, sarà il prodotto della forza N moltiplicata per il braccio (la distanza del punto di applicazione di N) dal punto di contatto C: nel disegno, Mf = N u
Leggete, rileggete e mettetevelo bene in testa…
Poi andiamo avanti