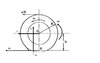
allora, andiamo avanti e definiamo il raggio sotto carico e vediamo dove va a finire il centro di rotazione della ruota vera....
guardate la figura che allego qui sotto: guardatela bene e comprendetela bene
Consideriamo una ruota di raggio R in rotolamento puro, cioè senza che su di essa agisca alcuna coppia motrice o frenante. Il centro della ruota si muove a velocità V e la ruota rotola con velocità angolare ω.
Il raggio di rotolamento è definito come il rapporto tra V e ω. Ossia, Ro = V/ ω.
Per farla breve, e semplice, si può dimostrare che Ro è compreso tra un valore minimo ed uno massimo. Il valore massimo è il valore del raggio della ruota scarica (cioè R); quello minimo, è l’altezza del centro della ruota sul suolo h (che prende il nome di raggio sotto carico).
Insomma, se scrivo quello che ho detto in termini matematici, avrò che h<Ro<R.
Quello che m’interessa che comprendiate è che la velocità periferica di ogni punto del battistrada VARIA CICLICAMENTE. Cioè, un qualunque punto del battistrada, se non è a contatto col suolo, dapprima, avrà all’inizio una velocità periferica pari a ωR. Quando però arriva a contatto col suolo, la sua velocità (periferica) rallenta e, partendo da ωR si avvicina sempre più a ωh.
Questo significa che in questa prima fase, cioè dalla condizione indeformata fino ad A, il punto del battistrada STRISCIA e rallenta. Quando arriva in A, però, la velocità non diventa ωh, ma rimane sempre superiore: cioè. Anche in A continua a strisciare (di poco, ma striscia).
Da A in poi, invece, il punto riaccelera per raggiungere nuovamente la velocità ωR della ruota indeformata. Cioè, dopo aver lasciato l’orma di contatto assume nuovamente la sua lunghezza iniziale e ritorna la valore iniziale ωR.
Se guardate il grafico che c’è allegato nel disegno, vedete come varia la velocità del singolo punto del battistrada con il rotolamento….
Questo significa che, nel primo tratto (cioè nella fase in cui rallenta passando da ωR per portarsi verso ωh in A) il battistrada si comprime, STRISCIA e rallenta; nel secondo tratto (cioè nella fase in cui riaccelera passando da A per portarsi verso la zona indeformata), il battistrada si estende, STRISCIA e riaccelera. Ma sempre striscia….
Il punto A, quindi, NON è il centro di istantanea rotazione (quello che prima abbiamo chiamato C) della ruota. Il nostro centro di istantanea rotazione, infatti, NON è più sul piano stradale, ma SOTTO il piano della strada!!!! Il mio C sta sotto A!!! e tanto più la mia pancia è pronunciata, tanto più in basso andrà C, tanto maggiore sarà lo strisciamento del battistrada in A….
Prima considerazione. Questo è il motivo per cui i pneumatici si consumano: perché strisciano sull’asfalto. Anche se decideste di non fare più curve per il resto dei vostri giorni di guida, consumereste le gomme ugualmente. Ora, è chiaro che il valore di h (cioè del raggio sotto carico) dipende da un sacco di fattori, alcuni dipendenti dal pneumatico (come la struttura della carcassa, dallo stato di usura del pneus stesso, etc); altri dipendenti dalle condizioni di impiego (pressione di gonfiaggio, carico, velocità, etc). per esempio, i pneumatici radiali hanno valori di h minori rispetto ai pneus a tele incociate a pari raggio indeformato R (può sembrare strano, ma è proprio così e dipende dal fatto che il radiale ha una maggiore flessibilità radiale; però hanno valori di Ro meno lontani dal valore di R, cioè il raggio di rotolamento è più prossimo al valore del raggio indeformato).
Però deve essere ben chiaro che, anche se gonfiate tantissimo le gomme, anche se riducete il carico sul pneumatico, comunque, avrete un valore di h inferiore rispetto al valore del raggio di rotolamento e al raggio R indeformato. Cioè, una deformazione ce l’avrete sempre.
Poi, è chiaro che se aumentate il carico o riducete la pressione di gonfiaggio avrete una diminuzione di h e del raggio di rotolamento, mentre vi capiterà il contrario se gonfiate tanto o riducete il carico…questo lo capite benissimo anche voi…
Seconda considerazione: la velocità angolare ω di una ruota dotata di pneumatico è SEMPRE MINORE di una ruota perfettamente rigida (per esempio, che so, di acciaio: un cerchione, tanto per fare un esempio che possiate capire tutti) con pari raggio sotto carico (cioè h, cioè altezza del centro ruota dal suolo)e pari velocità di traslazione (V).
Guardate di capirla bene, questa storia, perché sta alla base di tutto il resto: dalla motricità alla frenatura al funzionamento dell’ABS (lo vedremo!) alla resistenza la rotolamento….
Mi sa che per oggi è meglio mollarla qui, perché non avete idea di quanta carne al fuoco abbiamo messo!!
Domani ridiamo: tiriamo in ballo gli “sgommamenti”!!!
p.s. se avete dubbi, sparate senza problemi: al limite, vi do' dei ciaparàtt....:lol: :lol:
guardate la figura che allego qui sotto: guardatela bene e comprendetela bene
Consideriamo una ruota di raggio R in rotolamento puro, cioè senza che su di essa agisca alcuna coppia motrice o frenante. Il centro della ruota si muove a velocità V e la ruota rotola con velocità angolare ω.
Il raggio di rotolamento è definito come il rapporto tra V e ω. Ossia, Ro = V/ ω.
Per farla breve, e semplice, si può dimostrare che Ro è compreso tra un valore minimo ed uno massimo. Il valore massimo è il valore del raggio della ruota scarica (cioè R); quello minimo, è l’altezza del centro della ruota sul suolo h (che prende il nome di raggio sotto carico).
Insomma, se scrivo quello che ho detto in termini matematici, avrò che h<Ro<R.
Quello che m’interessa che comprendiate è che la velocità periferica di ogni punto del battistrada VARIA CICLICAMENTE. Cioè, un qualunque punto del battistrada, se non è a contatto col suolo, dapprima, avrà all’inizio una velocità periferica pari a ωR. Quando però arriva a contatto col suolo, la sua velocità (periferica) rallenta e, partendo da ωR si avvicina sempre più a ωh.
Questo significa che in questa prima fase, cioè dalla condizione indeformata fino ad A, il punto del battistrada STRISCIA e rallenta. Quando arriva in A, però, la velocità non diventa ωh, ma rimane sempre superiore: cioè. Anche in A continua a strisciare (di poco, ma striscia).
Da A in poi, invece, il punto riaccelera per raggiungere nuovamente la velocità ωR della ruota indeformata. Cioè, dopo aver lasciato l’orma di contatto assume nuovamente la sua lunghezza iniziale e ritorna la valore iniziale ωR.
Se guardate il grafico che c’è allegato nel disegno, vedete come varia la velocità del singolo punto del battistrada con il rotolamento….
Questo significa che, nel primo tratto (cioè nella fase in cui rallenta passando da ωR per portarsi verso ωh in A) il battistrada si comprime, STRISCIA e rallenta; nel secondo tratto (cioè nella fase in cui riaccelera passando da A per portarsi verso la zona indeformata), il battistrada si estende, STRISCIA e riaccelera. Ma sempre striscia….
Il punto A, quindi, NON è il centro di istantanea rotazione (quello che prima abbiamo chiamato C) della ruota. Il nostro centro di istantanea rotazione, infatti, NON è più sul piano stradale, ma SOTTO il piano della strada!!!! Il mio C sta sotto A!!! e tanto più la mia pancia è pronunciata, tanto più in basso andrà C, tanto maggiore sarà lo strisciamento del battistrada in A….
Prima considerazione. Questo è il motivo per cui i pneumatici si consumano: perché strisciano sull’asfalto. Anche se decideste di non fare più curve per il resto dei vostri giorni di guida, consumereste le gomme ugualmente. Ora, è chiaro che il valore di h (cioè del raggio sotto carico) dipende da un sacco di fattori, alcuni dipendenti dal pneumatico (come la struttura della carcassa, dallo stato di usura del pneus stesso, etc); altri dipendenti dalle condizioni di impiego (pressione di gonfiaggio, carico, velocità, etc). per esempio, i pneumatici radiali hanno valori di h minori rispetto ai pneus a tele incociate a pari raggio indeformato R (può sembrare strano, ma è proprio così e dipende dal fatto che il radiale ha una maggiore flessibilità radiale; però hanno valori di Ro meno lontani dal valore di R, cioè il raggio di rotolamento è più prossimo al valore del raggio indeformato).
Però deve essere ben chiaro che, anche se gonfiate tantissimo le gomme, anche se riducete il carico sul pneumatico, comunque, avrete un valore di h inferiore rispetto al valore del raggio di rotolamento e al raggio R indeformato. Cioè, una deformazione ce l’avrete sempre.
Poi, è chiaro che se aumentate il carico o riducete la pressione di gonfiaggio avrete una diminuzione di h e del raggio di rotolamento, mentre vi capiterà il contrario se gonfiate tanto o riducete il carico…questo lo capite benissimo anche voi…
Seconda considerazione: la velocità angolare ω di una ruota dotata di pneumatico è SEMPRE MINORE di una ruota perfettamente rigida (per esempio, che so, di acciaio: un cerchione, tanto per fare un esempio che possiate capire tutti) con pari raggio sotto carico (cioè h, cioè altezza del centro ruota dal suolo)e pari velocità di traslazione (V).
Guardate di capirla bene, questa storia, perché sta alla base di tutto il resto: dalla motricità alla frenatura al funzionamento dell’ABS (lo vedremo!) alla resistenza la rotolamento….
Mi sa che per oggi è meglio mollarla qui, perché non avete idea di quanta carne al fuoco abbiamo messo!!
Domani ridiamo: tiriamo in ballo gli “sgommamenti”!!!
p.s. se avete dubbi, sparate senza problemi: al limite, vi do' dei ciaparàtt....:lol: :lol: