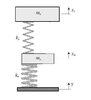
Ora,
Guardiamo l’equazione di moto del sistema molla-massa
x(t) = A cos (ωt + φ)
tralasciamo i valori A e φ, che sono cose che possiamo benissimo lasciare da parte per il momento.
Concentriamoci sulla frequenza propria. Cioè su ω
Questa vale, come detto SQR(k/m), ossia radice quadrata di k/m
k è la costante elastica della molla
m è la massa (della mia porzione di macchina)
ω è dunque la frequenza propria del sistema. E si misura in Hertz (Hz)
chiaro, a questo punto, che io possa determinare anche il periodo di oscillazione, ossia il tempo che intercorre tra due istanti uguali della mia oscillazione
il periodo è T = 2 / ω
ossia T = 2 * (PIgreco) / SQR(k/m)
cosa significa tutto ciò?
Significa questo:
la mia macchina, schematizzata come una massa m su molla k, se sottoposta ad un’azione perturbatrice (irregolarità del terreno), incomincerà ad oscillare. Oscillerà con una certa frequenza, che dipende dalla massa della macchina e dalla rigidezza della molla.
L’accelerazione che subirà la mia massa, cioè la mia scocca (o la parte di scocca di massa m con cui ho schematizzato la macchina) dipenderà dalla frequenza dell’eccitazione dovuta alla strada. Ossia, se la mia strada ha una certa ondulazione e io la percorro avanti e indietro a velocità crescenti, la mia scocca (la massa m) comincierà ad oscillare sempre più. Data la strada e la sua ondulazione, posso modificare la frequenza con cui “eccito” la scocca semplicemente percorrendo la strada a velocità differenti. Provate a pensarci. Supponiamo che comincio a bassissima velocità. La mia scocca comincia ad oscillare piano. Poi aumento un po’ la velocità; e la scocca oscilla sempre un po’ di più. La mia scocca sarà sottoposta ad accelerazioni sempre maggiori perché la mia eccitante (la strada ondulata) “eccita”, appunto, sempre più la scocca.
Ad un certo punto, arriverò a percorrere la strada ondulata ad una velocità tale che la frequenza delle mie oscillazioni eccitanti coincidono con la frequenza propria della mia macchina ω = SQR(k/m). In questo caso, l’accelerazione della scocca (cioè della mia massa m) diventerà elevatissima: questo significa che la strada, percorsa a quella determinata velocità, ha eccitato la frequenza propria della mia macchina. Cioè l’eccitante (la strada) ha frequenza pari alla frequenza propria del mio sistema (sistema molla-massa).
Chiaramente, se a quella velocità avessi una macchina diversa (cioè con m diversa) o mettessi una molla diversa (ossia con un diverso k), la mia frequenza propria sarebbe differente (maggiore o minore di prima) e quindi manderei “in risonanza” la macchina ad una velocità differente (maggiore o minore) su quella determinata strada. Precisamente, se aumento la rigidezza k della molla, la mia frequenza aumenterà (k è al numeratore); se aumento m, la mia frequenza diminuirà (m è al denominatore). Se diminuisco l’una o l’altra, succederà il contrario. se modifico l’una E l’altra, dipende dall’entità delle due modifiche.
Questo è quello che succede se viaggio con una macchina dotata solamente di molle (senza ammortizzatori). In pratica, la mia scocca continuerà ad oscillare e, facilmente, mi troverò in condizioni di “risonanza”. E guardate che è abbastanza facile trovarsi in quelle condizioni, perché la frequenza propria della cassa, della scocca, è piuttosto bassa, nell’ordine dell’1,5 Hz. Avete capito bene: 1,5 Hz. Uè, se proprio vogliamo esagerare e comprendere tutti i tipi di scocca, diciamo che la frequenza propria di una scocca varia tra 1 e 2 Hz (proprio a voler stare larghi). Le frequenza maggiori sono proprie delle vetture con scocca più rigida.
E se mi trovo in condizioni di risonanza, significa che “spicco il volo” con la scocca. Ossia, la mia scocca (e tutto quello che c’è dentro) subirà delle accelerazioni molto molto elevate.
Per farvi capire meglio il problema, allego questo grafico.
Sull’asse delle ascisse c’è la frequenza delle mie forze perturbatrici (eccitanti). Perché comprendiate meglio, fate finta che su quell’asse ci sia la velocità con cui percorrete la strada ondulata (sempre quella). Sull’asse delle ordinate viene riportata l’accelerazione (quindi la forza, se la moltiplico per la massa m) che la massa m (cioè la scocca) subisce.
Vedete che, in corrispondenza della frequenza di risonanza del mio sistema molla-massa le accelerazioni hanno un picco? Bene: questo significa che in quel caso, sto eccitando la mia massa m (sospesa dalla molla k) con una frequenza che coincide con la “frequenza propria” del mio sistema molla-massa. Sono, cioè, in condizioni di “risonanza”. Quel valore, dove c’è la freccia è un valore che sta nell’intorno di 1,5 Hz. E questo, mi può benissimo capitare su una strada qualunque: basta che affronti le sconnessioni (le ondulazioni) della strada alla velocità “giusta”.
Fin qui, ci siamo?
Guardiamo l’equazione di moto del sistema molla-massa
x(t) = A cos (ωt + φ)
tralasciamo i valori A e φ, che sono cose che possiamo benissimo lasciare da parte per il momento.
Concentriamoci sulla frequenza propria. Cioè su ω
Questa vale, come detto SQR(k/m), ossia radice quadrata di k/m
k è la costante elastica della molla
m è la massa (della mia porzione di macchina)
ω è dunque la frequenza propria del sistema. E si misura in Hertz (Hz)
chiaro, a questo punto, che io possa determinare anche il periodo di oscillazione, ossia il tempo che intercorre tra due istanti uguali della mia oscillazione
il periodo è T = 2 / ω
ossia T = 2 * (PIgreco) / SQR(k/m)
cosa significa tutto ciò?
Significa questo:
la mia macchina, schematizzata come una massa m su molla k, se sottoposta ad un’azione perturbatrice (irregolarità del terreno), incomincerà ad oscillare. Oscillerà con una certa frequenza, che dipende dalla massa della macchina e dalla rigidezza della molla.
L’accelerazione che subirà la mia massa, cioè la mia scocca (o la parte di scocca di massa m con cui ho schematizzato la macchina) dipenderà dalla frequenza dell’eccitazione dovuta alla strada. Ossia, se la mia strada ha una certa ondulazione e io la percorro avanti e indietro a velocità crescenti, la mia scocca (la massa m) comincierà ad oscillare sempre più. Data la strada e la sua ondulazione, posso modificare la frequenza con cui “eccito” la scocca semplicemente percorrendo la strada a velocità differenti. Provate a pensarci. Supponiamo che comincio a bassissima velocità. La mia scocca comincia ad oscillare piano. Poi aumento un po’ la velocità; e la scocca oscilla sempre un po’ di più. La mia scocca sarà sottoposta ad accelerazioni sempre maggiori perché la mia eccitante (la strada ondulata) “eccita”, appunto, sempre più la scocca.
Ad un certo punto, arriverò a percorrere la strada ondulata ad una velocità tale che la frequenza delle mie oscillazioni eccitanti coincidono con la frequenza propria della mia macchina ω = SQR(k/m). In questo caso, l’accelerazione della scocca (cioè della mia massa m) diventerà elevatissima: questo significa che la strada, percorsa a quella determinata velocità, ha eccitato la frequenza propria della mia macchina. Cioè l’eccitante (la strada) ha frequenza pari alla frequenza propria del mio sistema (sistema molla-massa).
Chiaramente, se a quella velocità avessi una macchina diversa (cioè con m diversa) o mettessi una molla diversa (ossia con un diverso k), la mia frequenza propria sarebbe differente (maggiore o minore di prima) e quindi manderei “in risonanza” la macchina ad una velocità differente (maggiore o minore) su quella determinata strada. Precisamente, se aumento la rigidezza k della molla, la mia frequenza aumenterà (k è al numeratore); se aumento m, la mia frequenza diminuirà (m è al denominatore). Se diminuisco l’una o l’altra, succederà il contrario. se modifico l’una E l’altra, dipende dall’entità delle due modifiche.
Questo è quello che succede se viaggio con una macchina dotata solamente di molle (senza ammortizzatori). In pratica, la mia scocca continuerà ad oscillare e, facilmente, mi troverò in condizioni di “risonanza”. E guardate che è abbastanza facile trovarsi in quelle condizioni, perché la frequenza propria della cassa, della scocca, è piuttosto bassa, nell’ordine dell’1,5 Hz. Avete capito bene: 1,5 Hz. Uè, se proprio vogliamo esagerare e comprendere tutti i tipi di scocca, diciamo che la frequenza propria di una scocca varia tra 1 e 2 Hz (proprio a voler stare larghi). Le frequenza maggiori sono proprie delle vetture con scocca più rigida.
E se mi trovo in condizioni di risonanza, significa che “spicco il volo” con la scocca. Ossia, la mia scocca (e tutto quello che c’è dentro) subirà delle accelerazioni molto molto elevate.
Per farvi capire meglio il problema, allego questo grafico.
Sull’asse delle ascisse c’è la frequenza delle mie forze perturbatrici (eccitanti). Perché comprendiate meglio, fate finta che su quell’asse ci sia la velocità con cui percorrete la strada ondulata (sempre quella). Sull’asse delle ordinate viene riportata l’accelerazione (quindi la forza, se la moltiplico per la massa m) che la massa m (cioè la scocca) subisce.
Vedete che, in corrispondenza della frequenza di risonanza del mio sistema molla-massa le accelerazioni hanno un picco? Bene: questo significa che in quel caso, sto eccitando la mia massa m (sospesa dalla molla k) con una frequenza che coincide con la “frequenza propria” del mio sistema molla-massa. Sono, cioè, in condizioni di “risonanza”. Quel valore, dove c’è la freccia è un valore che sta nell’intorno di 1,5 Hz. E questo, mi può benissimo capitare su una strada qualunque: basta che affronti le sconnessioni (le ondulazioni) della strada alla velocità “giusta”.
Fin qui, ci siamo?