Bene
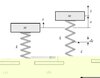
Se guardo la massa a destra, sempre nel mio disegno, vedo che questa è spostata di una certa quantità (x) rispetto alla posizione indeformata. Questo significa che la mia massa m si sta muovendo rispetto alla posizione di equilibrio (per esempio, perché ho preso una buca, o una sconnessione della strada). Quindi, significa anche che la mia molla, che in condizioni di equilibrio era compressa di una certa quantità per generare una forza che sostenesse il peso della massa m, sta generando una forza F proporzionale alla sua elongazione x. Cioè, F = k x
Adesso, se applico la legge di Newton che recita F = m a (tanto per essere precisi, va però detto che quando gli cadde in testa la mela perché dormiva sotto l’albero NON ha scritto la sua famosa legge nella forma F = m a , bensì nella forma F = dQ/dt, ossia derivata della quantità di moto rispetto al tempo. Ora, siccome la quantità di moto Q vale Q = m v, la formula di Newton diventa F = m (dv/dt) + v (dm/dt). Questa formuletta è quella usata dalla NASA per mettere in orbita lo Shuttle: basta tenere in considerazione che dm/dt è il flusso dei gas della combustione, che escono dagli ugelli a velocità v…bah, un giorno, magari, vedremo quali regolette, semplici semplici, stanno alla base della messa in orbita dei missili….torniamo a noi: noi supponiamo, con buona approssimazione, che la massa m non cambi, per cui il mio termine dm/dt è uguale a 0. quindi, rimane solo che F = m (dv/dt) cioè F = m a)
Detto tutto ciò, andiamo avanti
Avrò che F = m a dove
F = k x anzi a –k x perché la forza elastica si oppone al moto della massa m
mentre m a diventa m (dv/dt) = m (d2x/dt2) = m x” (con x” ho indicato la derivata seconda dello spostamento)
quindi
m x” – k x = 0
cioè x” – (k/m) x = 0
ora, se pongo ω2 = k/m
riscrivo il tutto come x” - ω2 x = 0
questa è la legge di moto che descrive, appunto, il movimento della mia massa m sostenuta dalla molla. Ma questa è anche un’equazione differenziale (a coeff. costanti) del second’ordine.
L’integrale (cioè la soluzione) di questa equazione è
x(t) = A cos (ωt + φ)
che è l’equazione di un moto armonico.
A e φ sono due coefficienti che dipendono dalle condizioni iniziali del sistema (es. da quando comincio a misurare, etc).
Quello che importa, invece, è il valore ω, che prende il nome di
frequenza propria del sistema
e vale, appunto, ω = sqrt (k/m) (ossia radice quadrata di k/m)
oggi, vediamo cosa vuol dire questo