La sospensione dell'autoveicolo - approfondimenti
- Autore discussione yugs
- Data d'inizio
lascia perdere: ora siamo ancora a livello di definizione di cosa è l'angolo di derivabigno72":1qnkemnw ha detto:
poi arriverà il momento in cui viene spiegato quando è diverso da zero e perchè
bigno72":2dlaq7h2 ha detto:
uuuuhhhhhhhh, che scassaminkia che sei...NO. e dovresti saperlo....e poi, cosa c'entra: ti ho appena spiegato che la deriva sarebbe l'angolo tra il vettore velocita' e l'asse del pneumatico. Mo' mi dici dove sarebbe diretto il vettore velocita' in caso di ruota in rotolamento puro come descritto giorni fa (e, quindi, quanto varrebbe l'angolo di deriva)?
comunque, mi sa che hai sbagliato a fare la domanda, intendendo se una ruota con camber (visto che se ne parlava prima) offre piu' o meno resistenza la rotolamento...risposta: SI
AVVISO AI NAVIGANTI ( ):
settimana prossima, da lunedi' a mercoledi' -sicuramente; e probabilmente pure giovedi'- per necessita' contingenti (sessioni di test congiunte con tecnici di altra societa'), il prosequio delle attivita' didattiche :lol: sara' rallentato (per non dire sospeso). si riprendera' in maniera intensa venerdi' (anche se non e' detto che risca a postare qualcosina)....
):settimana prossima, da lunedi' a mercoledi' -sicuramente; e probabilmente pure giovedi'- per necessita' contingenti (sessioni di test congiunte con tecnici di altra societa'), il prosequio delle attivita' didattiche :lol: sara' rallentato (per non dire sospeso). si riprendera' in maniera intensa venerdi' (anche se non e' detto che risca a postare qualcosina)....
andiamo avanti.
ho detto stamattina cosa sia l'angolo di deriva (angolo formato dal vettore velocita' con l'asse del pneumatico).
attenzione: l'angolo di deriva NON e' l'angolo di sterzo!!!!
NON CONFONDETELO CON L'ANGOLO DI STERZO!!!
l'angolo di sterzo e' l'angolo di cui le ruote sono ruotate a causa dell'azione imposta sul volante: io giro il volante di tot gradi e le ruote formano un angolo, rispetto all'asse della vettura, di un certo valore (poi vedremo che questo valore non e' uguale per la ruota dx e per quella sx).
si definisce un RAPPORTO DI STERZO -indicato in genere con la lettera greca tau (τ)- cosi' definito
τ = Av/Ar dove
Av e' l'angolo volante (cioe' di quanto giro il volante partendo dalla posizione 0 corrispondente alle ruote diritte)
Ar e' l'angolo di cui ruotano le ruote
tanto per intenderci, la 147 ha (aveva) un τ di 11 a fronte di una media del mercato di 17 (le migliori hanno/avevano 16)....tanto per dire, eh...
comunque, andiamo avanti:
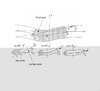
l-angolo di sterzo COMPRENDE l'angolo di deriva. guardate il disegno qui sotto e capirete: quello indicato con la lettera greca delta (δ) dorata e' l'anfgolo di sterzo; quello con αf (angolo di deriva forward, cioe' davanti) e' appunto l'angolo di deriva.
e qcon questo, buon week end, CIAPARA'TT!!!
ho detto stamattina cosa sia l'angolo di deriva (angolo formato dal vettore velocita' con l'asse del pneumatico).
attenzione: l'angolo di deriva NON e' l'angolo di sterzo!!!!
NON CONFONDETELO CON L'ANGOLO DI STERZO!!!
l'angolo di sterzo e' l'angolo di cui le ruote sono ruotate a causa dell'azione imposta sul volante: io giro il volante di tot gradi e le ruote formano un angolo, rispetto all'asse della vettura, di un certo valore (poi vedremo che questo valore non e' uguale per la ruota dx e per quella sx).
si definisce un RAPPORTO DI STERZO -indicato in genere con la lettera greca tau (τ)- cosi' definito
τ = Av/Ar dove
Av e' l'angolo volante (cioe' di quanto giro il volante partendo dalla posizione 0 corrispondente alle ruote diritte)
Ar e' l'angolo di cui ruotano le ruote
tanto per intenderci, la 147 ha (aveva) un τ di 11 a fronte di una media del mercato di 17 (le migliori hanno/avevano 16)....tanto per dire, eh...
comunque, andiamo avanti:
l-angolo di sterzo COMPRENDE l'angolo di deriva. guardate il disegno qui sotto e capirete: quello indicato con la lettera greca delta (δ) dorata e' l'anfgolo di sterzo; quello con αf (angolo di deriva forward, cioe' davanti) e' appunto l'angolo di deriva.
e qcon questo, buon week end, CIAPARA'TT!!!
Allegati
‘giorno
Fuoco o non fuoco, noi andiamo avanti (NOI TIREREMO DIRITTO....) anche se piano piano in modo che capiate bene questi argomenti.
Dopo aver chiarito bene cosa sia l’angolo di deriva del pneumatico, vediamo le forze scambiate tra pneus e strada in direzione trasversale.
Se il pneus si muove con un certo angolo di deriva, la forma della zona di contatto risulta notevolmente distorta.
Guardate la figura che inserisco qui sotto.
Prendiamo un punto, posto sul battistrada nel piano di simmetria della ruota.
Nell’avvicinarsi al punto di contatto A con il terreno, questo punto tenderà a muoversi, relativamente al centro della ruota, secondo la direzione di V e quindi, ad uscire dal piano medio della ruota. Quando entra in contatto col suolo, e fino al punto B, la sua velocità (relativa al centro ruota) ha la direzione di V. Quando raggiunge B, le forze di richiamo verso il piano di simmetria sono tali da farlo deviare, costringendolo a strisciare sul terreno. Questo strisciamento prosegue per tutta la restante parte di contatto col suolo, fino a C.
Quindi, possiamo suddividere la zona di contatto del battistrada col suolo in due parti: una prima zona (da A a B) in cui NON si ha strisciamento e una seconda zona (da B a C) in cui SI HA strisciamento.
Questa zona è tanto più grande quanto maggiore è l’angolo di deriva (guardate, nella seconda parte di questo disegno qui sotto, come varia la zona di strisciamento in funzione dell’angolo di deriva: si parte da un angolo di deriva di 8 gradi per arrivare a 1 grado: si vede che la zona di strisciamento si riduce).
Fuoco o non fuoco, noi andiamo avanti (NOI TIREREMO DIRITTO....) anche se piano piano in modo che capiate bene questi argomenti.
Dopo aver chiarito bene cosa sia l’angolo di deriva del pneumatico, vediamo le forze scambiate tra pneus e strada in direzione trasversale.
Se il pneus si muove con un certo angolo di deriva, la forma della zona di contatto risulta notevolmente distorta.
Guardate la figura che inserisco qui sotto.
Prendiamo un punto, posto sul battistrada nel piano di simmetria della ruota.
Nell’avvicinarsi al punto di contatto A con il terreno, questo punto tenderà a muoversi, relativamente al centro della ruota, secondo la direzione di V e quindi, ad uscire dal piano medio della ruota. Quando entra in contatto col suolo, e fino al punto B, la sua velocità (relativa al centro ruota) ha la direzione di V. Quando raggiunge B, le forze di richiamo verso il piano di simmetria sono tali da farlo deviare, costringendolo a strisciare sul terreno. Questo strisciamento prosegue per tutta la restante parte di contatto col suolo, fino a C.
Quindi, possiamo suddividere la zona di contatto del battistrada col suolo in due parti: una prima zona (da A a B) in cui NON si ha strisciamento e una seconda zona (da B a C) in cui SI HA strisciamento.
Questa zona è tanto più grande quanto maggiore è l’angolo di deriva (guardate, nella seconda parte di questo disegno qui sotto, come varia la zona di strisciamento in funzione dell’angolo di deriva: si parte da un angolo di deriva di 8 gradi per arrivare a 1 grado: si vede che la zona di strisciamento si riduce).
Allegati
Allora, se avete capito tutto,
Andiamo avanti.
La risultante Fy della distribuzione delle pressioni tangenziali, che si indicano con la lettera greca tau (τ) NON è applicata al centro dell’orma di contatto. Bensì in un punto a distanza t dal centro dell’orma di contatto, verso IL DIETRO (in posizione arretrata). Guardate il disegno che allego e capirete: riporta i grafici della distribuzione della forza verticale (il secondo grafico) e della forza laterale Fy. In ascisse è riportata la corda dell’area di contatto. Vedete che la forza laterale Fy NON è applicata al centro dell’orma ma è spostata indietro a distanza t dal centro stesso?
Andiamo avanti.
La risultante Fy della distribuzione delle pressioni tangenziali, che si indicano con la lettera greca tau (τ) NON è applicata al centro dell’orma di contatto. Bensì in un punto a distanza t dal centro dell’orma di contatto, verso IL DIETRO (in posizione arretrata). Guardate il disegno che allego e capirete: riporta i grafici della distribuzione della forza verticale (il secondo grafico) e della forza laterale Fy. In ascisse è riportata la corda dell’area di contatto. Vedete che la forza laterale Fy NON è applicata al centro dell’orma ma è spostata indietro a distanza t dal centro stesso?
Allegati
In conseguenza di ciò, nasce un momento che risulta essere definito come il prodotto della forza Fy moltiplicata per il braccio t
Mz = Fy t
Questo momento prende il nome di MOMENTO AUTOALLINEANTE perché tende a riportare il piano di simmetria della ruota nella direzione della velocità V.
Insomma, tende a fare “riallineare” la ruota. Insomma, quando nasce un angolo di deriva α nasce contemporaneamente una distribuzione di sforzi tangenziali tale da generare una forza trasversale Fy che, spostata rispetto al centro dell’orma di contatto, genera a sua volta un momento autoallineante.
L’andamento del momento autoallineante, al variare del carico verticale (peso) e in funzione dell’angolo di deriva α, è riportato nella figura che allego qui sotto
Mz = Fy t
Questo momento prende il nome di MOMENTO AUTOALLINEANTE perché tende a riportare il piano di simmetria della ruota nella direzione della velocità V.
Insomma, tende a fare “riallineare” la ruota. Insomma, quando nasce un angolo di deriva α nasce contemporaneamente una distribuzione di sforzi tangenziali tale da generare una forza trasversale Fy che, spostata rispetto al centro dell’orma di contatto, genera a sua volta un momento autoallineante.
L’andamento del momento autoallineante, al variare del carico verticale (peso) e in funzione dell’angolo di deriva α, è riportato nella figura che allego qui sotto
Allegati
guardando questi grafici mi sembra di capire che il momento allineante (che, in termini di sensazioni mentre si guida, potrei descrivere come pesantezza dello sterzo) per "bassi" angoli di deriva aumenta con l'aumentare della deriva (spannometricamente: mano a mano che mi spingo verso il limite, all'inizio lo sterzo diventa sempre più duro), poi raggiungo un massimo e oltre un certo angolo di deriva il momento allineante cala (appropinquandosi al limite, la deriva aumenta "troppo" e mi sento lo sterzo alleggerirsi) e può anche annullarsi del tutto
però, più carico verticale posso mettere sulla gomma, maggiore è la deriva che posso "sopportare" prima che mi si alleggerisca lo sterzo
EDIT: ovviamente, il tutto supponendo di parlare solo di ruote anteriori
però, più carico verticale posso mettere sulla gomma, maggiore è la deriva che posso "sopportare" prima che mi si alleggerisca lo sterzo
EDIT: ovviamente, il tutto supponendo di parlare solo di ruote anteriori
Diabolik":l68wy3fi ha detto:
Trattandosi di momento allineante immagino che sia percettibile al volante come un appesantimento quando cerco di aumentare l'angolo di sterzata (dal centro verso la direzione desiderata) e un alleggerimento in direzione contraria (verso il centro).
Diabolik":7kh6wf4j ha detto:
ciao
ho poco tempo, al limite continuiamo domani.
molte inesattezze.
prima di tutto: si parla di ruote, anteriori o posteriori non c'è differenza. valgono sempre le stesse regole. tutt'al più, l'unica cosa che cambia è il fatto che davanti hai lo sterzo...ma anche dietro hai deriva (sennò, come faresti a curvare?), Fy e momenti autoallinenanti?
e poi: dove lo vedi "il limite"? il "limite" de che? guarda i valori di angolo di deriva cui corrispondono le curve postate...stiamo parlando di valori bassi...
peraltro, si parla di angolo di deriva, mica di angolo di sterzo....posso avere lo stesso angolo di deriva a differenti angoli di sterzo (ossia col volante girato poco e anche col volante girato tantissimo: l'angolo di deriva NON è l'angolo di sterzo...)
il fatto che lo sterzo diventi "duro" o "molle" non dipende (o non solo, almeno) da "quel" momento autoallinenante...ma pure dal momento autoallinenante generato dai bracci a terra (se ci riferiamo a forze "passive") e dai bracci a centro ruota (quando tiriamo in ballo le forze di trazione)...
ragazzi, stiamo parlando di valori di angolo di deriva di 2 gradi (per il picco massimo) e di 8 gradi (per l'annullarsi del momento)...
si, capisco le tue precisazioni
il mio voleva solo essere un tentativo di interpretare, da un punto di vista di un guidatore qualsiasi con in mano il volante, gli effetti generati dal momento allineante di cui sopra; mi rendo conto che, fatto così in isolamento dagli altri fattori (braccio a terra che dicevi e tutte le altre cose), diventa difficile se non impossibile descrivere effettivamente cosa dovrei sentire sul volante
per quanto riguarda il limite, non avevo idea della significatività degli angoli nell'intervallo dei grafici: non ho mai fatto attenzione a quest otipo di aspetto; buono a sapersi che 8° sono pochi, mi piacerebbe sapere fino a quanto può arrivare prima di sconfinare nella perdita di aderenza
correggimi se sbaglio: all'anteriore, sterzando, avrò sempre una deriva non nulla, mentre al posteriore dipende
il mio voleva solo essere un tentativo di interpretare, da un punto di vista di un guidatore qualsiasi con in mano il volante, gli effetti generati dal momento allineante di cui sopra; mi rendo conto che, fatto così in isolamento dagli altri fattori (braccio a terra che dicevi e tutte le altre cose), diventa difficile se non impossibile descrivere effettivamente cosa dovrei sentire sul volante
per quanto riguarda il limite, non avevo idea della significatività degli angoli nell'intervallo dei grafici: non ho mai fatto attenzione a quest otipo di aspetto; buono a sapersi che 8° sono pochi, mi piacerebbe sapere fino a quanto può arrivare prima di sconfinare nella perdita di aderenza
correggimi se sbaglio: all'anteriore, sterzando, avrò sempre una deriva non nulla, mentre al posteriore dipende
O anocra una volta non ho capito veramente una mazza, o 8 gradi sono tanti: andando un paio di disegni indietro, a 8 gradi la risultante delle forze laterali si avvicina molto al centro della ruota e per questo il momento risultante si riduce molto.Diabolik":1eqwkvc7 ha detto:
Mi viene da pensare che a 8 gradi non essendoci piu' (quasi) il momento autoallineante, alla ruota non gliene freghi piu' nulla se qualcuno le sta imponendo una posizione diversa rispetto alla direzione che sta percorrendo.