La sospensione dell'autoveicolo - approfondimenti

[alfistavero]

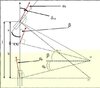
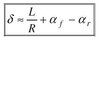Però,

noi abbiamo detto che sia BETA, sia ALFA (cioè l’angolo di deriva posteriore) sono PICCOLI, cioè hanno valori PICCOLI.

Questo significa che:

il seno di BETA, cioè sin(BETA), sarà asintotico a BETA,
il coseno di BETA, cioè cos (BETA), sarà asintotico a 1
la tangente di ALFA, essendo null’altro che il rapporto tra seno e coseno, sarà asintotico al rapporto tra ALFA e 1. Quindi, varrà ALFA.

Siete d’accordo (sono tutte semplificazioni matematiche, nulla di più)?

Bene, allora la formula qui sopra diventerà

b/R – Rβ/R ~ ALFAp

quindi, semplificando R nel secondo termine,

b/R – β ~ ALFAp

che, scritto meglio (copio anche qui), diventa:

 

[alfistavero]

Adesso, possiamo fare lo stesso discorso per l’anteriore, trovando la relazione che ci permette di “collegare” l’angolo di sterzo (DELTA) con gli angoli di deriva anteriore e posteriore.

Evitiamo i conti (se volete divertirvi, fatelo voi per esercizio; sennò credetemi sulla parola) e passiamo subito al risultato.
Anche in questo caso, copio la formula così la scriviamo bene e non ci sono fraintendimenti

 

[alfistavero]

queste due formule, che adesso andiamo a vedere, devono essere stampate nella vostra testa

 

[alfistavero]

la prima dice che l'assetto, cioè quanto il muso della macchina punta all'interno o all'esterno della curva, dipende SOLO da (una costante, che è b/R e da) l'angolo di deriva del posteriore. ossia, il fatto che la macchina "assetti", cioè si disponga poco o tanto "di traverso" (in condizioni stabilizzate!!!!) dipende solo DAL POSTERIORE. quindi, potete fare tutto quello che volete al vostro avantreno (per esempio, cambiare le gomme, cambiare la convergenza, il camber o quel ****Edit da STAFF: alla prossima account sospeso! che volete voi) ma il comportamento della vostra macchina NON cambierà per niente. dovete intervenire sul posteriore.
ossia, se durante la curva la vostra macchina si dispone tanto o poco di traverso, cioè rivolge il muso (durante tutto l'arco della curva) dentro o fuori la traiettoria, verso il centro della traiettoria o verso l'esterno, questo dipende SOLO dal posteriore.

e questo non mi sembra poco.

la seconda mi dice che la quantità di sterzo necessaria per compiere la curva, cioè "quanto" devo girare il volante, dipende (a meno, anche qui da un coefficiente) dal rapporto tra avantreno e retrotreno.

pensateci

andiamo avanti domani

 

[Diabolik]

“collegare” l’angolo di sterzo (DELTA) con gli angoli di deriva anteriore e posteriore.

fico

dice che se deriva anteriore = deriva posteriore io devo sterzare "normale"
mentre se davanti ho più deriva devo sterzare di più
mentre se dietro ho più deriva devo sterzare di meno

.... chissà a questo punto cosa potremo dire su neutro-sotto-sovrasterzo...

 

[bigno72]

Le mie considerazioni dopo gli utlimi post (ho anche un tarlo, che espongo dopo):

Se faccio aumentare la deriva posteriore, A PARITA' DI RAGGIO, cambia l'angolo di assetto, ma cambia anche l'angolo di sterzo (devo "aprire").
Diminuisce la deriva anteriore, o la variazione di angolo di sterzo sara' sempre tale da rendere vera la seconda equazione al variare di ALFAp ma tenendo fisso ALFAa?.

Se faccio aumentare la deriva anteriore, sempre a parita' di raggio, cambia l'angolo di sterzo (devo chiudere).
Se e' vero che toccando l'anteriore non cambia l'angolo di assetto, vuol dire che variando la deriva anteriore, la conseguente variazione di angolo volante sara' tale da non far variare la deriva posteriore.


Il mio tarlo:
riesco a seguire la parte trigonometrica perche' ALFAp e BETA nel disegno sono stati riportati sul vertice O.
Ma sbaglio, o manca il passaggio che dimostra che quei due angoli (quelli indicati sul vertice O) sono proprio ALFAp e BETA?


Sono pronto... :sadomaso)

 

[Diabolik]

sono proprio ALFAp e BETA?

devi andare a ricontrollare i criteri di congruenza degli angoli e poi vedrai che sono proprio loro, per come il disegno è stato costruito (okkio a notare bene dove stanno gli angoli retti, che sono tali proprio per costruzione)

 

[rossomandello]

Il mio tarlo:
riesco a seguire la parte trigonometrica perche' ALFAp e BETA nel disegno sono stati riportati sul vertice O.
Ma sbaglio, o manca il passaggio che dimostra che quei due angoli (quelli indicati sul vertice O) sono proprio ALFAp e BETA?

Bigno, semplicemente gli angoli formati da rette (o segmenti) a due a due ortogonali sono uguali; in questo caso il segmento tratteggiato è ortogonale all'asse del veicolo, mentre il segm O-CG è ortogonale alla velocità del baricentro (CG), quindi l'angolo indicato in O è proprio BETA.

Stessa cosa per ALFAp.

 

[bigno72]

Cioe' mi stai dicendo che gli angoli che ho indicato in verde qui:


sono angoli retti? :?:

Meraviglie della non-standardizzazione delle risoluzioni :lol:

 

[alfistavero]

Le mie considerazioni ........................Sono pronto... :sadomaso)

conserva le considerazioni per dopo: non abbiamo ancora finito...

magari domani pomeriggio (tardi) proseguiamo

sennò, giovedi (sempre pomeriggio tardi); o venerdì mattina

 

[Diabolik]

sono angoli retti? :?:

yesssssssssssss

 

[rossomandello]

sono angoli retti? :?:

yesssssssssssss

Sono sempre gli informatici a fare casini... :lol:

 

[thranduil]

rinfrescati i triangoli simili, che forse fai prima: possiamo costruire dei triangoli rettangoli con un angolo in comune, che è quello formato dalla direzione della ruota post (la freccia rossa) con l'orizzontale da O :OK)

 

[alfistavero]

Cioe' mi stai dicendo che gli angoli che ho indicato in verde qui:


sono angoli retti? :?:

Meraviglie della non-standardizzazione delle risoluzioni :lol:

MINKIA, Bigno :wall) :wall) :wall) :wall)

lo sono per DEFINIZIONE!!!!!!!!!!!!!!!!

gli atti di moto devono essere perpendicolari alle rette, quindi le rette devono essere perpendicolari ai vettori velocità :mad2) :mad2)

 

[thranduil]

sono angoli retti? :?:

yesssssssssssss

per definizione: abbiamo trovato O proprio portando le perpendicolari alle velocità "reali" delle ruote :nod)

 

[alfistavero]

e il bello deve ancora venire :nod) :nod)

 

[bigno72]

per definizione: abbiamo trovato O proprio portando le perpendicolari alle velocità "reali" delle ruote :nod)

E dire che questa cosa ce l'avevo chiara... :wall)

 

[rossomandello]

la seconda mi dice che la quantità di sterzo necessaria per compiere la curva, cioè "quanto" devo girare il volante, dipende (a meno, anche qui da un coefficiente) dal rapporto tra avantreno e retrotreno.

Un paio di riflessioni ad alta voce:
- In condizioni cinematiche, l'angolo di sterzo dipende solo da parametri geometrici (e mi sembra ragionevole...)
- per opportuni valori di deriva anteriore e posteriore potrei avere che, in condizioni stabilizzate, percorro una curva di raggio R con angolo di sterzo nullo (a ruote dritte...)
- al limite, se deriva post >> deriva anteriore, per percorrere la stessa curva di raggio R mi serve un angolo di sterzo negativo (sterzo verso l'esterno) e anche l'angolo di assetto sarà negativo (macchina che punta verso l'esterno). Ma in questo caso siamo fuori dall'ipotesi iniziale di angoli di deriva piccoli...quindi le approx che abbiamo fatto potrebbero non essere più valide.

Giusto?

Direi che fin qui abbiamo fatto solo considerazioni geometriche, senza introdurre forze e senza parlare di pneumatici ('la Bibbia' direbbe che abbiamo scritto le equazioni di congruenza della bicicletta...)

 

[MAD147]

..........
Noi non abbiamo poteri admin estesi al punto da abilitare e revocare permessi. Parlane con lo staff. :nod)

ehh, vabbè.
vorrà dire che NON vi aiuterò per Balocco a Maggio....

Non possiamo, mica non vogliamo... :asd)
Ripeto, parlane con lo staff. Piccolo trucco: se minacci il presidente di pisciargli sulla gta ottieni di sicuro il premesso di leggere pure la sua password del bancomat... :lol: :lol: :lol: :lol:

 

[bigno72]

percorro una curva di raggio R con angolo di sterzo nullo (a ruote dritte...)

Come Alfistavero con la Rover 214 :ignore)

- al limite, se deriva post >> deriva anteriore, per percorrere la stessa curva di raggio R mi serve un angolo di sterzo negativo (sterzo verso l'esterno) e anche l'angolo di assetto sarà negativo (macchina che punta verso l'esterno).

Non mi torna: se l'angolo di assetto e' negativo la macchina sta puntando verso l'interno.
E questo torna anche con la deriva post>> di quella anteriore.

'la Bibbia' direbbe che abbiamo scritto le equazioni di congruenza della bicicletta...

Si, lo dice....
OPS, avevo detto che non l'avrei piu' guardata!
Ma stamattina non avevo nulla da leggere... :cesso) :crepap)