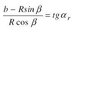Allora,
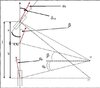
Vediamo, mediante un po’ di trigonometria, di mettere in relazione l’angolo di assetto (BETA, β) e l’angolo di sterzo (DELTA, ) con gli angoli di deriva (ALFA, α rispettivamente ALFAa anteriore e ALFAp posteriore)
Se guardate la figura, vedrete che in pratica questo significa che devo prendere una parte del semipasso posteriore b.
Dopo lunga discussione con Bigno, abbiamo anche visto che commettiamo un errore minimo a considerare R come il segmento O-CG e anche il segmento O-centro ruota posteriore. L’errore sarà minimo.
Quindi (vi scrivo α come ALFA, β come BETA etc, così evitiamo errori di scrittura cisto che è difficile aggiungere lettere greche in questi messaggi),
R sin (ALFAp) = b – R sin (BETA)
Il perchè mi sembra chiaro: R sin (ALFAp) è quel “pezzo” di segmento che va dal centro ruota posteriore a CG, quindi un pezzo del semipasso posteriore b.
E poi (questa è più facile se guardate la figura):
R cos (ALFAp) = R cos (BETA)
Quindi, diventa (copio un pezzo di formula così lo leggete meglio):