La sospensione dell'autoveicolo - approfondimenti
- Autore discussione yugs
- Data d'inizio
Andiamo avanti un po’. Riconsideriamo il nostro disegno, che per vostra comodità vi ripropongo qui.
Allora, ieri abbiamo detto due cose fondamentali.
La prima: consideriamo il modello “a bicicletta”, nel quale vedremo (oltre alle condizioni cinematiche) soprattutto le condizioni dinamiche, cioè quelle condizioni che si generano quando sto viaggiando su strada realmente. Ossia, anche, quando la mia velocità è diversa da ZERO (o da un valore mooooolto piccolo). In queste condizioni, si generano FORZE. In particolare, nel nostro caso, quando percorriamo una curva, si genera un angolo di deriva che genera, appunto, una forza trasversale.
La seconda: considereremo solo quella zona di “lavoro” del pneumatico in cui il rapporto tra la forza trasversale Fy espressa dal pneumatico e l’angolo di deriva α che la genera è una costante (che, guarda caso, è la nostra rigidezza di deriva).
Cosa significa questo?
In pratica, significa che mi tengo su valori di deriva α dell’ordine dei 3-5 gradi (se considero un pneumatico “medio”)
Soprattutto, però: MI TENGO IN CONDIZIONI STABILIZZATE
Ossia, percorro la mia curva a velocità COSTANTE. Questo significa, in pratica, evitare che, durante la percorrenza della curva, si generino accelerazioni o frenate che provocano variazioni di carico tra davanti e dietro; le quali, comporterebbero poi la necessità di agire sullo sterzo per mantenere la macchina sulla traiettoria (o, se non agisco sullo sterzo, una variazione di traiettoria…).
Questo significa, in pratica, che mi tengo su valori di accelerazione trasversale (che, se ricordate, abbiamo chiamato Ay) dell’ordine di 0,4 g.
Volete sapere cosa vuol dire stare su accelerazioni trasversali di 0,4g, che corrispondono a circa 4 m/sec2 ?
Ve lo dico io:
prendiamo una curva di raggio 100 metri. Se la percorrete a 70 Km/h, siete già a quasi 0,4g!!!! Una curva di 100 metri!!!!
Tanto per darvi un’altra idea. Quanto saranno grandi le rotonde che incontrate sulle strade statali? Boh, diciamo tra i 10 e i 20 metri? Diciamo 20 metri. Bene: su una rotonda di 20 metri (di RAGGIO!!!!! Che è già tantissimo), se viaggiate a 40 Km/h, siete a 0,6g!!!
Sempre in condizioni stabilizzate, eh…perché se poi muovete lo sterzo, magari “a chiudere”, andate anche oltre….
Ok? Ci siamo?
Bene, andiamo avanti.
Allora, la mia “bicicletta” starà percorrendo una curva a velocità costante. Una curva di raggio R.
E’ in questa condizione che ho fatto la “foto” alla mia “bici”…e questa foto è il disegno che ho postato ieri!!
E che ripropongo oggi
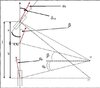
Andiamolo un po’ a vedere e cerchiamo di capire il significato delle sigle e dei vettori.
Allora, partiamo dalla ruota anteriore.
Con la lettera greca DELTA () ho indicato l’ANGOLO DI STERZO. Anzi, ho proprio scritto DELTAvol, lo vedete? Questo è proprio l’angolo di cui ruota la mia ruota davanti quando giro il volante. Giro il volante e le ruote (LA ruotA, nel caso della mia bicicletta) girano. Ecco, DELTA è proprio l’angolo che voi vedete.
Magari ve ne siete già accorti, altrimenti ve lo dico io: è chiaro che voi ruotate il volante di un angolo maggiore rispetto all’angolo di cui ruotano le ruote anteriori. Quindi, questo significa il cinematismo che collega il volante alle ruote ha un suo RAPPORTO DI DEMOLTIPLICAZIONE. Significa, quindi, che c’è un rapporto di trasmissione. Bene, questo rapporto viene indicato con la lettera greca TAU (τ) e vale TAU = DELTAvol/DELTAruote. Attenti, in questa notazione DELTAvol NON è il DELTAvol riportato nella figura qui sotto. questo perché ho sbagliato a fare il disegno (quando l’ho fatto stavo pensando ad altro e siccome l’età è quella che è….vi prego di scusarmi). Comunque, DELTAvol è l’angolo di cui ruota il volante quando lo giro. DELTA (e basta; o anche per farvi capire DELTAruote) è l’angolo di cui ruotano le ruote (quello che in figura è indicato con DELTAvol…).
Allora, è inutile che vi dica che quanto più il valore di TAU è BASSO, tanto più lo sterzo è DIRETTO; e, al contrario, tanto più alto è il valore di TAU, tanto meno diretto sarà lo sterzo.
Le macchine di intonazione sportiva hanno sterzi che tendono ad essere diretti….i pullmann hanno sterzi che tendono ad essere demoltiplicati, tanto per fare degli esempi scemi…..poi ci sarebbero altre 5000 considerazioni che qui tralascio….
In più, tanto per dare dei valori, così comprendete un po’ meglio, vi dico che, ai tempi in cui è uscita la 156, la media dei valori di TAU delle concorrenti della 156 stava nell’intorno di 17. la 156 è uscita con 13!! (e infatti l’audi ci è poi venuta dietro….e ci è venuta dietro in altre cose, con la TT…con tutto quello che ne è conseguito….più avanti avremo sicuramente modo di capire cosa è successo alla TT)
Per adesso, lasciamo stare particolari tipi di sterzo a rapporto variabile (tipo l’Active steering della BMW o quello della Lexus, etc)….
ATTENTI BENE!!!! riguardatevi il disegno: NON confondete l’angolo di sterzo (DELTA) con l’angolo di deriva ALFA (α). Nel disegno ho indicato un ALFAa, cioè anteriore, e un ALFAp, cioè posteriore, per la ruota posteriore perché anche la ruota posteriore, siccome sto sterzando in condizioni reali (e non cinematiche) è in deriva. Lo dico, ma spero che l’abbiate capito lo stesso:
Quando vado in giro con la macchina, e faccio una curva, hanno un angolo di deriva sia le ruote anteriori sia le ruote posteriori.
Ma torniamo al disegno.
Dicevamo dell’angolo di deriva.
Mi permetto di rammentarvi che cos’è l’angolo di deriva: è l’angolo formato dalla velocità (di traslazione del pneumatico) con l’asse (o il piano verticale) del pneus stesso.
Guardate la freccia rossa della ruota davanti (ma anche di quella dietro). L’angolo formato dalla velocità (freccia rossa) con l’asse della ruota E’ l’angolo di deriva. E considerate pure, guardando la ruota anteriore, che angolo di deriva e angolo sterzo NON sono la stessa cosa!!!! Guardatelo sul disegno!!!!
L’angoo sterzo, in queste condizioni, è SEMPRE maggiore dell’angolo di deriva.
Poi, cosa c’è?
C’è un’altra freccia rossa, posta nel baricentro (CG), che genera un angolo con l’asse vettura (della bicicletta). Allora, l’angolo, che indico con BETA (β) è l’angolo di ASSETTO della bici (della vettura). Attenti bene a non confonderlo (pure questo!!!) con l’assetto come lo conoscete voi….”quello” (di assetto) è l’assetto della vettura, ossia la posizione statica della vettura rispetto alla linea di terra (quello che comunemente viene indicata come “l’altezza” della macchina….infatti, una macchina “assettata” è, nel gergo comune, una macchina “abbassata”, con l’assetto, appunto…).
Qui, l’assetto è un’altra cosa: l’angolo di assetto è l’angolo formato dalla velocità (del baricentro!!!!), indicato dalla freccia rossa, con l’asse della vettura (che nel mio caso è la bicicletta).
Se volete, se vi è più facile capirla come ve la dico adesso, l’angolo di assetto è……l’angolo di deriva del baricentro!!!!
Guardate la figura: l’angolo di assetto BETA che ho disegnato è POSITIVO, perché è rivolto all’interno della curva.
Immaginate una macchina che sta facendo una curva “di traverso”, in derapata. In quel caso, pensate a come può essere l’angolo di assetto di quella vettura. L’angolo di assetto sarà rivolto verso l’esterno della curva perché il vettore velocità (rosso) è diretto verso l’esterno, fuori (e infatti la mia macchina è di traverso…) mentre l’asse di mezzeria della macchina “guarda” verso l’interno. Bene: tenete ben presente queste considerazioni, perché ci serviranno tra poco.
Poi, che c’è? C’è l’angolo di deriva della ruota posteriore, di cui abbiamo già parlato.
E c’è il passo, indicato con l minuscolo e i due semipassi anteriore e posteriore (a e b) che sono, in pratica la distanza del baricentro rispettivamente dall’asse anteriore e dall’asse posteriore (guardate la figura). Chiaro che, se ho il baricentro (CG) spostato in avanti a sarà minore di b; e viceversa.
Infine, c’è il centro di istantanea rotazione O. Invero ho anche disegnato O’ perché ci servirà. E c’è, naturalmente, il raggio della curva R.
Se avete capito fin qui…..
Venghino signori, si va a cominciare…..
Allora, ieri abbiamo detto due cose fondamentali.
La prima: consideriamo il modello “a bicicletta”, nel quale vedremo (oltre alle condizioni cinematiche) soprattutto le condizioni dinamiche, cioè quelle condizioni che si generano quando sto viaggiando su strada realmente. Ossia, anche, quando la mia velocità è diversa da ZERO (o da un valore mooooolto piccolo). In queste condizioni, si generano FORZE. In particolare, nel nostro caso, quando percorriamo una curva, si genera un angolo di deriva che genera, appunto, una forza trasversale.
La seconda: considereremo solo quella zona di “lavoro” del pneumatico in cui il rapporto tra la forza trasversale Fy espressa dal pneumatico e l’angolo di deriva α che la genera è una costante (che, guarda caso, è la nostra rigidezza di deriva).
Cosa significa questo?
In pratica, significa che mi tengo su valori di deriva α dell’ordine dei 3-5 gradi (se considero un pneumatico “medio”)
Soprattutto, però: MI TENGO IN CONDIZIONI STABILIZZATE
Ossia, percorro la mia curva a velocità COSTANTE. Questo significa, in pratica, evitare che, durante la percorrenza della curva, si generino accelerazioni o frenate che provocano variazioni di carico tra davanti e dietro; le quali, comporterebbero poi la necessità di agire sullo sterzo per mantenere la macchina sulla traiettoria (o, se non agisco sullo sterzo, una variazione di traiettoria…).
Questo significa, in pratica, che mi tengo su valori di accelerazione trasversale (che, se ricordate, abbiamo chiamato Ay) dell’ordine di 0,4 g.
Volete sapere cosa vuol dire stare su accelerazioni trasversali di 0,4g, che corrispondono a circa 4 m/sec2 ?
Ve lo dico io:
prendiamo una curva di raggio 100 metri. Se la percorrete a 70 Km/h, siete già a quasi 0,4g!!!! Una curva di 100 metri!!!!
Tanto per darvi un’altra idea. Quanto saranno grandi le rotonde che incontrate sulle strade statali? Boh, diciamo tra i 10 e i 20 metri? Diciamo 20 metri. Bene: su una rotonda di 20 metri (di RAGGIO!!!!! Che è già tantissimo), se viaggiate a 40 Km/h, siete a 0,6g!!!
Sempre in condizioni stabilizzate, eh…perché se poi muovete lo sterzo, magari “a chiudere”, andate anche oltre….
Ok? Ci siamo?
Bene, andiamo avanti.
Allora, la mia “bicicletta” starà percorrendo una curva a velocità costante. Una curva di raggio R.
E’ in questa condizione che ho fatto la “foto” alla mia “bici”…e questa foto è il disegno che ho postato ieri!!
E che ripropongo oggi
Andiamolo un po’ a vedere e cerchiamo di capire il significato delle sigle e dei vettori.
Allora, partiamo dalla ruota anteriore.
Con la lettera greca DELTA () ho indicato l’ANGOLO DI STERZO. Anzi, ho proprio scritto DELTAvol, lo vedete? Questo è proprio l’angolo di cui ruota la mia ruota davanti quando giro il volante. Giro il volante e le ruote (LA ruotA, nel caso della mia bicicletta) girano. Ecco, DELTA è proprio l’angolo che voi vedete.
Magari ve ne siete già accorti, altrimenti ve lo dico io: è chiaro che voi ruotate il volante di un angolo maggiore rispetto all’angolo di cui ruotano le ruote anteriori. Quindi, questo significa il cinematismo che collega il volante alle ruote ha un suo RAPPORTO DI DEMOLTIPLICAZIONE. Significa, quindi, che c’è un rapporto di trasmissione. Bene, questo rapporto viene indicato con la lettera greca TAU (τ) e vale TAU = DELTAvol/DELTAruote. Attenti, in questa notazione DELTAvol NON è il DELTAvol riportato nella figura qui sotto. questo perché ho sbagliato a fare il disegno (quando l’ho fatto stavo pensando ad altro e siccome l’età è quella che è….vi prego di scusarmi). Comunque, DELTAvol è l’angolo di cui ruota il volante quando lo giro. DELTA (e basta; o anche per farvi capire DELTAruote) è l’angolo di cui ruotano le ruote (quello che in figura è indicato con DELTAvol…).
Allora, è inutile che vi dica che quanto più il valore di TAU è BASSO, tanto più lo sterzo è DIRETTO; e, al contrario, tanto più alto è il valore di TAU, tanto meno diretto sarà lo sterzo.
Le macchine di intonazione sportiva hanno sterzi che tendono ad essere diretti….i pullmann hanno sterzi che tendono ad essere demoltiplicati, tanto per fare degli esempi scemi…..poi ci sarebbero altre 5000 considerazioni che qui tralascio….
In più, tanto per dare dei valori, così comprendete un po’ meglio, vi dico che, ai tempi in cui è uscita la 156, la media dei valori di TAU delle concorrenti della 156 stava nell’intorno di 17. la 156 è uscita con 13!! (e infatti l’audi ci è poi venuta dietro….e ci è venuta dietro in altre cose, con la TT…con tutto quello che ne è conseguito….più avanti avremo sicuramente modo di capire cosa è successo alla TT)
Per adesso, lasciamo stare particolari tipi di sterzo a rapporto variabile (tipo l’Active steering della BMW o quello della Lexus, etc)….
ATTENTI BENE!!!! riguardatevi il disegno: NON confondete l’angolo di sterzo (DELTA) con l’angolo di deriva ALFA (α). Nel disegno ho indicato un ALFAa, cioè anteriore, e un ALFAp, cioè posteriore, per la ruota posteriore perché anche la ruota posteriore, siccome sto sterzando in condizioni reali (e non cinematiche) è in deriva. Lo dico, ma spero che l’abbiate capito lo stesso:
Quando vado in giro con la macchina, e faccio una curva, hanno un angolo di deriva sia le ruote anteriori sia le ruote posteriori.
Ma torniamo al disegno.
Dicevamo dell’angolo di deriva.
Mi permetto di rammentarvi che cos’è l’angolo di deriva: è l’angolo formato dalla velocità (di traslazione del pneumatico) con l’asse (o il piano verticale) del pneus stesso.
Guardate la freccia rossa della ruota davanti (ma anche di quella dietro). L’angolo formato dalla velocità (freccia rossa) con l’asse della ruota E’ l’angolo di deriva. E considerate pure, guardando la ruota anteriore, che angolo di deriva e angolo sterzo NON sono la stessa cosa!!!! Guardatelo sul disegno!!!!
L’angoo sterzo, in queste condizioni, è SEMPRE maggiore dell’angolo di deriva.
Poi, cosa c’è?
C’è un’altra freccia rossa, posta nel baricentro (CG), che genera un angolo con l’asse vettura (della bicicletta). Allora, l’angolo, che indico con BETA (β) è l’angolo di ASSETTO della bici (della vettura). Attenti bene a non confonderlo (pure questo!!!) con l’assetto come lo conoscete voi….”quello” (di assetto) è l’assetto della vettura, ossia la posizione statica della vettura rispetto alla linea di terra (quello che comunemente viene indicata come “l’altezza” della macchina….infatti, una macchina “assettata” è, nel gergo comune, una macchina “abbassata”, con l’assetto, appunto…).
Qui, l’assetto è un’altra cosa: l’angolo di assetto è l’angolo formato dalla velocità (del baricentro!!!!), indicato dalla freccia rossa, con l’asse della vettura (che nel mio caso è la bicicletta).
Se volete, se vi è più facile capirla come ve la dico adesso, l’angolo di assetto è……l’angolo di deriva del baricentro!!!!
Guardate la figura: l’angolo di assetto BETA che ho disegnato è POSITIVO, perché è rivolto all’interno della curva.
Immaginate una macchina che sta facendo una curva “di traverso”, in derapata. In quel caso, pensate a come può essere l’angolo di assetto di quella vettura. L’angolo di assetto sarà rivolto verso l’esterno della curva perché il vettore velocità (rosso) è diretto verso l’esterno, fuori (e infatti la mia macchina è di traverso…) mentre l’asse di mezzeria della macchina “guarda” verso l’interno. Bene: tenete ben presente queste considerazioni, perché ci serviranno tra poco.
Poi, che c’è? C’è l’angolo di deriva della ruota posteriore, di cui abbiamo già parlato.
E c’è il passo, indicato con l minuscolo e i due semipassi anteriore e posteriore (a e b) che sono, in pratica la distanza del baricentro rispettivamente dall’asse anteriore e dall’asse posteriore (guardate la figura). Chiaro che, se ho il baricentro (CG) spostato in avanti a sarà minore di b; e viceversa.
Infine, c’è il centro di istantanea rotazione O. Invero ho anche disegnato O’ perché ci servirà. E c’è, naturalmente, il raggio della curva R.
Se avete capito fin qui…..
Venghino signori, si va a cominciare…..
Allegati
rossomandello":1y0z4gro ha detto:Non oso immaginare la lunghezza del post quando spiegherai la formula alla base di tutto...
beh, vedremo di farla semplice.....
oppure di spezzare il post in tanti post...ini :lol:
rossomandello":1hr3lyya ha detto:Non oso immaginare la lunghezza del post quando spiegherai la formula alla base di tutto...
la MADRE di tutte le formule, che serve per capire TUTTO :lol: :X)
chissà perchè sto disegnino mi sembrava di averlo già visto.... :asd)
solo che ora coi commenti (specialmente col commento che spiega l'idea del modello, ovvero prendere la macchina e ignorare rollio e beccheggio) capisco un sacco di cose in più
solo che ora coi commenti (specialmente col commento che spiega l'idea del modello, ovvero prendere la macchina e ignorare rollio e beccheggio) capisco un sacco di cose in più
Diabolik":1jdneli2 ha detto:
in tutti i libri di dinamica del veicolo
più o meno ben fatto
più o meno chiaro
più o meno completo...
.......ma l'è semper quel
Diabolik":1cwloqh5 ha detto:
spero che mi riconoscerai il merito di aver fatto un disegno PIU' chiaro, completo, esaustivo.
spero
Sarebbe la perpendicolare all'asse del veicolo passante per O?alfistavero":3h53kuk1 ha detto:
Oppure il segmento che congiunge O con CG?
Direi di si, anche se ci sono ancora molte altre cose su quel disegno... :asd)
Ma quello che hai descritto finora e' chiarissimo (l'angolo di assetto e' forse quello meno intuitivo, ma finche' si resta sul disegno e' chiarissimo).
bigno72":3p61h04p ha detto:
:wall) :wall) :wall) :wall) :wall) :wall) :wall) :wall) :wall) :wall) :wall)
:mad2) :mad2) :mad2) :mad2) :mad2) :mad2) :mad2) :mad2) :mad2)
:swear) :swear) :swear) :swear) :swear) :swear) :swear) :swear) :swear)
bigno72":3p61h04p ha detto:
direi di no. :nono)
:wall)
Belin ma non era una delle due possibilita' che ho scritto??? :scratch)
Lo scritta 2 minuti dopo aver postato il messaggio, modificandolo, ma tu non eri connesso, quindi non dovresti aver letto per errore la prima versione dove ancora non c'era la seconda ipotesi.
Lo scritta 2 minuti dopo aver postato il messaggio, modificandolo, ma tu non eri connesso, quindi non dovresti aver letto per errore la prima versione dove ancora non c'era la seconda ipotesi.
bigno72":ufb0uekw ha detto:
sarebbe come se scrivessi: ho capito, i freni servono per rallentare. o per accelerare.
se scrivi così, dimostri di non avere capito un belino; scusa.
sei d'accordo?
ho ragione o dico bene?
per esempio, se guardi i segmenti tratteggiati, vedrai che il raggio R è quello che congiunge O' alla ruota posteriore.
il segmento che congiunge O' alla ruota anteriore, invece, è solo un segmento che passa per il centro di istantanea rotazione O'.
questo è il caso cinematico.
ma lo lasciavo lì senza dire nulla perchè prima devo dire ancora qualcosa.
però ti serve come esempio. lo vedi che i due segmenti sono di lunghezza differente?
il segmento che congiunge O' alla ruota anteriore, invece, è solo un segmento che passa per il centro di istantanea rotazione O'.
questo è il caso cinematico.
ma lo lasciavo lì senza dire nulla perchè prima devo dire ancora qualcosa.
però ti serve come esempio. lo vedi che i due segmenti sono di lunghezza differente?
Non sono troppo daccordo: la differenza tra le mie due ipotesi e' PER ME CHE NON CAPISCO ANCORA UN BELINO sottile!alfistavero":tf2mtocr ha detto:
Perche' devo considerare uno e non l'altro?
Mi va benissimo anche la risposta "perche' te lo dico io e devi seguire il mio ragionamento".
Ma resta il fatto che non avevo elementi per individuare quale dei due fosse quello corretto.
Lo vedo si che son diversi.alfistavero":2tn7sada ha detto:
E potrei anche dire che uno e' il raggio della curva percorsa dalla ruota posteriore, e l'altro quello della ruota anteriore.
Tu mi stai dicendo che IL raggio e' quello posteriore. OK, vorrei capire perche' (ma qui aspetto, come lasci intendere di dover fare
)