andiamo avanti
per semplicictà, proporrei di dividere le sospensioni in ANTERIORI e POSTERIORI. così, magari facciamo meno casini
allora, abbiamo visto che ci sono delle funzioni che la sospensione deve svolgere. e il progettista deve, sempre e in ogni caso, progettare delle sospensioni che tengano conto di queste esigenze funzionali (sennò, che cavolo di progettista sarebbe?). e può farlo con grande libertà (almeno teoricamente). unico vincolo, ripeto ancora perchè vi entri in mente, rimane il soddifacimento delle 3 funzioni principali. però questo non basta.
bisogna soddisfare le 3 funzioni principali ma bisogna soddisfarle
1 nella maniera più affidabile (sennò poi ci troviamo dei cagacazzi come voi che rompono le balle perchè ogni volta che saltano da un ponte sentono gnek gnek del tampone di fine corsa

)
2 nella maniera più semplice per la fabbricazione (sennò come farebbe il costruttore a guadagnarci


)
3 con il minimo peso (sennò, i soliti cagacazzi di cui sopra, che sareste voi, si lamentano perchè la macchina pesa troppo), con il minimo costo (sennò come fanno a darci l'aumento di stipendio?), con il minimo ingombro (sennò facciamo un carroarmato, non una macchina)
4 in modo da non penalizzare gli organi a cui ci si attacca (la scocca) e
5 offrendo il massimo delle prestazioni tecniche richieste dalla vettura che si sta progettando
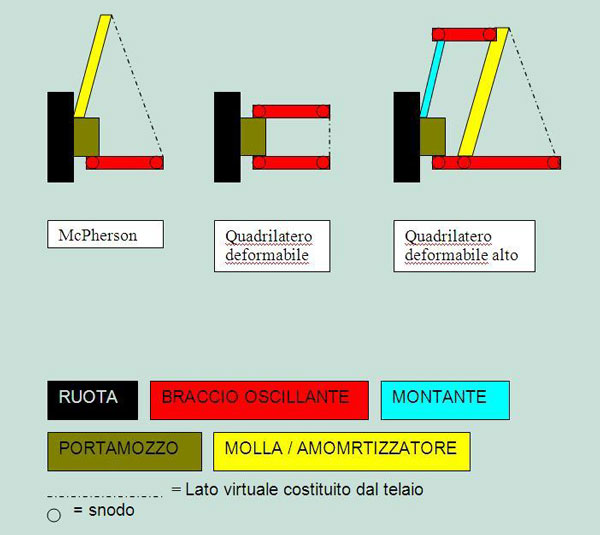
ora, i tipi di sospensione ANTERIORE che si sono salvati a questa serie di VINCOLI (ho fatto apposta ad usare questa parola) importanti e che li soddisfano al meglio, almeno allo stato attuale delle cose, sono 2
a) sospensione a quadrilatero (e qui ci mettiamo anche il quadrilatero alto della 156/147, perchè tecnicamente concettualmente analoga)
b) Mc Pherson
ora, questo non significa che non possano essere adottati differenti schemi sospensivi per l'avantreno: per esempio, moltissime fuoristrada, di quelle vere (mica quelle cagate di SUV), hanno un bel ponte rigido, di cui parleremo più avanti (ricordatemelo, se mi dimentico). L'unimog (Mercedes) ha ponti (davanti e dietro) del tipo a U (di cui poi parleremo, dopo il ponte rigido; sempre che me ne ricordi).
cominciamo dalla sospensione a quadrilatero
però qui ho bisogno che qualcuno mi metta una bella foto di una sospensione a quadrilatero, che poi io riprenderò, modificherò e spiegherò.
chi mi aiuta?
p.s. potete mettere anche quella della 147, così è più bello
e preparate una foto di un McPherson
DENGHIU