Beccheggio.
Per quanto riguarda i movimenti attorno all’asse di beccheggio, prima di tutto bisognerà stabilire cosa (e quale) sia l’asse di beccheggio.
Per chiarirlo in modo evidente, guardate la figura qui sotto: nella vista dall’alto, l’asse di beccheggio è quello rappresentato dall’indice J (tralasciate il discorso tra sistema di riferimento delle masse sospese e sistema di riferimento delle masse non sospese).
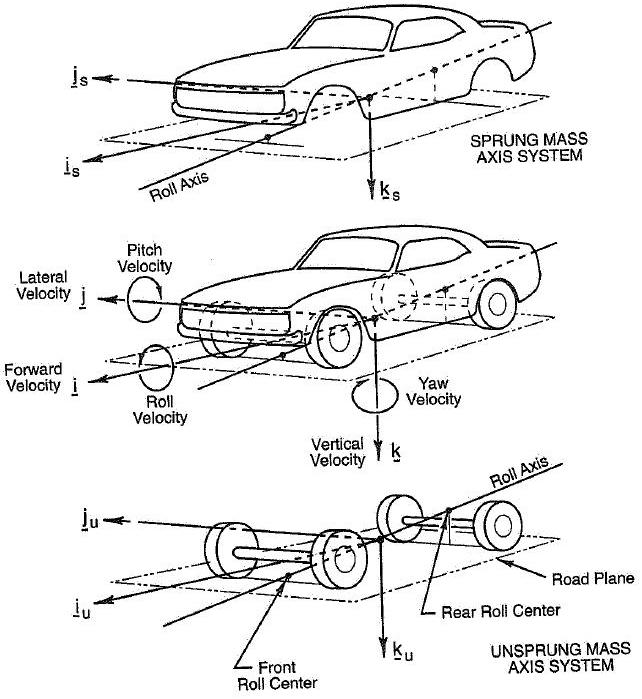
Tra i movimenti a beccheggio (le rotazioni attorno all’asse di beccheggio) e quelli a rollio ci sono molte analogie.
A cominciare dal concetto di trasferimento di carico. Abbiamo visto che, se percorro una curva, a causa della forza centrifuga F si genera un trasferimento di carico dalla ruota interna alla ruota esterna alla curva proporzionale alla forza F stessa, all’altezza di CG (punto di applicazione della forza F) e inversamente proporzionale alla larghezza della carreggiata dell’auto.
Nel caso in cui la forza F agisca, anziché in senso trasversale (come è la forza centrifuga), in senso longitudinale (come nel caso di una accelerazione o una frenata), invece del trasferimento di carico trasversale avrò un trasferimento di carico longitudinale. Più precisamente, nel caso in cui la macchina sia sottoposta ad una forza frenante (una frenata), avverrà un trasferimento di carico dall’asse posteriore (che si scarica) a quello anteriore; nel caso di accelerazione, il contrario. Il valore del trasferimento di carico W sarà sempre funzione proporzionale, come nel caso della forza centrifuga, dell’intensità di F (cioè della frenata o dell’accelerazione) e dell’altezza del CG; e inversamente proporzionale del….passo (al posto della carreggiata usata nel caso di forza trasversale).
Capite bene che le cose sono esattamente le stesse. Semplicemente, abbiamo trasferito i concetti dal trasversale al longitudinale.
Quindi, se guardate il disegno successivo che schematizza la macchina sottoposta ad una accelerazione longitudinale, e se indichiamo (come al solito) con CG il centro di gravità, con h la sua altezza dal suolo, con F la forza, e con l il passo (notate anche i valori a e b che indicano la distanza del CG dai due assi), possiamo scrivere (anche in questo caso) che il trasferimento di carico longitudinale W vale:
W = F h / l
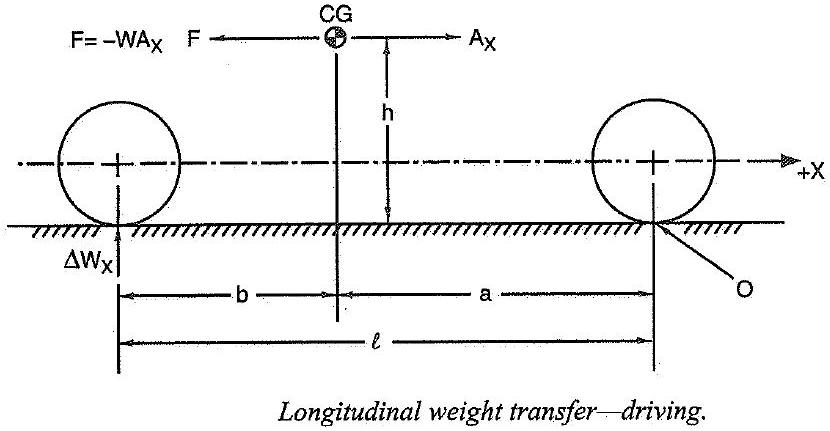
Vi prego anche di notare che nel disegno F viene indicata come – (meno) W Ax
Chiariamo subito:
1) Attenzione: non confondete il W che ho scritto io con il W indicato dal disegno e che va nella formula suddetta (F= -Wax). Con W io ho indicato il trasferimento di carico; nel disegno, con W si indica la massa dell’auto (anzi, per essere proprio preciso, l’autore di quel disegno ha indicato con W la FORZA peso dell’auto e con Ax l’accelerazione longitudinale espressa in g-force, cioè dividendola per l’accelerazione di gravità…ma lasciate perdere: supponete che W sia la massa e Ax l’accelerazione, e basta)
2) Il segno meno sta ad indicare che la forza F è una forza apparente (d’inerzia)!!! Anche noi lo abbiamo sempre detto e scritto, già fin da quando abbiamo parlato del rollio e del trasferimento di carico trasversale….tenetelo ben presente!!! Per esempio, se la mia macchina sta frenando, è sottoposta ad una forza (di frenata) che la spinge dal davanti al dietro, ma la forza (apparente) d’inerzia ha il verso in avanti. Insomma, questo dipende dalla teoria della relatività galileiana…Però voglio che sia ben chiaro.
Torniamo al trasferimento di carico.
Quindi, in caso di frenata, l’asse anteriore (adesso non ha più senso parlare di “sospensione” o di “ruota” anteriore o posteriore, a meno che non si consideri solo META’ macchina…) si caricherà di un ulteriore carico verticale mentre quello posteriore si scaricherà dello stesso valore; al contrario, in caso di accelerazione, sarà l’asse posteriore a caricarsi (di una forza verticale W = F h / l) e quello anteriore a scaricarsi.
Ora, è altrettanto chiaro che a causa di questi trasferimento di carico, le sospensioni anteriori e posteriori si abbasseranno e/o alzeranno in funzione del trasferimento di carico e della forza che riusciranno ad opporre a tale trasferimento di carico (la loro rigidezza). Ma anche (ed è la stessa cosa che abbiamo visto nel caso del rollio e dei trasferimenti di carico trasversali) della loro geometria. Questi cambiamenti nella geometria (compressioni ed estensioni) sono chiamati “dive”, “lift” e “squat”; e la capacità delle sospensioni di opporsi allo schiacciamento/estensione, coi termini “anti-dive” “anti-lift” e “anti-squat”.
Vi ricordate che, quando abbiamo parlato del rollio, abbiamo detto che una parte del momento di ribaltamento andava direttamente alle sospensioni e un’altra parte serviva per far rollare la cassa? Bene: qui è la stessa cosa.
Per chiarirla dobbiamo però fare ancora un passettino. Diciamo che, anche in senso longitudinale, esisterà un centro di istantanea rotazione della scocca rispetto alla strada (che passa per le sospensioni). Solo che qui non siamo come nel caso del rollio, con le sospensioni di destra e di sinistra simmetriche. In questo caso, le sospensioni anteriori potranno essere di un tipo, quelle posteriori di un altro tipo. Ma non fa niente, perché comunque, riusciremo a determinare un centro di istantanea rotazione. Come?
Semplice: guardate la figura qui sotto: rappresenta la vista di fianco di 2 tipologie differenti di sospensioni, un McPherson (sopra) e un quadrilatero (sotto). Il punto L.S.C. (Longitudinal swing center) è il centro di istantanea rotazione (longitudinale) della scocca rispetto alla sospensione.
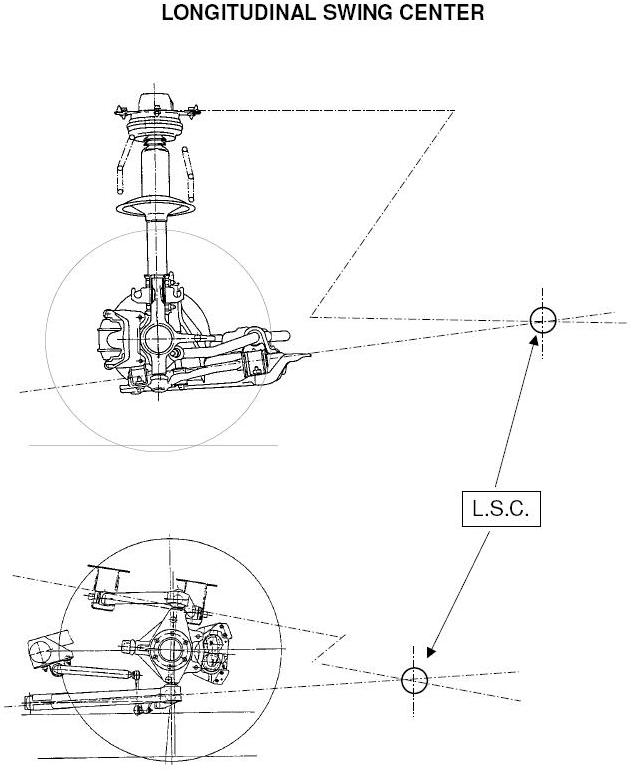
Adesso, manca la rotazione della sospensione al terreno, che è il punto di contatto della ruota al terreno. Quindi, tiro un altro segmento che passerà per quest’ultimo punto e per il mio L.S.C. Osservate il prossimo disegno.
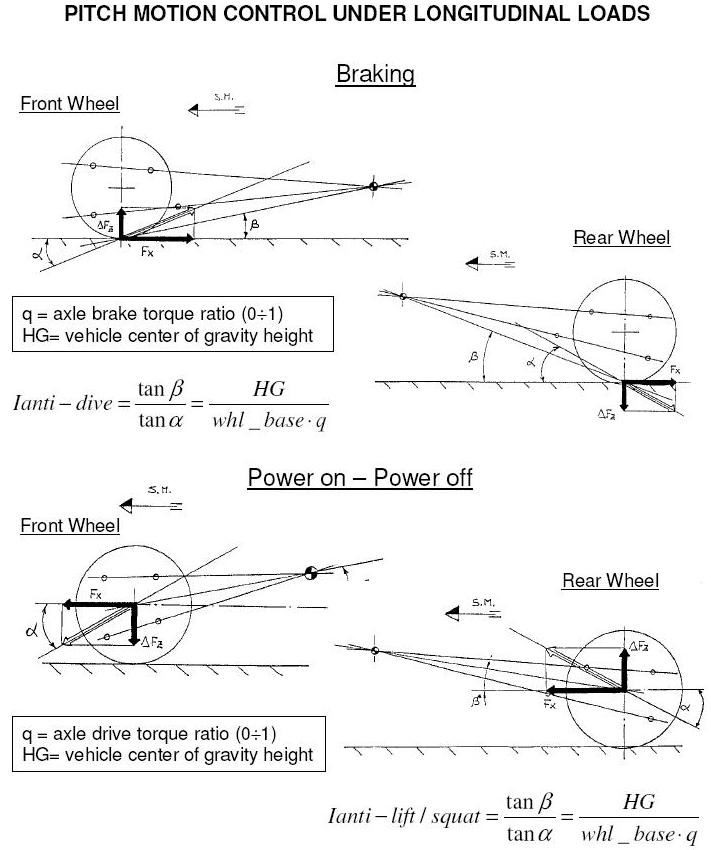
Vedete, nel primo disegno nel caso di frenata, che si creano due angoli: il primo (β) è l’angolo formato dalla retta che unisce l’L.S.C. con il punto a terra; l’altro (α), fatto da un segmento che passa sempre per il punto a terra del pneumatico e per…….per il CG (che lì non è disegnato). Bene: si definisce “percentuale di anti-XXX” (in questo caso specifico sarebbe “percentuale di anti-dive”) della sospensione il rapporto tra l’altezza sul terreno dell’L.S.C. e l’altezza h del CG.
Quindi, sempre riferendomi alla figura, avrò:
1) nel caso di frenata:
- per la sospensione anteriore una percentuale di “anti-dive”
- per la sospensione posteriore una percentuale di “anti-lift”
2) in caso di trazione (accelerazione):
- per la sospensione anteriore una percentuale di “anti-lift”
- per la sospensione posteriore una percentuale di “anti-squat”
Attenzione però: guardate sempre la figura e riferitevi al caso di accelerazione: in questo caso, poiché le forze di trazione vengono applicate A CENTRO RUOTA, la determinazione della percentuale di “anti-qualcosa” viene riferita al centro ruota.
Ora, è chiaro che, se consideriamo per esempio la sospensione anteriore, se il centro di istantanea rotazione della sospensione (L.S.C.) è alla stessa quota del CG, in caso di frenata avrò una percentuale di “anti-dive” del 100% (essendo il rapporto % = L.S.C. / h = 1). Lo stesso vale negli altri casi con l’accortezza di utilizzare la corretta terminologia e fare bene i conti.
Qui sotto vedete i due L.S.C. delle due sospensioni in relazione al CG:
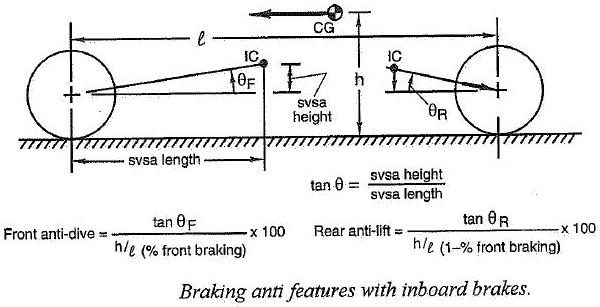
In funzione di come inclino trasversalmente i bracci della sospensione, otterrò una più o meno elevata "rigidezza" al dive al lift e allo squat.
Vi ripropongo qui di seguito la procedura grafica per determinare gli angoli di antidive ed antilift. Ricordo che l’angolo antidive misura la capacità della sospensione di limitare l’abbassamento del muso del veicolo in frenata; il muso non si abbassa, se la risultante delle forze frenanti applicata alla sospensione, passa per il centro di beccheggio. e le forze frananti, come noto, sono applicate nel punto di contatto ruota suolo. L’angolo di antilift e’ legato, invece, alla capacità di impedire il sollevamento del muso del veicolo in accelerazione; la diversità fra i due angoli è legata alla diversa modalità di applicazione dei momenti motori e frenanti.
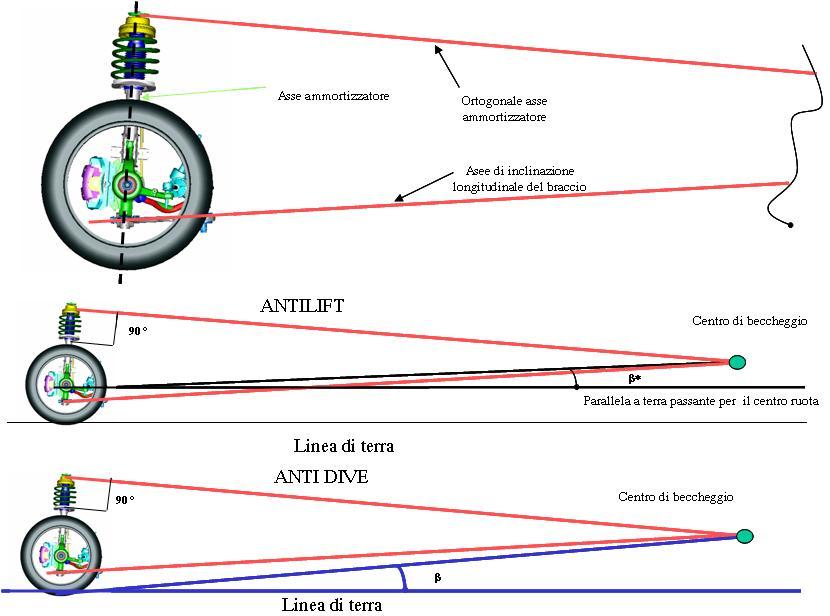
Stessa cosa qui. Guardate bene dove sta l'asse di beccheggio:
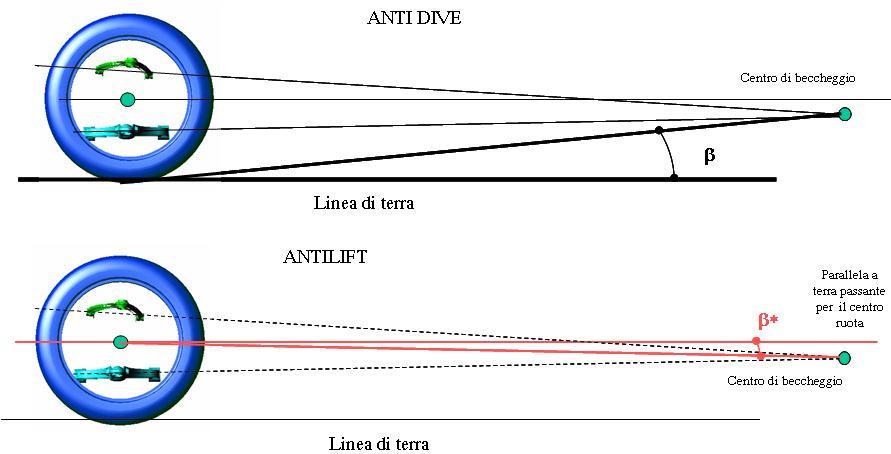
Vediamo di spiegarci meglio e con un paio di esempi.
Vi ricordate quando parlavamo del rollio, quando definimmo il CG e il CR e dicemmo che se CG non coincide con CR allora ho rollio; invece se CG e CR coincidono, allora non ho rollio; ma comunque, il trasferimento di carico c’è sempre, eccetera eccetera? Bene, qui è lo stesso.
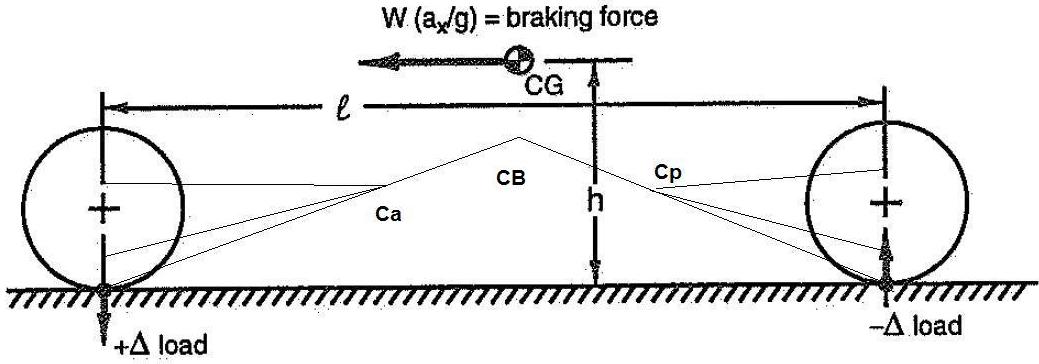
Caso 1: macchina in frenata. Forza F applicata come sempre al baricentro. Il mio trasferimento di carico vale, come sempre, W = F h / l (in figura è indicato con Δ load).
Dalla geometria delle sospensioni (non mi interessa che tipo di sospensioni ho, per il momento; ma solo la definizione dei centri di istantanea rotazione) determino i centri di istantanea rotazione della scocca rispetto alle singole sospensioni (anteriore e posteriore) esattamente come facevo nel caso del rollio (e li indico con Ca e Cp). Poi, tiro il prolungamento al punto a terra delle singole ruote che passa per i due punti Ca e Cp. Questo prolungamento si incontrerà in quello che è il centro di istantanea rotazione della scocca rispetto al terreno passando per le sospensioni, che poi altro non è se non il punto immagine dell’asse di beccheggio, cioè il centro di beccheggio CB. Esattamente come nel caso del rollio.
Come vedete, il CG e il CB non coincidono. Questo vuol dire che, se applico una forza F al baricentro la macchina ruoterà attorno a CB. Il momento che farà ruotare la macchina sarà pari al prodotto della forza F moltiplicato per la distanza tra CG e CB.
Il trasferimento di carico vale sempre W = F h / l.
Caso 2: macchina sempre in frenata. Questa volta, la geometria delle sospensioni della mia macchina è tale che i due centri di istantanea rotazione Ca e Cp cadono sulle rette che congiungono il baricentro CG con i punti a terra delle due ruote. O meglio: dopo aver determinato Ca e Cp, tiro il prolungamento al punto a terra delle singole ruote che passa per i due punti Ca e Cp. Questo prolungamento si incontrerà in quello che è il centro di istantanea rotazione della scocca rispetto al terreno passando per le sospensioni che, in questo caso, è alla stessa altezza di CG; anzi, coincide proprio.
In questo caso, se applico una forza F al baricentro la macchina non ruoterà attorno a nulla, perché non ho momento di beccheggio. In ogni caso, ho sempre TRASFERIMENTO DI CARICO, che vale sempre W = F h / l.
Questa sospensione è, oltretutto, 100% antidive e 100% antilift. Perché i centri di istantanea rotazione Ca e Cp cadono sulle rette che congiungono il baricentro CG con i punti a terra delle due ruote.
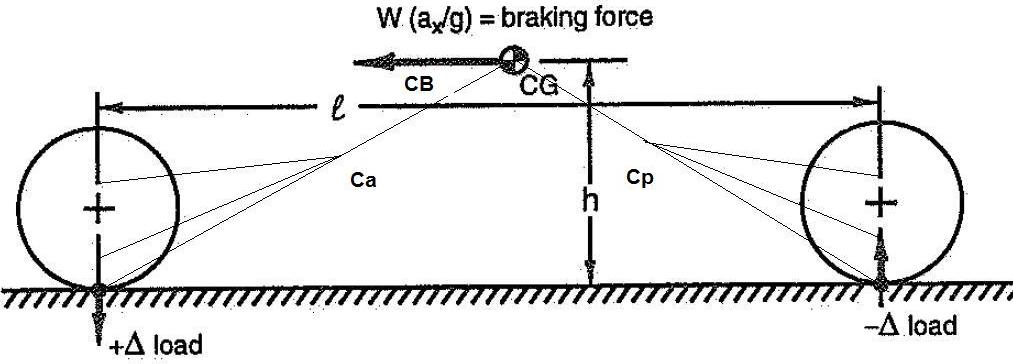
Torniamo al caso 1: in quel caso, invece, la mia percentuale di antidive sarà data, almeno graficamente, dal rapporto tra la distanza CG-CB e l’altezza h del baricentro CG (moltiplicato per 100). Idem per l’antilift posteriore.
Lo stesso procedimento si usa nel caso di accelerazione, tenendo presente quello che abbiamo detto ieri circa il punto di applicazione delle forze (in frenata al punto a terra, in accelerazione a centro ruota).
Quanto ai nomi: dive significa affondamento (dell’anteriore), lift significa sollevamento (sia davanti che dietro), squat significa affondamento (del posteriore).
Come nel caso del rollio, anche qui se alzo CB riduco il beccheggio ma aumento la parte di trasferimento di carico che passa direttamente ai pneumatici attraverso i bracci della sospensione. Se, viceversa, abbasso CB, il beccheggio della carrozzeria aumenta e deve essere contrastato dalle molle (irrigidendole).
Questa è, spero, una spiegazione semplice di un concetto piuttosto complicato.
Se dovessi spiegarvelo in modo analitico, dovrei tirare in ballo la ripartizione delle coppie frenanti (quindi delle forze alle ruote), cioè la ripartizione di frenata (ma di frenatura ne parleremo molto più avanti).
Domanda: cosa succede se ho una sospensione al 100% antidive? E perché non è conveniente?
Risposta: se ho 100% antidive, in pratica mi trovo con il centro di istantanea rotazione Ca della sospensione anteriore alla stessa altezza (o magari anche coincidente) con CG. Tutto il momento di beccheggio si trasferisce direttamente alle ruote passando per le sospensioni. Ma, in pratica, cosa succede?
Succede che la mia sospensione anteriore si comporta come se fosse infinitamente rigida, praticamente bloccata.
Ora, se pensate che la frenata è solo UNA delle condizioni in cui si genera una forza F (d'inerzia) con verso rivolto in avanti; e che di forze così ce ne possono essere altre, per esempio nel caso in cui dovessi affrontare una sconnessione stradale (un gradino, una traversina messa in senso trasversale), cosa succederebbe se avessi una macchina con sospensione anteriore 100% antidive? Succederebbe che, invece di filtrarla (con la deformazione della molla), la sospensione rimarrebbe totalmente rigida, indeformata. e l'accelerazione si trasmetterebbe TUTTA alla scocca e da qui ai passeggeri. In definitiva, la macchina "salterebbe" letteralmente sulla traversina, anziché assorbirla. Ecco perché si preferisce avere sospensioni anteriori (e anche posteriori) con poca percentuale antidive.
E poi, c'è un altro problema: avere un avantreno eccessivamente rigido, cosa comporta? Oltre al confort sugli ostacoli secchi, anche una maggiore sensibilità alle irregolarità del fondo in media/alta frequenza (quindi, sempre molto dis-confort); e poi, una rigidezza altissima davanti mi comporta una ripartizione di rigidezze tra anteriore e posteriore pessima, con tutte le conseguenze che ben sappiamo. Poi, come abbiamo visto tanto, tantissimo tempo fa, quando parlavamo dei bracci a terra (longitudinali, ma anche trasversali), cosa succede se, avendo un braccio a a terra trasversale di una certa entità, un certo valore di kingpin (sempre presente in certe sospensioni come il McPherson; quindi, praticamente su TUTTE le macchine che circolano attualmente per strada) e un certo, seppur minimo valore di camber, ho una sospensione 100% antidive? Che avrò anche una elevatissima difficoltà a girare il volante, ossia lo sterzo si irrigidisce tantissimo.
Fin qui abbiamo visto che per calcolare la percentuale di anti-dive dobbiamo misurare, in pratica, il rapporto tra 2 altezze, quella di Ca rispetto a quella di CG. altezze riferite al terreno. Tutto ciò nel caso di vettura dotata di freni normali, cioè pinze freni attaccate al mozzo (perché la percentuale di anti-dive rappresenta la percentuale di "resistenza", di qualcosa che si "oppone" all'affondamento della sospensione in caso di forza F d'inerzia con verso rivolto in avanti, come appunto in caso di frenata).
Ma se io ho in mano una vettura dotata di freni "entrobordo", cioè pinze freno fissate all'uscita del differenziale, prima dei semiassi? per esempio, se avessi in mano un'Alfasud?
Semplice, in questo caso, la coppia frenante può essere ritenuta equivalente ad una coppia motrice, ma di segno opposto. Quindi, riferisco tutto a centro ruota come, appunto, nel caso di trazione.
Quindi, facciamo due conti.
Supponiamo di avere due vetture esattamente uguali in tutto tranne che nei freni. una ha i freni sulla ruota (sui mozzi); l'altra, entrobordo.
Supponiamo che:
Ca sia posto a 60 cm da terra
CG sia posto ad 1 m.
Il raggio sotto carico della ruota (quindi il mio centro ruota) sia a circa 30 cm da terra.
Allora:
- la percentuale di anti-dive della vettura dotata di freni tradizionali sarà 60%;
- la percentuale di antidive della vettura con freni entrobordo sarà di circa 42-43%.
Ossia, si riduce. I freni entrobordo mi hanno fatto ridurre la capacità antidive della sospensione. Questo perché riferisco tutto al centro ruota.
Per i motivi suddetti, in genere sulle vetture stradali si preferisce avere basse percentuali di effetto antidive, mentre sulle vetture da corsa, l'effetto antidive è sicuramente più richiesto (ma sempre senza arrivare a valori estremi).
Anzi, sulle vetture di serie, si usano configurazioni di sospensioni in grado di generare un certo effetto pro-lift, che vada a favore dell'assorbimento delle sconnessioni.
Un certo effetto anti-lift della sospensione anteriore e anche anti-squat (della sospensione posteriore) è sicuramente positivo, perché riducono la cabrata in caso di accelerazione.
Anche in questo caso, comunque, si tende a non esagerare troppo con la posizione dei vari centri di istantanea rotazione. al limite, per evitare la cabrata, si lavora sulla rigidezza delle sospensioni posteriori!
All'opposto in caso di dive.
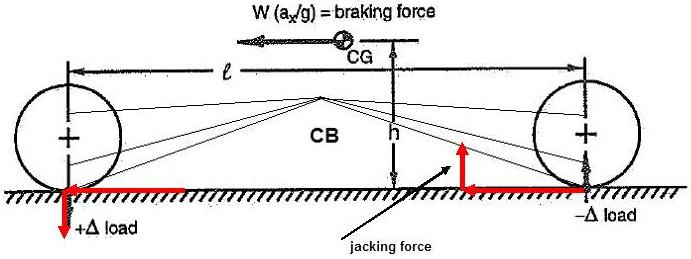
Come per il rollio, abbiamo la jacking force, dipendente dalla posizione del centro di beccheggio (CB): più è alto da terra, tanto maggiore sarà la jacking force.
Osservate lo schema seguente.
Le forze verticali in rosso sono i trasferimenti di carico (indicate anche con le frecce nere che non ho tolto, volutamente, e sono indicate con +/- Δ load).
Come vedete, se alzo CB la mia jacking force cresce. e anche se cresce la forza F.
Insomma, le cose vanno esattamente come nel caso del rollio.
Anzi, dirò di più: questi esempi che si riferiscono al caso del beccheggio vi possono servire anche per il rollio. Mi spiego meglio: nel rollio (a parte il fatto che la cassa rolla anziché beccheggiare) abbiamo definito CR con lo schema di sospensioni simmetriche a destra e a sinistra. Quindi, CR cade sull'asse di mezzeria della scocca perché i centri di istantanea rotazione dei singoli assi (che, nel caso di beccheggio, sono Ca e Cp) sono posti simmetricamente.
Nel caso di beccheggio, Ca e Cp possono essere (anzi, sicuramente sono) non simmetrici, magari uno più in alto dell'altro, perché le sospensioni anteriore e posteriore sono, praticamente sempre, estremamente diverse.
Ma in ultima analisi, i concetti sono sempre quelli.
Ora, un comportamento simile a questo descritto nel caso del beccheggio può essere rappresentativo nel caso di comportamento a rollio di una vettura con sospensioni di destra e di sinistra non simmetriche, per esempio nel caso di vetture da corsa per gare negli ovali (Nascar & co.): adesso sapete come funzionano queste vetture, che hanno un CR che non cade sull'asse di mezzeria della vettura e, per questo, si comportano differentemente a seconda che facciano una curva a destra o una a sinistra....
Quindi, sapete anche che, quando qualcuno (generalmente sarà un giornalista che si occupa di motori) dirà, come ho sentito io con le mie orecchie, che le vetture che corrono sugli ovali in America possono girare solo a sinistra dicono solo un sacco di cavolate (d'altronde, da un giornalista che prima lavorava nella redazione di "taglio e cucito" e poi è andato in una testata che parla di automobili, è il minimo che tu passa sentire...).
:grazie) alfistavero.
Per quanto riguarda i movimenti attorno all’asse di beccheggio, prima di tutto bisognerà stabilire cosa (e quale) sia l’asse di beccheggio.
Per chiarirlo in modo evidente, guardate la figura qui sotto: nella vista dall’alto, l’asse di beccheggio è quello rappresentato dall’indice J (tralasciate il discorso tra sistema di riferimento delle masse sospese e sistema di riferimento delle masse non sospese).

Tra i movimenti a beccheggio (le rotazioni attorno all’asse di beccheggio) e quelli a rollio ci sono molte analogie.
A cominciare dal concetto di trasferimento di carico. Abbiamo visto che, se percorro una curva, a causa della forza centrifuga F si genera un trasferimento di carico dalla ruota interna alla ruota esterna alla curva proporzionale alla forza F stessa, all’altezza di CG (punto di applicazione della forza F) e inversamente proporzionale alla larghezza della carreggiata dell’auto.
Nel caso in cui la forza F agisca, anziché in senso trasversale (come è la forza centrifuga), in senso longitudinale (come nel caso di una accelerazione o una frenata), invece del trasferimento di carico trasversale avrò un trasferimento di carico longitudinale. Più precisamente, nel caso in cui la macchina sia sottoposta ad una forza frenante (una frenata), avverrà un trasferimento di carico dall’asse posteriore (che si scarica) a quello anteriore; nel caso di accelerazione, il contrario. Il valore del trasferimento di carico W sarà sempre funzione proporzionale, come nel caso della forza centrifuga, dell’intensità di F (cioè della frenata o dell’accelerazione) e dell’altezza del CG; e inversamente proporzionale del….passo (al posto della carreggiata usata nel caso di forza trasversale).
Capite bene che le cose sono esattamente le stesse. Semplicemente, abbiamo trasferito i concetti dal trasversale al longitudinale.
Quindi, se guardate il disegno successivo che schematizza la macchina sottoposta ad una accelerazione longitudinale, e se indichiamo (come al solito) con CG il centro di gravità, con h la sua altezza dal suolo, con F la forza, e con l il passo (notate anche i valori a e b che indicano la distanza del CG dai due assi), possiamo scrivere (anche in questo caso) che il trasferimento di carico longitudinale W vale:
W = F h / l

Vi prego anche di notare che nel disegno F viene indicata come – (meno) W Ax
Chiariamo subito:
1) Attenzione: non confondete il W che ho scritto io con il W indicato dal disegno e che va nella formula suddetta (F= -Wax). Con W io ho indicato il trasferimento di carico; nel disegno, con W si indica la massa dell’auto (anzi, per essere proprio preciso, l’autore di quel disegno ha indicato con W la FORZA peso dell’auto e con Ax l’accelerazione longitudinale espressa in g-force, cioè dividendola per l’accelerazione di gravità…ma lasciate perdere: supponete che W sia la massa e Ax l’accelerazione, e basta)
2) Il segno meno sta ad indicare che la forza F è una forza apparente (d’inerzia)!!! Anche noi lo abbiamo sempre detto e scritto, già fin da quando abbiamo parlato del rollio e del trasferimento di carico trasversale….tenetelo ben presente!!! Per esempio, se la mia macchina sta frenando, è sottoposta ad una forza (di frenata) che la spinge dal davanti al dietro, ma la forza (apparente) d’inerzia ha il verso in avanti. Insomma, questo dipende dalla teoria della relatività galileiana…Però voglio che sia ben chiaro.
Torniamo al trasferimento di carico.
Quindi, in caso di frenata, l’asse anteriore (adesso non ha più senso parlare di “sospensione” o di “ruota” anteriore o posteriore, a meno che non si consideri solo META’ macchina…) si caricherà di un ulteriore carico verticale mentre quello posteriore si scaricherà dello stesso valore; al contrario, in caso di accelerazione, sarà l’asse posteriore a caricarsi (di una forza verticale W = F h / l) e quello anteriore a scaricarsi.
Ora, è altrettanto chiaro che a causa di questi trasferimento di carico, le sospensioni anteriori e posteriori si abbasseranno e/o alzeranno in funzione del trasferimento di carico e della forza che riusciranno ad opporre a tale trasferimento di carico (la loro rigidezza). Ma anche (ed è la stessa cosa che abbiamo visto nel caso del rollio e dei trasferimenti di carico trasversali) della loro geometria. Questi cambiamenti nella geometria (compressioni ed estensioni) sono chiamati “dive”, “lift” e “squat”; e la capacità delle sospensioni di opporsi allo schiacciamento/estensione, coi termini “anti-dive” “anti-lift” e “anti-squat”.
Vi ricordate che, quando abbiamo parlato del rollio, abbiamo detto che una parte del momento di ribaltamento andava direttamente alle sospensioni e un’altra parte serviva per far rollare la cassa? Bene: qui è la stessa cosa.
Per chiarirla dobbiamo però fare ancora un passettino. Diciamo che, anche in senso longitudinale, esisterà un centro di istantanea rotazione della scocca rispetto alla strada (che passa per le sospensioni). Solo che qui non siamo come nel caso del rollio, con le sospensioni di destra e di sinistra simmetriche. In questo caso, le sospensioni anteriori potranno essere di un tipo, quelle posteriori di un altro tipo. Ma non fa niente, perché comunque, riusciremo a determinare un centro di istantanea rotazione. Come?
Semplice: guardate la figura qui sotto: rappresenta la vista di fianco di 2 tipologie differenti di sospensioni, un McPherson (sopra) e un quadrilatero (sotto). Il punto L.S.C. (Longitudinal swing center) è il centro di istantanea rotazione (longitudinale) della scocca rispetto alla sospensione.

Adesso, manca la rotazione della sospensione al terreno, che è il punto di contatto della ruota al terreno. Quindi, tiro un altro segmento che passerà per quest’ultimo punto e per il mio L.S.C. Osservate il prossimo disegno.

Vedete, nel primo disegno nel caso di frenata, che si creano due angoli: il primo (β) è l’angolo formato dalla retta che unisce l’L.S.C. con il punto a terra; l’altro (α), fatto da un segmento che passa sempre per il punto a terra del pneumatico e per…….per il CG (che lì non è disegnato). Bene: si definisce “percentuale di anti-XXX” (in questo caso specifico sarebbe “percentuale di anti-dive”) della sospensione il rapporto tra l’altezza sul terreno dell’L.S.C. e l’altezza h del CG.
Quindi, sempre riferendomi alla figura, avrò:
1) nel caso di frenata:
- per la sospensione anteriore una percentuale di “anti-dive”
- per la sospensione posteriore una percentuale di “anti-lift”
2) in caso di trazione (accelerazione):
- per la sospensione anteriore una percentuale di “anti-lift”
- per la sospensione posteriore una percentuale di “anti-squat”
Attenzione però: guardate sempre la figura e riferitevi al caso di accelerazione: in questo caso, poiché le forze di trazione vengono applicate A CENTRO RUOTA, la determinazione della percentuale di “anti-qualcosa” viene riferita al centro ruota.
Ora, è chiaro che, se consideriamo per esempio la sospensione anteriore, se il centro di istantanea rotazione della sospensione (L.S.C.) è alla stessa quota del CG, in caso di frenata avrò una percentuale di “anti-dive” del 100% (essendo il rapporto % = L.S.C. / h = 1). Lo stesso vale negli altri casi con l’accortezza di utilizzare la corretta terminologia e fare bene i conti.
Qui sotto vedete i due L.S.C. delle due sospensioni in relazione al CG:

In funzione di come inclino trasversalmente i bracci della sospensione, otterrò una più o meno elevata "rigidezza" al dive al lift e allo squat.
Vi ripropongo qui di seguito la procedura grafica per determinare gli angoli di antidive ed antilift. Ricordo che l’angolo antidive misura la capacità della sospensione di limitare l’abbassamento del muso del veicolo in frenata; il muso non si abbassa, se la risultante delle forze frenanti applicata alla sospensione, passa per il centro di beccheggio. e le forze frananti, come noto, sono applicate nel punto di contatto ruota suolo. L’angolo di antilift e’ legato, invece, alla capacità di impedire il sollevamento del muso del veicolo in accelerazione; la diversità fra i due angoli è legata alla diversa modalità di applicazione dei momenti motori e frenanti.

Stessa cosa qui. Guardate bene dove sta l'asse di beccheggio:

Vediamo di spiegarci meglio e con un paio di esempi.
Vi ricordate quando parlavamo del rollio, quando definimmo il CG e il CR e dicemmo che se CG non coincide con CR allora ho rollio; invece se CG e CR coincidono, allora non ho rollio; ma comunque, il trasferimento di carico c’è sempre, eccetera eccetera? Bene, qui è lo stesso.
Caso 1: macchina in frenata. Forza F applicata come sempre al baricentro. Il mio trasferimento di carico vale, come sempre, W = F h / l (in figura è indicato con Δ load).
Dalla geometria delle sospensioni (non mi interessa che tipo di sospensioni ho, per il momento; ma solo la definizione dei centri di istantanea rotazione) determino i centri di istantanea rotazione della scocca rispetto alle singole sospensioni (anteriore e posteriore) esattamente come facevo nel caso del rollio (e li indico con Ca e Cp). Poi, tiro il prolungamento al punto a terra delle singole ruote che passa per i due punti Ca e Cp. Questo prolungamento si incontrerà in quello che è il centro di istantanea rotazione della scocca rispetto al terreno passando per le sospensioni, che poi altro non è se non il punto immagine dell’asse di beccheggio, cioè il centro di beccheggio CB. Esattamente come nel caso del rollio.
Come vedete, il CG e il CB non coincidono. Questo vuol dire che, se applico una forza F al baricentro la macchina ruoterà attorno a CB. Il momento che farà ruotare la macchina sarà pari al prodotto della forza F moltiplicato per la distanza tra CG e CB.
Il trasferimento di carico vale sempre W = F h / l.

Caso 2: macchina sempre in frenata. Questa volta, la geometria delle sospensioni della mia macchina è tale che i due centri di istantanea rotazione Ca e Cp cadono sulle rette che congiungono il baricentro CG con i punti a terra delle due ruote. O meglio: dopo aver determinato Ca e Cp, tiro il prolungamento al punto a terra delle singole ruote che passa per i due punti Ca e Cp. Questo prolungamento si incontrerà in quello che è il centro di istantanea rotazione della scocca rispetto al terreno passando per le sospensioni che, in questo caso, è alla stessa altezza di CG; anzi, coincide proprio.
In questo caso, se applico una forza F al baricentro la macchina non ruoterà attorno a nulla, perché non ho momento di beccheggio. In ogni caso, ho sempre TRASFERIMENTO DI CARICO, che vale sempre W = F h / l.
Questa sospensione è, oltretutto, 100% antidive e 100% antilift. Perché i centri di istantanea rotazione Ca e Cp cadono sulle rette che congiungono il baricentro CG con i punti a terra delle due ruote.

Torniamo al caso 1: in quel caso, invece, la mia percentuale di antidive sarà data, almeno graficamente, dal rapporto tra la distanza CG-CB e l’altezza h del baricentro CG (moltiplicato per 100). Idem per l’antilift posteriore.
Lo stesso procedimento si usa nel caso di accelerazione, tenendo presente quello che abbiamo detto ieri circa il punto di applicazione delle forze (in frenata al punto a terra, in accelerazione a centro ruota).
Quanto ai nomi: dive significa affondamento (dell’anteriore), lift significa sollevamento (sia davanti che dietro), squat significa affondamento (del posteriore).
Come nel caso del rollio, anche qui se alzo CB riduco il beccheggio ma aumento la parte di trasferimento di carico che passa direttamente ai pneumatici attraverso i bracci della sospensione. Se, viceversa, abbasso CB, il beccheggio della carrozzeria aumenta e deve essere contrastato dalle molle (irrigidendole).
Questa è, spero, una spiegazione semplice di un concetto piuttosto complicato.
Se dovessi spiegarvelo in modo analitico, dovrei tirare in ballo la ripartizione delle coppie frenanti (quindi delle forze alle ruote), cioè la ripartizione di frenata (ma di frenatura ne parleremo molto più avanti).
Domanda: cosa succede se ho una sospensione al 100% antidive? E perché non è conveniente?
Risposta: se ho 100% antidive, in pratica mi trovo con il centro di istantanea rotazione Ca della sospensione anteriore alla stessa altezza (o magari anche coincidente) con CG. Tutto il momento di beccheggio si trasferisce direttamente alle ruote passando per le sospensioni. Ma, in pratica, cosa succede?
Succede che la mia sospensione anteriore si comporta come se fosse infinitamente rigida, praticamente bloccata.
Ora, se pensate che la frenata è solo UNA delle condizioni in cui si genera una forza F (d'inerzia) con verso rivolto in avanti; e che di forze così ce ne possono essere altre, per esempio nel caso in cui dovessi affrontare una sconnessione stradale (un gradino, una traversina messa in senso trasversale), cosa succederebbe se avessi una macchina con sospensione anteriore 100% antidive? Succederebbe che, invece di filtrarla (con la deformazione della molla), la sospensione rimarrebbe totalmente rigida, indeformata. e l'accelerazione si trasmetterebbe TUTTA alla scocca e da qui ai passeggeri. In definitiva, la macchina "salterebbe" letteralmente sulla traversina, anziché assorbirla. Ecco perché si preferisce avere sospensioni anteriori (e anche posteriori) con poca percentuale antidive.
E poi, c'è un altro problema: avere un avantreno eccessivamente rigido, cosa comporta? Oltre al confort sugli ostacoli secchi, anche una maggiore sensibilità alle irregolarità del fondo in media/alta frequenza (quindi, sempre molto dis-confort); e poi, una rigidezza altissima davanti mi comporta una ripartizione di rigidezze tra anteriore e posteriore pessima, con tutte le conseguenze che ben sappiamo. Poi, come abbiamo visto tanto, tantissimo tempo fa, quando parlavamo dei bracci a terra (longitudinali, ma anche trasversali), cosa succede se, avendo un braccio a a terra trasversale di una certa entità, un certo valore di kingpin (sempre presente in certe sospensioni come il McPherson; quindi, praticamente su TUTTE le macchine che circolano attualmente per strada) e un certo, seppur minimo valore di camber, ho una sospensione 100% antidive? Che avrò anche una elevatissima difficoltà a girare il volante, ossia lo sterzo si irrigidisce tantissimo.
Fin qui abbiamo visto che per calcolare la percentuale di anti-dive dobbiamo misurare, in pratica, il rapporto tra 2 altezze, quella di Ca rispetto a quella di CG. altezze riferite al terreno. Tutto ciò nel caso di vettura dotata di freni normali, cioè pinze freni attaccate al mozzo (perché la percentuale di anti-dive rappresenta la percentuale di "resistenza", di qualcosa che si "oppone" all'affondamento della sospensione in caso di forza F d'inerzia con verso rivolto in avanti, come appunto in caso di frenata).
Ma se io ho in mano una vettura dotata di freni "entrobordo", cioè pinze freno fissate all'uscita del differenziale, prima dei semiassi? per esempio, se avessi in mano un'Alfasud?
Semplice, in questo caso, la coppia frenante può essere ritenuta equivalente ad una coppia motrice, ma di segno opposto. Quindi, riferisco tutto a centro ruota come, appunto, nel caso di trazione.
Quindi, facciamo due conti.
Supponiamo di avere due vetture esattamente uguali in tutto tranne che nei freni. una ha i freni sulla ruota (sui mozzi); l'altra, entrobordo.
Supponiamo che:
Ca sia posto a 60 cm da terra
CG sia posto ad 1 m.
Il raggio sotto carico della ruota (quindi il mio centro ruota) sia a circa 30 cm da terra.
Allora:
- la percentuale di anti-dive della vettura dotata di freni tradizionali sarà 60%;
- la percentuale di antidive della vettura con freni entrobordo sarà di circa 42-43%.
Ossia, si riduce. I freni entrobordo mi hanno fatto ridurre la capacità antidive della sospensione. Questo perché riferisco tutto al centro ruota.
Per i motivi suddetti, in genere sulle vetture stradali si preferisce avere basse percentuali di effetto antidive, mentre sulle vetture da corsa, l'effetto antidive è sicuramente più richiesto (ma sempre senza arrivare a valori estremi).
Anzi, sulle vetture di serie, si usano configurazioni di sospensioni in grado di generare un certo effetto pro-lift, che vada a favore dell'assorbimento delle sconnessioni.
Un certo effetto anti-lift della sospensione anteriore e anche anti-squat (della sospensione posteriore) è sicuramente positivo, perché riducono la cabrata in caso di accelerazione.
Anche in questo caso, comunque, si tende a non esagerare troppo con la posizione dei vari centri di istantanea rotazione. al limite, per evitare la cabrata, si lavora sulla rigidezza delle sospensioni posteriori!
All'opposto in caso di dive.
Come per il rollio, abbiamo la jacking force, dipendente dalla posizione del centro di beccheggio (CB): più è alto da terra, tanto maggiore sarà la jacking force.
Osservate lo schema seguente.
Le forze verticali in rosso sono i trasferimenti di carico (indicate anche con le frecce nere che non ho tolto, volutamente, e sono indicate con +/- Δ load).
Come vedete, se alzo CB la mia jacking force cresce. e anche se cresce la forza F.
Insomma, le cose vanno esattamente come nel caso del rollio.
Anzi, dirò di più: questi esempi che si riferiscono al caso del beccheggio vi possono servire anche per il rollio. Mi spiego meglio: nel rollio (a parte il fatto che la cassa rolla anziché beccheggiare) abbiamo definito CR con lo schema di sospensioni simmetriche a destra e a sinistra. Quindi, CR cade sull'asse di mezzeria della scocca perché i centri di istantanea rotazione dei singoli assi (che, nel caso di beccheggio, sono Ca e Cp) sono posti simmetricamente.
Nel caso di beccheggio, Ca e Cp possono essere (anzi, sicuramente sono) non simmetrici, magari uno più in alto dell'altro, perché le sospensioni anteriore e posteriore sono, praticamente sempre, estremamente diverse.
Ma in ultima analisi, i concetti sono sempre quelli.
Ora, un comportamento simile a questo descritto nel caso del beccheggio può essere rappresentativo nel caso di comportamento a rollio di una vettura con sospensioni di destra e di sinistra non simmetriche, per esempio nel caso di vetture da corsa per gare negli ovali (Nascar & co.): adesso sapete come funzionano queste vetture, che hanno un CR che non cade sull'asse di mezzeria della vettura e, per questo, si comportano differentemente a seconda che facciano una curva a destra o una a sinistra....
Quindi, sapete anche che, quando qualcuno (generalmente sarà un giornalista che si occupa di motori) dirà, come ho sentito io con le mie orecchie, che le vetture che corrono sugli ovali in America possono girare solo a sinistra dicono solo un sacco di cavolate (d'altronde, da un giornalista che prima lavorava nella redazione di "taglio e cucito" e poi è andato in una testata che parla di automobili, è il minimo che tu passa sentire...).

:grazie) alfistavero.

