PNEUMATICI
Tratteremo qui di seguito l’argomento del pneumatico, cos’è, a cosa deve soddisfare, quali sono le sue caratteristiche.
Ma prima, introduco due considerazioni iniziali.
La prima, faceva parte di una delle domande chiave che l'ing. Forghieri (sapete chi è?) poneva ai neolaureati per vedere se era il caso di assumerli (sia in ferrari sia in Oral) o no.
Le ruote sono quei componenti attraverso cui la macchina è collegata al terreno. con cui, insomma, scambia forze per andare, fermarsi, curvare, accelerare, etc.
Perché ciò avvenga, LE RUOTE DEVONO GIRARE, DEVONO ROTOLARE!!!! se la ruota striscia (sgomma o scivola di lato) NON TRASMETTE ALCUNA FORZA!!!!
Questo deve essere ben chiaro.
Forghieri faceva una domanda di questo tipo: metteva una macchinina con le ruote posteriori bloccate (un modellino di F1) su un piano inclinato, la faceva scendere e questa, naturalmente, cadeva dal piano inclinato. allora chiedeva: "Perché succede questo?"
La risposta era: perché il posteriore non fa più tenuta....
Sembra una stupidaggine, ma vi posso assicurare che ne faceva fuori tante, di giovani promesse!
La seconda: la ruota trasmette (scambia) le forze tra terreno e veicolo. Bene. TUTTE le forze, diciamo così, "dissipative" (frenata, aderenza trasversale, resistenza all'avanzamento, le forze dovute agli ostacoli incontrati sulla strada, etc) sono applicate nella zona di contatto col terreno (A TERRA); TUTTE le forze motrici (conseguenza delle coppie motrici) sono applicate A CENTRO RUOTA.
Per cui, quando dovremo ragionare sugli effetti di una forza frenante, dovremo fare riferimento ai bracci a terra; quando parleremo di forze di trazione, dovremo considerare i bracci a centro ruota.
Tanto per chiarire meglio, guardiamo il disegno seguente.
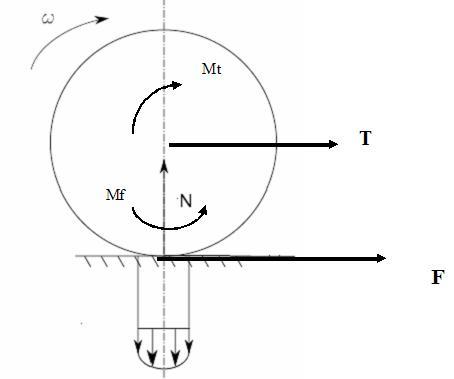
Abbiamo:
- la forza N, che è NORMALE (cioè perpendicolare) al piano stradale. essa rappresenta la reazione vincolare della strada alla forza normale che agisce sulla ruota (nel nostro caso, visto che siamo in piano, questa è rappresentata dal peso che grava sulla ruota, oltre al peso della ruota stessa)
- la forza T, applicata al centro della ruota: è la forza di trazione conseguente alla coppia motrice data dal motore e applicata ai semiassi a centro ruota (la quale coppia, se la divido per il raggio della ruota mi dà la forza di trazione)
- la forza F frenante: è conseguenza del momento frenante generato dalle pinze freno. anche in questo caso, se divido il momento per il raggio della ruota ho la forza frenante.
- Infine, ho aggiunto anche i momenti (Mt è la coppia motrice; Mf è il momento frenante...). come vedete, i momenti ci sono, eccome. però i punti di applicazione delle forze di trazione e di frenatura sono differenti: la forza di trazione è applicata a centro ruota; la forza frenante al centro dell'orma di contatto.
Definizione di Centro della ruota e Asse di istantanea rotazione della ruota.
Osservate bene la figura sottostante.
Il punto O si chiama “centro della ruota” o anche “asse della ruota” (se pensiamo che quella disegnata è solo la vista laterale…).
La ruota è supposta in movimento, con una certa velocità parallela alla strada (la V rossa) applicata al suo asse di rotazione. La ruota dunque TRASLA con velocità V costante. Quindi si dice che l’asse della ruota ha un moto traslatorio uniforme.
Però, la ruota, oltre a traslare, ha anche un moto rotatorio attorno al proprio asse O e dunque ruota con velocità angolare ω, che dipende dalla velocità V e dal raggio della ruota stessa (ma anche da altri parametri che per adesso non introduciamo).
Insomma, a me interessa che sappiate cosa sia l’asse ruota e il centro ruota (che sono poi lo stesso punto, in un disegno); ma anche che cosa sia CENTRO (O ASSE) DI ISTANTANEA ROTAZIONE della ruota.
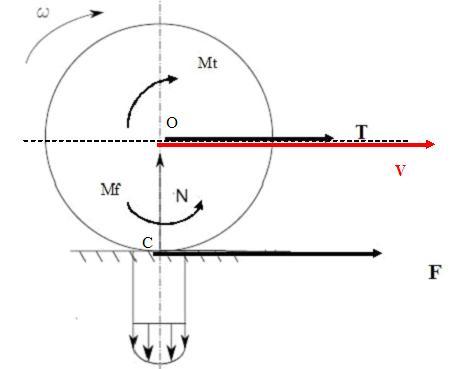
Se conosco V, in ogni istante, in realtà, la ruota “rotola” appunto attorno ad un punto (che è quello indicato con C) che è il punto di contatto della ruota con la strada. Insomma, in termini fisici si dice che in ogni istante si può definire un punto (o un asse) centro dell’atto di moto della ruota.
In parole più semplici, è solo il punto (o l’asse) attorno a cui la ruota rotola istante per istante…quindi il centro ruota O RUOTA anche lui attorno a questo punto, che rimane immobile: infatti, come vedete dal disegno, il punto O (centro ruota) ha una velocità (che è la velocità del centro ruota, la velocità di traslazione, quella indicata con la V rossa). Il punto C NON ha alcuna velocità: è fermo!
Quindi, riassumendo, abbiamo definito il centro ruota e il centro di istantanea rotazione (dell’atto di moto) della ruota: nel disegno, rispettivamente O e C.
Abbiamo visto il punto C, centro di istantanea rotazione della ruota. Bene: C è anche il punto di contatto tra la ruota e la strada. Osservate la figura qui sotto.
Guardate il caso ideale (a).
Nel punto di contatto tra la ruota e la strada viene applicata la forza N che è la reazione vincolare della strada alla forza NORMALE (cioè perpendicolare) applicata alla ruota. Nel nostro caso, visto che siamo in piano, questa forza normale altro non è se non la forza peso della ruota (il carico applicato alla ruota). Questa forza peso altro non sarà se non il peso della ruota + la parte del peso dell’auto che compete alla ruota. Se ho solo la ruota e basta, sarà solo il peso della ruota.
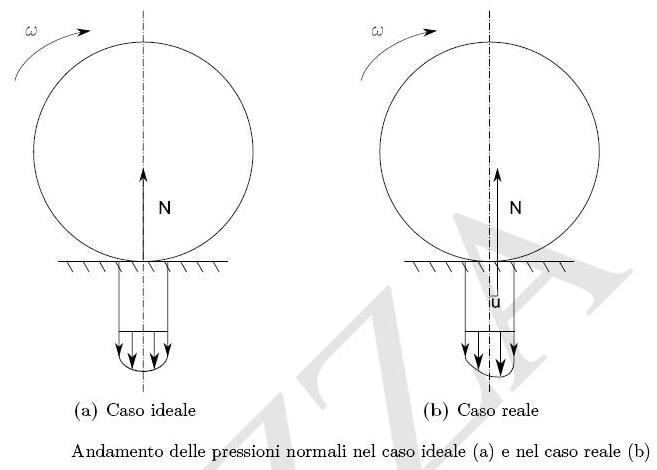
Bene: nel caso ideale, il contatto tra ruota e strada è puntiforme (il punto C).
Peccato, però, che nella REALTA’ le cose vadano diversamente.
In realtà, infatti, si tiene conto della deformabilità della ruota (cioè cerchio + pneumatico) e si ammette che il contatto del pneumatico con la strada non avvenga solo in un punto (il punto C), ma su una superficie limitata chiamata “orma di contatto” (o “superficie di contatto”). Questa superficie ha una sua propria grandezza, definita come “area dell’orma di contatto” (o “area della superficie di contatto”; o anche “area dell’impronta”).
A questo punto, ci aggiungiamo anche che il pneumatico NON è perfettamente elastico: quando io deformo il pneumatico per farlo rotolare, gli do una certa energia che, dopo la deformazione, quando il pneumatico tende a riprendere la propria forma, non viene interamente restituita. Parte di questa energia, viene persa a causa delle dissipazioni (delle perdite) all’interno del materiale.
Queste perdite sono dovute all’ISTERESI del materiale con cui sono fatti i pneumatici. Di conseguenza, si è visto sperimentalmente che per rotolare il pneumatico richiede di spendere una certa energia. Questo equivale ad una distribuzione delle pressioni la cui risultante è leggermente spostata in avanti nel senso del moto: guardate il disegno del caso reale (b) e confrontatelo con il caso ideale (a).
Come vedete, la forza N, che rappresenta la reazione vincolare della forza normale al terreno (nonché la risultante della distribuzione delle pressioni) è spostata in avanti rispetto al centro di istantanea rotazione. E guardate anche la distribuzione delle pressioni: nel caso ideale, tale distribuzione è simmetrica; nel caso reale, è asimmetrica con il picco verso l’avanti.
Questo rappresenta la spiegazione tecnica dell’isteresi del pneumatico. In pratica, anche senza applicare forze resistenti, la ruota, per rotolare, dissipa energia!
Naturalmente, l’energia persa è funzione della deformazione del pneumatico; quindi, delle caratteristiche costruttive del pneumatico stesso (tipo di materiale, tipo di pneumatico cioè se radiale o a tele incrociate; dimensioni del pneumatico, larghezza del battistrada, etc) e di caratteristiche esterne (pressione di gonfiaggio, carico verticale sul pneumatico, etc). Per esempio, i pneumatici “verdi” sono pneumatici realizzati con materiali “a bassa isteresi”, che si deformano poco; ma, per questo, “tengono” anche meno…
Chiaramente, tanto maggiore sarà l’isteresi del pneumatico, tanto maggiore sarà l’energia persa per il rotolamento, tanto maggiore l’energia necessaria per far rotolare il pneumatico…ciò equivale a “spostare” sempre più in avanti il punto di applicazione della forza N…
La coppia resistente (il momento resistente), rispetto al centro di rotazione O, sarà il prodotto della forza N moltiplicata per il braccio (la distanza del punto di applicazione di N) dal punto di contatto C: nel disegno, Mf = N u
Condizione di puro rotolamento.
Definiamo la condizione di puro rotolamento.
A livello intuitivo, possiamo capirla benissimo: la ruota rotola e basta.
A livello scientifico, diciamo che la condizione di PURO ROTOLAMENTO è quella in cui non sono applicate coppie all'asse della ruota (quello che abbiamo indicato nella figura precedente con O).
In questa condizione, il mozzo (cioè il centro O) si muove con velocità V diretta parallelamente alla strada.
Raggio di rotolamento.
Osservate la figura seguente.
Consideriamo una ruota di raggio R in rotolamento puro, cioè senza che su di essa agisca alcuna coppia motrice o frenante. Il centro della ruota si muove a velocità V e la ruota rotola con velocità angolare ω.
Il raggio di rotolamento è definito come il rapporto tra V e ω. Ossia, R0 = V/ ω.
Per farla breve, e semplice, si può dimostrare che Ro è compreso tra un valore minimo ed uno massimo. Il valore massimo è il valore del raggio della ruota scarica (cioè R); quello minimo, è l’altezza del centro della ruota sul suolo h (che prende il nome di raggio sotto carico).
Insomma, se scrivo quello che ho detto in termini matematici, avrò che h<R0<R.
Quello che m’interessa che comprendiate è che la velocità periferica di ogni punto del battistrada VARIA CICLICAMENTE. Cioè, un qualunque punto del battistrada, se non è a contatto col suolo, dapprima, avrà all’inizio una velocità periferica pari a ωR. Quando però arriva a contatto col suolo, la sua velocità (periferica) rallenta e, partendo da ωR si avvicina sempre più a ωh.
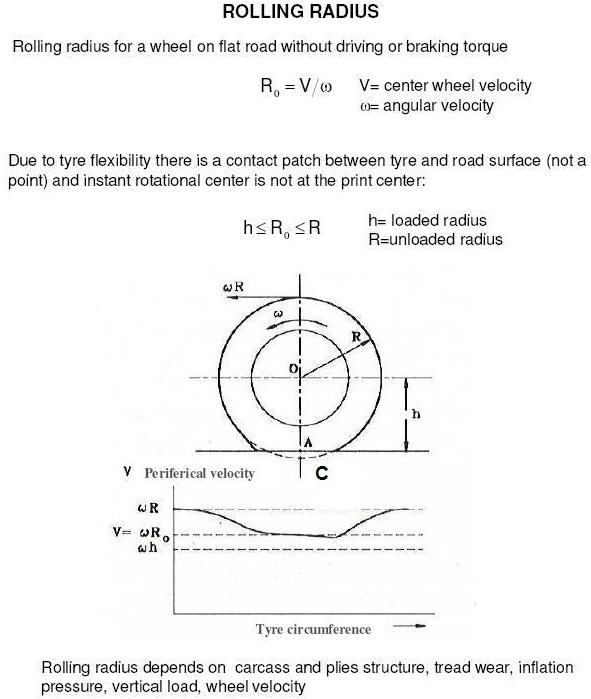
Questo significa che in questa prima fase, cioè dalla condizione indeformata fino ad A, il punto del battistrada STRISCIA e rallenta. Quando arriva in A, però, la velocità non diventa ωh, ma rimane sempre superiore, cioè anche in A continua a strisciare (di poco, ma striscia).
Da A in poi, invece, il punto riaccelera per raggiungere nuovamente la velocità ωR della ruota indeformata. Ovvero, dopo aver lasciato l’orma di contatto assume nuovamente la sua lunghezza iniziale e ritorna la valore iniziale ωR.
Se guardate il grafico che c’è allegato nel disegno, vedete come varia la velocità del singolo punto del battistrada con il rotolamento.
Questo significa che, nel primo tratto (cioè nella fase in cui rallenta passando da ωR per portarsi verso ωh in A) il battistrada si comprime, STRISCIA e rallenta; nel secondo tratto (cioè nella fase in cui riaccelera passando da A per portarsi verso la zona indeformata), il battistrada si estende, STRISCIA e riaccelera. Ma sempre striscia.
Il punto A, quindi, NON è il centro di istantanea rotazione (quello che prima abbiamo chiamato C) della ruota. Il nostro centro di istantanea rotazione, infatti, NON è più sul piano stradale, ma SOTTO il piano della strada! Il mio C sta sotto A!
E tanto più la mia pancia è pronunciata, tanto più in basso andrà C, tanto maggiore sarà lo strisciamento del battistrada in A.
Prima considerazione. Questo è il motivo per cui i pneumatici si consumano: perché strisciano sull’asfalto. Anche se decideste di non fare più curve per il resto dei vostri giorni di guida, consumereste le gomme ugualmente. Ora, è chiaro che il valore di h (cioè del raggio sotto carico) dipende da un sacco di fattori, alcuni dipendenti dal pneumatico (come la struttura della carcassa, dallo stato di usura del pneumatico stesso, etc), altri dipendenti dalle condizioni di impiego (pressione di gonfiaggio, carico, velocità, etc). Per esempio, i pneumatici radiali hanno valori di h minori rispetto ai pneumatici a tele incrociate a pari raggio indeformato R (può sembrare strano, ma è proprio così e dipende dal fatto che il radiale ha una maggiore flessibilità radiale; però hanno valori di Ro meno lontani dal valore di R, cioè il raggio di rotolamento è più prossimo al valore del raggio indeformato).
Però deve essere ben chiaro che, anche se gonfiate tantissimo le gomme, anche se riducete il carico sul pneumatico, comunque, avrete un valore di h inferiore rispetto al valore del raggio di rotolamento e al raggio R indeformato. Cioè, una deformazione ce l’avrete sempre.
Poi, è chiaro che se aumentate il carico o riducete la pressione di gonfiaggio avrete una diminuzione di h e del raggio di rotolamento, mentre vi capiterà il contrario se gonfiate tanto o riducete il carico.
Seconda considerazione: la velocità angolare ω di una ruota dotata di pneumatico è SEMPRE MINORE di una ruota perfettamente rigida (per esempio, che so, di acciaio: un cerchione, tanto per fare un esempio che possiate capire tutti) con pari raggio sotto carico (cioè h, altezza del centro ruota dal suolo) e pari velocità di traslazione (V).
Afferrate bene questo concetto, perché sta alla base di tutto il resto: dalla motricità alla frenatura al funzionamento dell’ABS (lo vedremo!) alla resistenza la rotolamento.
Resistenza al rotolamento.
Abbiamo detto finora che, anche in assenza di coppie frenati o quant’altro, una ruota in condizioni di rotolamento puro offre una resistenza, cioè occorre spendere energia per trascinarla. Gli effetti di questa resistenza si traducono nello spostamento in avanti della risultante Z delle pressioni (che generalmente si indicano con la lettera greca σ, sigma) agenti sull’area di contatto del battistrada col terreno rispetto all’asse della ruota; tanto più avanti quanto più grande è il valore della resistenza al rotolamento.
Come potete vedere dalla figura sottostante, la mia risultante Z è spostata in avanti, (nel senso di moto) rispetto all'asse ruota, della distanza Δx.
Ciò dunque, dà luogo ad un momento resistente pari a Z Δx, dove Δx (che si legge “delta x”) altro non è se non la distanza del punto di applicazione di Z dall’asse della ruota.
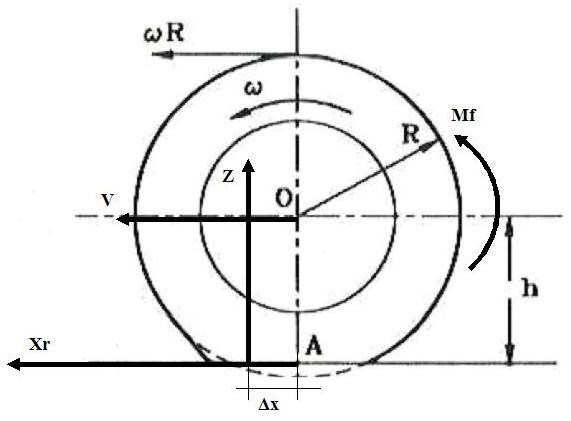
La resistenza al rotolamento, quindi, dipende dall’isteresi del pneumatico, cioè dalla impossibilità del pneumatico di restituire TUTTA l’energia che gli diamo per rotolare deformandosi. Ma non basta. Sappiamo anche che, in ogni caso, quando un pneumatico rotola, il battistrada striscia sull’asfalto (e il centro di istantanea rotazione C, che nella ruota rigida indeformata è nel punto di contatto tra ruota e strada, si sposta AL DI SOTTO del piano stradale).
Bene, aggiungiamo che la resistenza di rotolamento è dovuta PER LA MAGGIOR PARTE all’isteresi e solo per una minima parte (meno del 10%, tanto per intenderci) allo strisciamento, alla resistenza aerodinamica e ad altri fattori (tipo l’attrito del mozzo ruota nel centro della ruota).
Ora, guardate sempre bene la figura soprastante.
L’equilibrio alla rotazione mi permette di calcolare la resistenza al rotolamento.
La formula, è questa:
Xr = (-ZΔx + Mf)/h
Mf è il momento di attrito del mozzo ruota. Vale la pena di notare che Mf è NEGATIVO,
cioè nella formula riportata ha il segno positivo dal punto di vista algebrico. ma in realtà è negativo. Quindi la formula diventerebbe:
Xr = (-ZΔx - Mf)/h ossia -(ZΔx + Mf)/h
Ora, solo le ruote folli si trovano in questa situazione come nel disegno illustrato.
Se le ruote sono motrici, infatti, viene applicato un momento motore che deve quantomeno equilibrare i momenti ZΔx e Mf e in più fornire una trazione pari alla somma delle forze Xr, della resistenza aerodinamica e di tutte le altre eventuali dissipazioni di energia. Quindi, in caso di ruota motrice, devo scrivere, invece di Mf, la differenza tra il momento motore applicato (Mm) e il MODULO di Mf. se questa differenza è maggiore di ZΔx, la forza Xr è positiva (perché esercito una trazione, mi muovo e ho resistenza...).
In definitiva, dovete considerare il momento Mf con verso opposto per quello che concerne il nostro ragionamento...e quindi mettere il segno meno (-) nella formula.
La formula: Xr = (-ZΔx + Mf)/h
ha una utilità pratica piuttosto limitata perché è difficile determinare sperimentalmente sia Δx sia Mf.
Ai fini pratici, che sono quelli che c’interessano, la resistenza al rotolamento si esprime con una formula più pratica. Questa:
Xr = - f Z
dove:
- f è il coefficiente di rotolamento ed è molto simile (almeno concettualmente) al coefficiente di attrito; anzi, è un coefficiente di attrito e deve essere misurato sperimentalmente
- Z è la reazione vincolare del terreno alla forza normale. Per noi, e per farla semplice, è la reazione dovuta al peso. Cioè, è il peso che grava sulla ruota. Continuo ad usare Z perché voglio che sia chiaro che è uguale al peso solo in condizioni statiche, in piano. Se siamo su un piano inclinato (in montagna, per esempio) o stiamo accelerando o frenando (dove si devono tenere in considerazione anche i trasferimenti di carico) questo non è più vero.
Il segno meno indica che è una resistenza (quindi, che si oppone al moto): il coefficiente di rotolamento, infatti, per tradizione viene considerato positivo.
Il coefficiente di rotolamento dipende da un gran numero di parametri, quali la velocità di marcia (V), la pressione di gonfiaggio, il carico Z, le dimensioni della ruota, il tipo di fondo stradale, la struttura e il materiale che costituiscono il pneumatico.
Tutte cose, insomma, già scritte in precedenza.
Adesso, alcuni di questi parametri li analizziamo più in dettaglio.
Per esempio, vediamo di analizzare meglio gli effetti della velocità di marcia (V) sul rotolamento: come influenza il rotolamento?
Beh, credo che sia facile da intuire: al crescere della velocità, la resistenza (al rotolamento) aumenta. Però la resistenza NON cresce in modo lineare con la velocità (insomma, con una formula del tipo f = m V), ma in modo NON lineare: dapprima cresce lentamente; poi in misura molto marcata.
La formula che esprime questo andamento è la seguente, ed è molto importante:
f = f0 + k V2
I valori di f0 e di k vanno ricavati caso per caso da prove sperimentali.
Sostituiamo f nella prima formula e avremo:
Xr = (f0 + k V2) Z
Cioè
Xr = f0 Z + k Z V2
Cioè due termini: uno costante e uno funzione della velocità al quadrato.
L’andamento del coefficiente di rotolamento in funzione della velocità è riportato nella figura qui sotto. con due curve: una per un pneumatico radiale; una per un pneumatico convenzionale a tele incrociate.
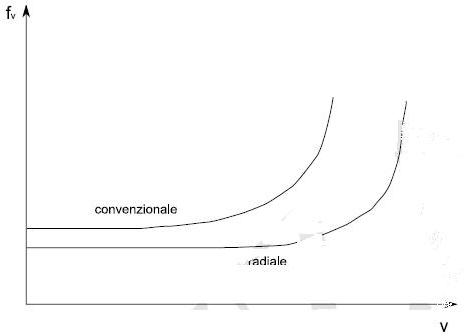
Si vede che, per entrambi i tipi di pneumatico, il coefficiente ha un andamento lentamente crescente fino ad una certa velocità; poi, si nota un "ginocchio" nella curva (in entrambe le curve: in una più evidente, segno di una minore linearità di comportamento; nell'altra meno evidente, segno di una maggiore progressività di comportamento) oltre il quale il coefficiente di rotolamento subisce un incremento repentino che porta a fargli assumere valori decisamente alti e rapidamente crescenti.
La velocità alla quale la curva presenta un “ginocchio” viene indicato come “velocità critica” del pneumatico.
La presenza della velocità critica del pneumatico è generalmente spiegabile dai fenomeni vibratori che si verificano nel suddetto. In queste condizioni, si manifesta un aumento di resistenza concomitante con il generarsi di vibrazioni che, a partire dalla zona di contatto del pneumatico con la strada, fanno sì che questo si stacchi dal terreno (nella parte posteriore della zona di contatto) e che hanno una lunghezza d’onda pari circa alla lunghezza della zona di contatto con la strada.
Insomma, la velocità critica è quella velocità alla quale i fenomeni vibratori (le vibrazioni) iniziano a manifestarsi e il pneumatico smette di funzionare in modo regolare.
La velocità critica dei pneumatici per auto è compresa tra 100 e 130 Km/h circa (dipende dal tipo di pneumatico e dalle sue caratteristiche, però più o meno cade lì...)
Potete benissimo individuarla anche sulle vostre auto, anche se avete i pneumatici perfettamente bilanciati: c'è una velocità, in quel range menzionato, in cui il pneumatico incomincia a vibrare leggermente, e voi lo sentite benissimo. Superata la velocità critica il pneumatico, poi, si stabilizza (è come la teoria sui rotori, insomma un po' come la lavatrice che vibra di più quando va piano e poi, al crescere della velocità di rotazione si stabilizza): in pratica, il primo modo di vibrare del pneumatico viene superato e le cose si stabilizzano.
Altri parametri che influenzano il coefficiente di rotolamento sono:
Struttura del pneumatico: la natura del materiale con cui sono fatti i pneumatici ha notevole importanza. Per esempio, tra un pneumatico normale, uno da vettura sportiva e una da corsa, quello da corsa avrà un ginocchio ben più in alto e la sua curva sarà ben più “lineare” del pneumatico da vettura normale…
Temperatura di funzionamento: al crescere delle temperatura di funzionamento, diminuisce lo smorzamento del pneumatico; di conseguenza diminuisce la resistenza, che è in gran parte dipendente dall’isteresi del pneumatico. Il pneumatico, insomma, tende ad un equilibrio stabile: un aumento della temperatura fa diminuire l’energia dissipata e quindi la produzione di calore; quando cala la temperatura, l’energia ricresce e quindi anche la produzione di calore, che fa però aumentare la temperatura che a sua volta farà ridecrescere l’energia dissipata, etc etc. si arriva ad una condizione di equilibrio.
Pressione di gonfiaggio: un aumento della pressione di gonfiaggio provoca una diminuzione del coefficiente di rotolamento. E così pure una riduzione del carico sul pneumatico. Il motivo è semplice: riducendo il carico o aumentando la pressione il pneumatico si deforma meno, con tutto quello che ne consegue.
Ecco perché è meglio gonfiare le gomme alla pressione giusta (o anche qualche decimo in più) piuttosto che sgonfiarle…e soprattutto, quando andate in ferie con la macchina carica, GONFIATE LE GOMME!
Dimensioni del pneumatico: i parametri principali sono il raggio del pneumatico (quindi le sue dimensioni) e il rapporto d’aspetto (es: il valore 60 nella misura 195/60 R 14) che indica il rapporto tra larghezza (del battistrada) e “spessore” radiale
Un aumento di entrambi, contemporaneamente, produce una diminuzione del coefficiente di rotolamento ed un aumento della velocità critica.
Ecco dunque una ragione in più per non mettere pneumatici super ribassati sulle vostre auto, che, tra l’altro, sono anche meno confortevoli, più fragili, meno progressivi, etc.
Riguardo al raggio, diciamo che un aumento del raggio ha effetto soprattutto sulla velocità critica, perché a bassa velocità la differenza è minima (ecco perché sulle utilitarie si mettono ruote “piccole” senza problemi).
Anche un aumento del rapporto tra larghezza del battistrada e altezza del pneumatico, a pari rapporto d’aspetto, è favorevole perché porta ad una maggiore rigidezza dei fianchi e quindi una minore dissipazione per isteresi.
Tipo di fondo stradale: diciamo che sul ghiaccio e sul cemento ad agosto, le cose sono un po’ diverse, o no? In prima approssimazione, basta traslare la curva f = f0 + k V2, facendo variare il valore di f0, che equivale a traslare la curva sull’asse delle ordinate (la alzo o l’abbasso, insomma).
Effetto del camber ruota: se la ruota non è dritta, ma ha camber, una parte di quella spinta (momento di autoallineamento, poi vedremo) contribuisce ad aumentare la resistenza al rotolamento e quindi ad aumentare il coefficiente di rotolamento.
Coast down di un veicolo.
Tenete presente la relazione Xr = f0 Z + k Z V2.
Questa è una relazione utilizzabile (a differenza di quella precedente, che era di difficile impiego). Si possono determinare i coefficienti f0 e k dei pneumatici. Ma questi valori interessano solo i costruttori di pneumatici (Michelin, Pirelli & Co).
Chi fa auto è interessato a conoscere, principalmente, altri parametri; ossia, è interessato alla resistenza complessiva (almeno, noi della sperimentazione)…
Ma, implicitamente, “pesa” anche l’effetto della resistenza al rotolamento.
Come?
Semplice: con le prove di coast down. Queste prove (dette sinteticamente “coast down”) sono una delle prove più importanti e più utili tra quelle che vengono fatte, perché permettono di conoscere un sacco di cose. Per esempio:
- sono alla base delle prove di omologazione (quindi, spesso i coast down vengono fatti alla presenza di un funzionario della motorizzazione);
- servono per provare la macchina sul banco a rulli (perché definiscono la curva di resistenza all’avanzamento della vettura);
- permettono di confrontare due vetture e di scoprire eventuali problemi (che so, un problema al cambio che assorbe troppa potenza);
- permette anche di determinare, con buona (direi anche ottima) approssimazione la potenza fornita dal motore;
- consentono di confrontare differenti tipi di pneumatici (e scegliere il migliore dal punto di vista del rotolamento), etc.
Insomma, ripeto: sono prove molto utili. Tanto utili che sono utilizzate da TUTTI i costruttori, TUTTI i produttori di pneumatici, molti fornitori e, persino, molte riviste (almeno, tra quelle che “misurano” le auto).
Tutto nasce dagli americani, negli anni ’40 (se non vado errato).
Come sapete, il limite di velocità, in America, è di circa 50 mph, equivalenti a circa 90 Kmh.
In America, venne “normata” (cioè messa a norma) una prova per la determinazione della resistenza all’avanzamento.
In pratica, gli americani chiamarono “TEMPO di coast down” il tempo impiegato da una vettura (dalla vettura di cui mi interessa conoscere il coast down) il tempo impiegato per passare da circa 95 Km/h a 85 Km/h. In pratica, sono “a cavallo” dei 90 Km/h della velocità limite (da codice). Capite benissimo che, se conosco questo tempo, conosco in pratica la forza media che si oppone al moto a 90 Km/h.
Il perché è semplice e dipende dalla formula F = m a = m ΔV/Δt
Ora:
m è la massa della vettura, che conosco
ΔV è la differenza di velocità, che ho imposto (10 Km/h, cioè 95-85 Km/h)
Δt è il tempo per rallentare di quel ΔV (10 Km/h), che conosco perché l’ho appena misurato.
Quindi, conosco la forza MEDIA che si oppone al moto, a 90 Km/h.
Andando avanti, è chiaro che, se io tendo a far diventare sempre più piccolo quel ΔV, approssimandomi sempre più ad un dv, in pratica, tendo al “limite” di quella formula. Quindi, la mia forza sarà sempre meno MEDIA e sempre più istantanea.
In pratica, riduco sempre più la differenza di velocità e misuro il tempo per passare da V+dV a V e da V a V-dV….
E misuro il tempo, istante per istante.
Se faccio questo non solo “nell’intorno dei 90 Km/h” ma anche alle altre velocità, riesco ad ottenere una curva.
In pratica, oggigiorno, prendo la macchina (naturalmente perfettamente “a posto” sia come angoli, sia come pressione gomme, sia come assetti, sia come tutto il resto…), la lancio a circa 120-130 Km/h e, a quel punto, la faccio rallentare in folle fino a quando non si arresta completamente. Registro la velocità, (a step di 1 Km/h che è l’intervallo ritenuto sufficiente) il tempo, lo spazio percorso e, con pochi, semplici calcoli, ottengo una curva di decelerazione. Rifaccio la prova un numero sufficiente di volte, per avere una corretta precisione statistica, e faccio una interpolazione delle curve così ottenute.
La curva che ottengo è la mia decelerazione “istantanea”, ossia: per qualunque velocità (ovviamente tra 0 e 120 Km/h) conosco la decelerazione a quella velocità….quindi, se moltiplico per la massa dell’auto, ho la curva di resistenza all’avanzamento. Ossia, ad ogni velocità, conosco quanto vale la resistenza all’avanzamento.
Naturalmente, questa curva può essere descritta con una polinomiale…
A noi, basta arrivare ad un polinomio del secondo ordine (la resistenza è proporzionale al quadrato della velocità), ottenendo una relazione del tipo:
F = F0 + F1 V + F2 V2
Ora, per motivi di semplicità, bastano 2 coefficienti, F0 e F2 (F1 lo mettiamo uguale a zero) per avere la nostra curva. Quindi, la formuletta di prima si traduce in:
F = F0 + F2 V2
I due coefficienti F0 e F2 (costante e quadratico) sono quelli che descrivono la mia vettura!
Diamo loro un senso.
Riprendiamo la già nota formuletta della resistenza la rotolamento del pneumatico:
Xr = f0 Z + k Z V2.
Anche qui ho un termine costante e uno quadratico
Quindi, il mio F0 rappresenterà, chiaramente, la parte di rotolamento; l’F2 rappresenta il contributo dovuto alla velocità (al quadrato della velocità): in pratica, il contributo dell’aerodinamica, principalmente.
Certo, dentro al mio F2 ci va anche il termine k Z dell’espressione che si riferisce alla resistenza al rotolamento; ma questo è talmente “piccolo” in peso, rispetto al contributo dovuto all’aerodinamica (in termini matematici si dice che è un infinitesimo di ordine superiore), che lo posso anche trascurare.
Nell’F0, invece, ci cade proprio il mio f0 della resistenza al rotolamento. Ma, nella resistenza al rotolamento, ci va dentro pure – che so - l’attrito dei mozzi ruota (cuscinetti & Co), il contributo dovuto al roll back delle pinze freno, etc. (però, la coppia frenante Mf dovuta al mozzo ruota l’abbiamo già vista ed è stata già oggetto di ampia discussione).
Insomma,
F0 “pesa” il rotolamento
F2 “pesa” l’aerodinamica
Quindi, se sto provando delle gomme e voglio vedere quale delle gomme che sto provando è più scorrevole, quale coefficiente vado a guardare (perché sono sicuro che cambierà)?
Bravi, il mio F0!
Invece, il mio F2, sono certo, cambierà di pochissimo.
Tanto per darvi un’idea dell’ordine di grandezza dei coefficienti qui descritti, vi riporto i valori di F0 e F2 di una vettura qualunque.
F0 = 215 [N]
F2 = 0,0405 [N/(Km/h)2]
Il peso di F2 (cioè dell’aerodinamica) comincia a farsi sentire oltre i 100 Km/h (esattamente come è giusto che sia; ricordatevelo, dunque: l’aerodinamica diventa importante, per la resistenza oltre i 100 Km/h; sotto, conta di più il rotolamento, gli attriti, etc. Questo vale anche per le vostre considerazioni sui consumi di carburante).
Forze scambiate tra ruota e strada.
Fondamentalmente, le forze che la ruota scambia con la strada possono essere suddivise in forze scambiate in senso longitudinale (in pratica, frenata e trazione) e forze scambiate in senso trasversale (le forze che generano la “tenuta di strada”).
Riprendiamo la nostra ruota di prima. Purtroppo non posso riprendere il disegno di prima perché la ruota forma una gobbetta davanti al punto in cui inizia il contatto con la strada che potrebbe trarvi in inganno. Sono quindi costretto a prendere un altro disegno, simile a quello precedente. In pratica qui ho applicato, nel giusto verso, il momento frenante (la coppia frenante) che chiamo Mb. Stavolta, il senso di Mb è quello giusto.
Anche il verso della forza frenante Fb è giusto. Fb è la forza frenante che è applicata nel punto a terra.
La velocità angolare (di rotazione) della ruota, che prima avevamo indicato con ω (omega minuscolo, che in greco si dice omicron), adesso viene indicata con Ω (omega, maiuscolo).
Attenzione bene a questo fatto: gli elementi della fascia di battistrada che entrano in contatto col terreno adesso sono in TENSIONE, mentre prima (nella ruota in rotolamento puro) erano in compressione.
La velocità periferica della ruota (relativa al suo centro O), che nella ruota in rotolamento puro era ωR0 e variava tra R e h, adesso è maggiore. Cioè, il raggio di rotolamento R0, che nella ruota in rotolamento puro era compreso tra h e R, ora si sposta verso R e, al crescere di Fb (cioè della forza frenante) diventa MAGGIORE di R!!!
Di conseguenza il centro di istantanea rotazione C, che nella ruota in rotolamento puro era di poco sotto il piano stradale, si porta ad una maggiore profondità!
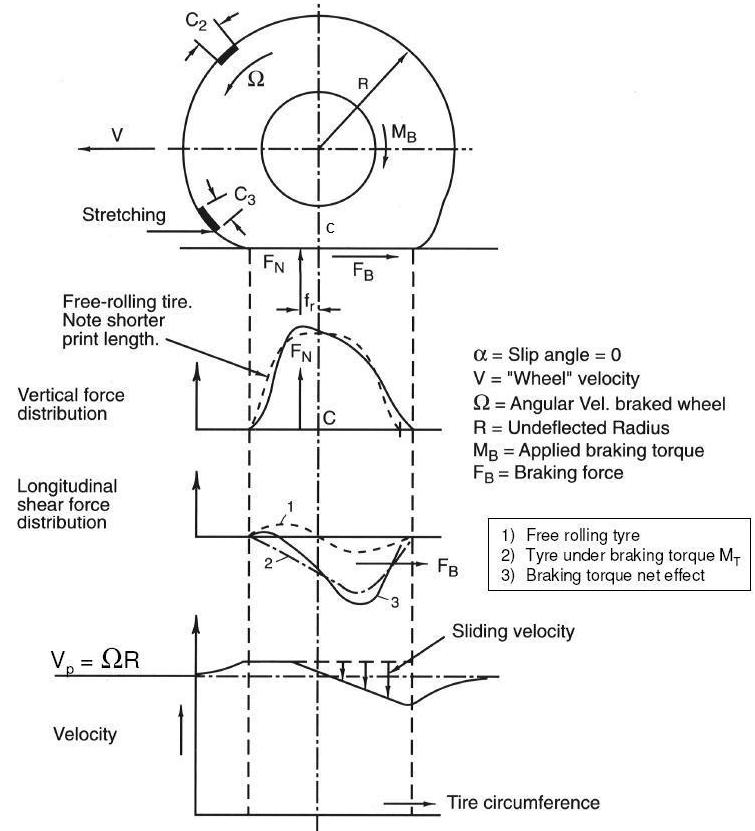
Osservate la figura seguente: al crescere della forza frenante, aumenta la profondità di C (da C a C’ nella figura).
Nel caso in cui la ruota, anziché frenata, sia motrice, il centro di istantanea rotazione C, invece, si colloca AL DI SOPRA DEL PIANO STRADALE (da C a C” nella figura).
Questo è molto importante: dove si sposta il centro di istantanea rotazione in caso di frenatura e in caso di trazione.
Ora, in caso di ruota frenata, la velocità angolare della ruota (nella figura di prima indicata con Ω) sarà MINORE della velocità angolare della ruota indeformata di raggio h.
Invece, nel caso di ruota di trazione, la velocità angolare della ruota (nella figura di prima indicata con Ω) sarà MAGGIORE della velocità angolare della ruota indeformata di raggio h.
Adesso, introduciamo il concetto di scorrimento.
Avete presente che cos’è una sgommata? Bene, lo scorrimento è il termine tecnico con cui si “spiega” la sgommata. (spiegandolo con termini alla buona).
Allora, si definisce scorrimento (percentuale), indicato con la lettera greca sigma (σ), della ruota come
σ = (ω/ ωc) – 1 cioè σ = - v/V dove
v è la velocità di spostamento del punto di contatto della ruota con il suolo;
V è la solita velocità del centro O.
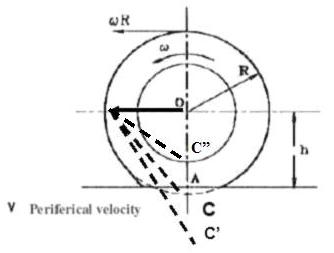
Guardando la figura successiva capirete meglio sia la posizione del centro di istantanea rotazione in frenata e in trazione; sia la definizione dello scorrimento percentuale, qui definito come S.
Non fatevi prendere dal panico, le formule sono identiche a quelle di prima…
ωR è la velocità v
e
V è sempre la velocità di O
Il valore di S (o di σ, come volete chiamarlo) è compreso tra 0 e 1 o, se lo mettiamo in termini percentuali, tra 0 e 100 %.
Scorrimento = 0% significa che la ruota è in rotolamento puro
Scorrimento = 100% significa che la velocità del punto C (centro di istantanea rotazione) è uguale a quella del punto O (centro della ruota), cioè che il punto C si trova ALL’INFINITO rispetto al piano stradale, cioè ancora che:
1) Ho le ruote bloccate (in caso di frenata);
2) Sto facendo un “burn out” (senza però muovermi) in caso di trazione.
Rispetto alla condizione iniziale quindi se definiamo C’ il nuovo centro di istantanea rotazione. esso si troverà nei due casi rispettivamente sotto o sopra a C.
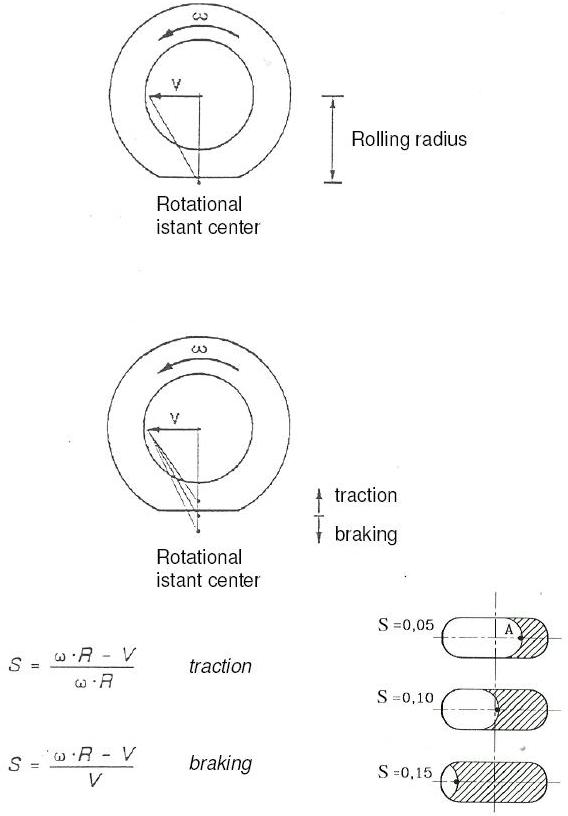
La presenza di una velocità di slittamento (la v, che è indicata anche come ωR) NON significa che TUTTA la zona a contatto con la strada stia slittando. Nella prima parte del contatto tra battistrada e suolo, non si ha slittamento. Solo in un (più o meno) limitato tratto di battistrada prima del punto C si ha slittamento, perché la velocità tende a diminuire e quindi si ha lo slittamento. Questa zona tenderà a crescere al crescere del valore di S (detto anche σ). e solo in caso di scorrimento percentuale 100% TUTTA la fascia di battistrada a contatto col terreno sarà in slittamento.
Ora, la forza Fb (forza frenante) è funzione di questo slittamento. ma anche la forza di trazione (che è la stessa cosa, solo vista al contrario).
Per chiarire meglio gli ultimi concetti, proviamo a riassumere così. Osservate la prossima figura.
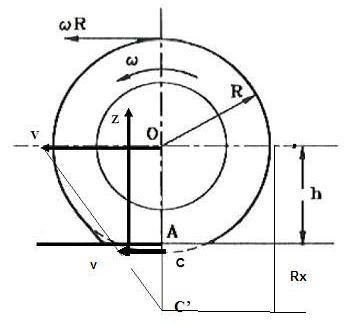
Convenzionalmente, si parla di rotolamento puro quando alla ruota NON ho applicato alcuna coppia, né motrice né frenante.
In questo caso, fissato un certo carico verticale Z e la velocità V del centro O della ruota, il cerchio ruoterà con una certa velocità angolare pari a ω = V / R0
Il valore di R0 può essere CALCOLATO solo con la formula qui sopra. E basta.
Dove R0 è il raggio della ruota in condizioni di rotolamento puro ed è compreso tra h (altezza da terra del centro ruota O) e R (raggio della ruota inderformata).
Quindi, in condizioni di puro rotolamento, il centro di istantanea rotazione C si trova (leggermente) al di sotto del piano stradale.
Tanto per darvi un’idea, un valore indicativo di dove si trovi C è dato da h/R0 = 0,95, cioè poco sotto il piano stradale… Ricordo che R0 è il raggio (= la distanza) tra C e O…
Se, invece, applico una coppia diversa da 0, cioè se applico una coppia motrice o frenante, questa condizione porta ad una velocità angolare Ω della ruota diversa da ω e quindi ad un riposizionamento del centro di istantanea rotazione da C a C’ che, nel caso specifico di frenata, verrà a trovarsi ad una distanza Rx = V / Ω. Al contrario, in caso di applicazione di una coppia motrice, si riposizionerà AL DI SOPRA del punto C.
In queste condizioni di funzionamento, il punto C della ruota andrà ad avere una VELOCITA’ DI SCORRIMENTO che indichiamo con v. La velocità di scorrimento v varrà:
v = V – Ω R0
A questo punto, sempre nel caso di una coppia frenante, si definisce una grandezza detta scorrimento che, diciamo così, dà l’idea dello “slittamento” di C (e quindi della velocità con cui “striscia”), fatta 100 la velocità del centro ruota O.
Lo scorrimento vale σ = v / V ossia, se metto dentro la formula precedente,
σ = (V – Ω R0) / V = 1 – (ωR0 / Ω R0) cioè 1 - ω / Ω
le stesse relazioni valgono in caso di ruota a cui venga applicata una coppia motrice: semplicemente, si invertirà il segno di σ.
Coefficiente di aderenza.
La forza Fb (riportata in precedenza) che la ruota trasmette al suolo, è funzione dello scorrimento: vale 0 (zero) quando lo scorrimento è nullo (cioè quando la ruota rotola e basta) e cresce in modo piuttosto rapido.
Aggiungiamo anche che cresce fino ad un certo punto, fino a toccare un massimo, e poi diminuisce in modo più o meno pronunciato.
Diciamo che, in prima approssimazione, possiamo ritenere che la forza frenante Fb sia proporzionale, a parità di scorrimento, al carico verticale Z.
Quindi, abbiamo detto DUE cose importantissime:
la forza Fb dipende:
1) dallo scorrimento (percentuale)
2) dal carico verticale sulla ruota.
Si può perciò definire un coefficiente di aderenza (che si chiamerà coefficiente di aderenza longitudinale) μx che vale
μx = Fb / Z
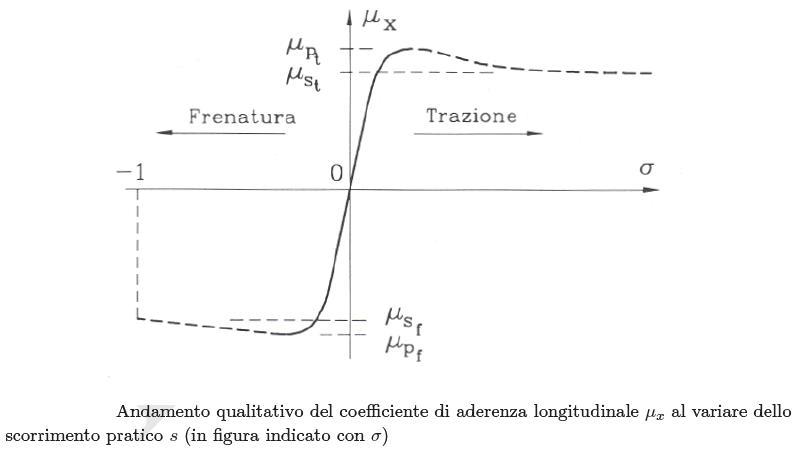
Come vedete dal grafico, la curva del coefficiente di aderenza, funzione dello scorrimento, è praticamente simmetrica rispetto all'origine degli assi.
i valori in cui sigma (σ) è negativo sono le condizioni in cui sulla ruota agiscono momenti frenanti; quelli in cui sigma (σ) è positivo significano che sulla ruota sta agendo una coppia motrice.
In pratica, però, le due curve, quella "negativa" e quella "positiva", sono uguali come andamento.
Allora, per facilitarvi di più le cose, possiamo ragionare solo su una delle due, ricordandoci poi che le stesse considerazioni possono valere anche per l'altro lato della curva.
Per esempio possiamo "segare" via tutto ciò che è negativo e ragionare solo sulla curva che è disegnata nel primo quadrante dove sia σ, sia il coefficiente di aderenza μ sono positivi.
Ecco dunque la curva (unica) su cui andremo a fare i nostri ragionamenti (qualitativi).
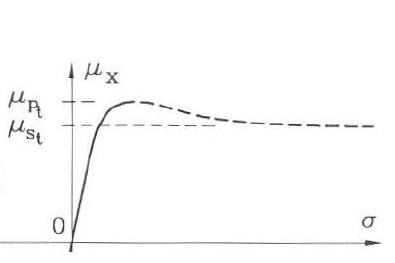
Il primo tratto della curva riporta una crescita molto rapida del coefficiente di aderenza; dopodiché si arriva ad un valore massimo e poi, un calo, più o meno repentino, del coefficiente.
I valori di scorrimento percentuale attorno a cui si ottiene il massimo coefficiente di aderenza variano nell'intorno del 15% (valori variabili in funzione di moli parametri, che poi vedremo e, soprattutto, delle caratteristiche del pneumatico; in ogni caso, diciamo che si sta attorno a quel 15%).
Oltre il massimo, la curva ha un ginocchio e poi ridiscende.
Consideriamo, allora, una ruota cui sia applicato un momento frenante. In questo caso, sia μ sia σ sono negativi, ma sulla nostra curva hanno entrambi valori positivi: basta solo che ci si ricordi che siamo in condizioni di frenatura (per il caso di ruota in trazione, varranno le medesime considerazioni).
I tratti di curva compresi tra i valori di coefficiente di aderenza μpt e μst (quelli tratteggiati nella figura; in pratica, dal ginocchio in avanti) sono, nell'uso pratico dell'auto, zone di funzionamento INSTABILE. sono zone di instabilità.
Per capirlo, bisogna prendere l'equazione del moto della ruota. Sarà:
J dω/dt = Fb h – Mb (*)
In pratica, ho fatto l’equilibrio dei momenti.
- J è il momento polare d’inerzia della ruota rispetto ad O (all’asse principale d’inerzia che passa per O);
- ω è come sempre la velocità angolare della ruota;
- Fb e Mb sono, come bene sapete, la forza frenante (applicata nel punto di contatto tra battistrada e ruota) e il momento frenante (dato dalla pinza freni).
(*) Non spaventatevi della formula: in pratica, ho trasformato la F = m a (o, meglio, la F = m dv/dt) per i moti rotatori semplicemente sostituendo alle forze i momenti; alla massa il momento d’inerzia e alla velocità la velocità angolare. Niente di speciale, dunque.
Nel tratto che abbiamo considerato instabile, una diminuzione della velocità ω a velocità V costante, cioè un aumento di σ, porta ad una diminuzione del valore assoluto di Fb (cioè della forza frenante) che è la forza CHE MANTIENE LA RUOTA IN ROTAZIONE (guardate bene la figura)!
Se questa diminuzione di Fb non è accompagnata da una conseguente diminuzione del momento frenante Mb, ne consegue un ulteriore rallentamento della ruota, accompagnato da una ulteriore riduzione di Fb e così via.
Insomma, in un attimo, si arriva la bloccaggio della ruota perché ho un alto valore di Mb ma un basso valore di Fb e questo squilibrio comporta il bloccaggio delle ruota!
In parole più chiare, una volta che ho superato il valore ottimale di σ (il valore massimo), si arriva rapidamente al completo bloccaggio della ruota.
Dico di più: finché mi trovo nel tratto “in salita” della curva, ad ogni aumento di σ ho un aumento del coefficiente di aderenza e quindi posso aumentare anche il mio momento di bloccaggio, cioè posso “pinzare” ancora di più sui freni; quando supero il valore di σ ottimale, mi può succedere ciò che ho detto nel caso in cui non diminuisco il momento frenante Mb.
Ora, non è realistico pensare che un guidatore non professionista sia in grado di dosare la frenatura in questo modo, ossia in modo da impedire che avvenga il bloccaggio, e anche i guidatori professionisti (piloti, collaudatori, etc) devono essere molto attenti. Ecco perché si ricorre ai dispositivi antibloccaggio ABS.
L’ABS, dunque, lavora su questo principio, su questa formula e, tanto per essere più chiari, nella zona di funzionamento del pneumatico indicata nel tratteggio (μpt – μst)
In pratica l'ABS rileva la decelerazione della ruota e, in funzione di questa, attua una riduzione del momento frenante Mb (agendo sulla pressione idraulica dell'impianto per ogni singola ruota) quando la decelerazione supera un valore prefissato. Una volta ripristinata la condizione di funzionamento corretta, col giusto valore di Mb in funzione dello scorrimento percentuale, il funzionamento dell'ABS cessa; ma si possono allora ripresentare le condizioni partenza, col rischio di bloccaggio, che determinano un nuovo intervento dell'ABS e così via. Il risultato è una serie rapida di interventi con una variazione ciclica delle velocità della ruota interessata.
La migliore azione dell’ABS si ha quando il sistema "monitora" TUTTE le ruote singolarmente (mi sembra ovvio: ogni ruota ha condizioni di aderenza e funzionamento differenti dalle altre) e quando le ruote sono "libere" (cioè, ad esse NON vengono applicate coppie che non siano la coppia frenante della pinza freni), quindi prive di coppie motrici. Questo è il motivo per cui su alcuni fuoristrada molto specializzati (es: Mercedes classe G) che prevedono il bloccaggio dei tre differenziali, all'atto del bloccaggio dei differenziali si disinserisce automaticamente l'ABS (se ho i differenziali bloccati, significa che le ruote sono tutte collegate tra loro e ogni azione su una ruota si ripercuote anche sulle altre); oppure, che ai tempi in cui l'Alfa correva nel DTM, la 155 V6 TI "apriva" (letteralmente) i differenziali (ricordo che erano controllati elettronicamente) per migliorare la frenata.
Insomma, per avere i migliori benefici, in vetture dotate di ABS bisognerebbe frenare (con intervento dell'ABS) e schiacciare la frizione (così tutte le ruote sono "libere").
Inoltre la forza frenante (o la trazione) che posso applicare alla ruota è funzione del coefficiente di aderenza (che varia come ben sapete) e della forza normale alla ruota (che, in piano, è il peso) secondo la (nota) formula: Fb = μ Z. Quindi, se ho dei trasferimenti di carico (cosa sono? poi lo vedremo), o comunque delle condizioni che mi facciano variare la forza sulla ruota, questi influiranno sulla frenata o sulla motricità della ruota.
Infine, ricordatevi che il massimo della trazione (e della frenata) avvengono per valori di scorrimento percentuale (σ) intorno al 15% (diciamo tra 13 e 20 %, cos' tanto per tenerci larghi): ciò significa che, per partire veloci occorre sgommare un po' ma non lasciarsi andare a fare delle sgommate eccessive e così pure nel frenare, occorre una leggera sgommatina (modulare la frenata per avere leggeri bloccaggi, corrispondenti al mio 15-20% di scorrimento). Se volete una conferma del lavoro dell'ABS, lanciatevi con la vostra auto a circa 70-90 Km/h e poi fate una bella frenata con intervento dell'ABS. Se avrete avuto l'accortezza di frenare su un fondo regolare e pulito, potrete vedere i segni delle "sgommatine" dovute al ciclare dell'ABS: quelle sgommatine sono, appunto, la dimostrazione tangibile del 15-20% di scorrimento.
Considerazioni.
Come abbiamo detto, e ormai dovremmo aver ben chiaro, l’aderenza (longitudinale) del pneumatico dipende dal peso (guardate che è un errore dire peso, se non siamo in piano; sarebbe meglio dire dalla forza normale al piano del pneumatico) e dal coefficiente di aderenza che ha l’andamento che abbiamo visto nel disegno precedente.
Il coefficiente di aderenza longitudinale dipende a sua volta da differenti parametri, quali il tipo di pneumatico, le condizioni della strada, la velocità, LA FORZA LATERALE (cioè, se c’è un “impegno” del pneumatico in senso trasversale, come quando faccio una curva; cioè ancora se c’è un ANGOLO DI DERIVA: vedremo poi cos’è). Insomma, c’è una forte differenza tra le curve ottenute in differenti casi da differenti sperimentatori (proprio perché sono curve sperimentali: c’è poco di “teorico”, ma questo coefficiente viene rilevato sperimentalmente).
Per esempio, c’è una bella differenza tra pneumatici radiali e pneumatici convenzionali (a tele incrociate), con i radiali che offrono sempre un’aderenza migliore dei convenzionali; e, tra gli stessi radiali, tra i pneumatici tradizionali (detti in gergo “neri”) e quelli, moderni, a basso rotolamento, che fanno consumare poco (detti, in gergo, “verdi”). I neri sono migliori quanto ad aderenza, naturalmente!
Poi, c’è la dipendenza dalla velocità, a sua volta influenzata dalle condizioni ambientali: se vado sull’asciutto, al crescere della velocità vedrò una diminuzione modesta dell’aderenza; se sono sul bagnato, l’aderenza calerà di più (ricordatevelo quando guidate quando piove, significa che, sul bagnato, già tengo meno; sul bagnato, in velocità, tengo PARECCHIO meno!!). C’è l’usura del battistrada che, soprattutto ad alta velocità, ha parecchia influenza. Ma non nel senso che pensate voi: al crescere della velocità, il coefficiente di rotolamento AUMENTA su strada asciutta. Il perché mi sembra chiaro: ridurre l’altezza del battistrada (scolpito, nelle gomme stradali) significa aumentare la superficie dell’area di impronta a terra. Attenzione: ho scritto “su strada asciutta”, perché, invece, su strada bagnata, diminuisce. Soprattutto se lo spessore del velo d’acqua è notevole. In questo caso, infatti, può verificarsi un fenomeno si sostentamento idrodinamico chiamato acquaplaning.
In parole semplici, quando la pressione davanti alla ruota raggiunge il valore di sostentamento idrodinamico (in base alla semplice formuletta della pressione dinamica ½ ρ V2), allora il pneumatico “galleggia” sulla strada. Ora, la pressione di sostentamento idrodinamico dipende, a sua volta, direttamente dalla pressione di gonfiaggio del pneumatico (oltre naturalmente dalla velocità di marcia) e quindi, se voglio ridurre la possibilità di aquaplaning devo gonfiare di più le ruote: sposterò più in alto il punto in cui si manifesta il fenomeno. La cosa è abbastanza intuibile anche in modo più semplice: gonfio di più la ruota e quindi riduco l’area di impronta del pneumatico, quindi avrò carichi per unità di superficie (pressioni) maggiori.
Quindi, quando piove, gonfiare di più le gomme!
Tanto per darvi un’idea, il coefficiente di aderenza , che sul strada asciutta è di circa 1,1-1,15, in caso di aquaplaning può arrivare ad essere anche 0,05. Significa che appena penso di toccare il freno, sono già con le ruote bloccate.
Per impedire il verificarsi della sostentazione idrodinamica, o almeno per ritardarla, bisogna evacuare l’acqua. Si può fare in due modi: o rendo la strada molto permeabile (asfalti drenanti) o scolpisco di più il pneumatico.
Attenzione: gli asfalti drenanti “tengono” molto meno sull’asciutto!
Perché? Perché siccome la “grana” della ghiaia di cui sono composti è maggiore, ci sono più spazi e la superficie di contatto tra battistrada e asfalto appunto si riduce. E, se riduco la superficie.
Bene, nel caso in cui la ruota sia motrice (cioè con coppia motrice) anziché frenata (cioè con momento frenate, come abbiamo discusso fin qui), valgono le stesse, identiche, considerazioni. Semplicemente, tenete presente che il coefficiente di aderenza μ adesso è positivo.
:grazie) alfistavero
Tratteremo qui di seguito l’argomento del pneumatico, cos’è, a cosa deve soddisfare, quali sono le sue caratteristiche.
Ma prima, introduco due considerazioni iniziali.
La prima, faceva parte di una delle domande chiave che l'ing. Forghieri (sapete chi è?) poneva ai neolaureati per vedere se era il caso di assumerli (sia in ferrari sia in Oral) o no.
Le ruote sono quei componenti attraverso cui la macchina è collegata al terreno. con cui, insomma, scambia forze per andare, fermarsi, curvare, accelerare, etc.
Perché ciò avvenga, LE RUOTE DEVONO GIRARE, DEVONO ROTOLARE!!!! se la ruota striscia (sgomma o scivola di lato) NON TRASMETTE ALCUNA FORZA!!!!
Questo deve essere ben chiaro.
Forghieri faceva una domanda di questo tipo: metteva una macchinina con le ruote posteriori bloccate (un modellino di F1) su un piano inclinato, la faceva scendere e questa, naturalmente, cadeva dal piano inclinato. allora chiedeva: "Perché succede questo?"
La risposta era: perché il posteriore non fa più tenuta....
Sembra una stupidaggine, ma vi posso assicurare che ne faceva fuori tante, di giovani promesse!
La seconda: la ruota trasmette (scambia) le forze tra terreno e veicolo. Bene. TUTTE le forze, diciamo così, "dissipative" (frenata, aderenza trasversale, resistenza all'avanzamento, le forze dovute agli ostacoli incontrati sulla strada, etc) sono applicate nella zona di contatto col terreno (A TERRA); TUTTE le forze motrici (conseguenza delle coppie motrici) sono applicate A CENTRO RUOTA.
Per cui, quando dovremo ragionare sugli effetti di una forza frenante, dovremo fare riferimento ai bracci a terra; quando parleremo di forze di trazione, dovremo considerare i bracci a centro ruota.
Tanto per chiarire meglio, guardiamo il disegno seguente.

Abbiamo:
- la forza N, che è NORMALE (cioè perpendicolare) al piano stradale. essa rappresenta la reazione vincolare della strada alla forza normale che agisce sulla ruota (nel nostro caso, visto che siamo in piano, questa è rappresentata dal peso che grava sulla ruota, oltre al peso della ruota stessa)
- la forza T, applicata al centro della ruota: è la forza di trazione conseguente alla coppia motrice data dal motore e applicata ai semiassi a centro ruota (la quale coppia, se la divido per il raggio della ruota mi dà la forza di trazione)
- la forza F frenante: è conseguenza del momento frenante generato dalle pinze freno. anche in questo caso, se divido il momento per il raggio della ruota ho la forza frenante.
- Infine, ho aggiunto anche i momenti (Mt è la coppia motrice; Mf è il momento frenante...). come vedete, i momenti ci sono, eccome. però i punti di applicazione delle forze di trazione e di frenatura sono differenti: la forza di trazione è applicata a centro ruota; la forza frenante al centro dell'orma di contatto.
Definizione di Centro della ruota e Asse di istantanea rotazione della ruota.
Osservate bene la figura sottostante.
Il punto O si chiama “centro della ruota” o anche “asse della ruota” (se pensiamo che quella disegnata è solo la vista laterale…).
La ruota è supposta in movimento, con una certa velocità parallela alla strada (la V rossa) applicata al suo asse di rotazione. La ruota dunque TRASLA con velocità V costante. Quindi si dice che l’asse della ruota ha un moto traslatorio uniforme.
Però, la ruota, oltre a traslare, ha anche un moto rotatorio attorno al proprio asse O e dunque ruota con velocità angolare ω, che dipende dalla velocità V e dal raggio della ruota stessa (ma anche da altri parametri che per adesso non introduciamo).
Insomma, a me interessa che sappiate cosa sia l’asse ruota e il centro ruota (che sono poi lo stesso punto, in un disegno); ma anche che cosa sia CENTRO (O ASSE) DI ISTANTANEA ROTAZIONE della ruota.

Se conosco V, in ogni istante, in realtà, la ruota “rotola” appunto attorno ad un punto (che è quello indicato con C) che è il punto di contatto della ruota con la strada. Insomma, in termini fisici si dice che in ogni istante si può definire un punto (o un asse) centro dell’atto di moto della ruota.
In parole più semplici, è solo il punto (o l’asse) attorno a cui la ruota rotola istante per istante…quindi il centro ruota O RUOTA anche lui attorno a questo punto, che rimane immobile: infatti, come vedete dal disegno, il punto O (centro ruota) ha una velocità (che è la velocità del centro ruota, la velocità di traslazione, quella indicata con la V rossa). Il punto C NON ha alcuna velocità: è fermo!
Quindi, riassumendo, abbiamo definito il centro ruota e il centro di istantanea rotazione (dell’atto di moto) della ruota: nel disegno, rispettivamente O e C.
Abbiamo visto il punto C, centro di istantanea rotazione della ruota. Bene: C è anche il punto di contatto tra la ruota e la strada. Osservate la figura qui sotto.
Guardate il caso ideale (a).
Nel punto di contatto tra la ruota e la strada viene applicata la forza N che è la reazione vincolare della strada alla forza NORMALE (cioè perpendicolare) applicata alla ruota. Nel nostro caso, visto che siamo in piano, questa forza normale altro non è se non la forza peso della ruota (il carico applicato alla ruota). Questa forza peso altro non sarà se non il peso della ruota + la parte del peso dell’auto che compete alla ruota. Se ho solo la ruota e basta, sarà solo il peso della ruota.

Bene: nel caso ideale, il contatto tra ruota e strada è puntiforme (il punto C).
Peccato, però, che nella REALTA’ le cose vadano diversamente.
In realtà, infatti, si tiene conto della deformabilità della ruota (cioè cerchio + pneumatico) e si ammette che il contatto del pneumatico con la strada non avvenga solo in un punto (il punto C), ma su una superficie limitata chiamata “orma di contatto” (o “superficie di contatto”). Questa superficie ha una sua propria grandezza, definita come “area dell’orma di contatto” (o “area della superficie di contatto”; o anche “area dell’impronta”).
A questo punto, ci aggiungiamo anche che il pneumatico NON è perfettamente elastico: quando io deformo il pneumatico per farlo rotolare, gli do una certa energia che, dopo la deformazione, quando il pneumatico tende a riprendere la propria forma, non viene interamente restituita. Parte di questa energia, viene persa a causa delle dissipazioni (delle perdite) all’interno del materiale.
Queste perdite sono dovute all’ISTERESI del materiale con cui sono fatti i pneumatici. Di conseguenza, si è visto sperimentalmente che per rotolare il pneumatico richiede di spendere una certa energia. Questo equivale ad una distribuzione delle pressioni la cui risultante è leggermente spostata in avanti nel senso del moto: guardate il disegno del caso reale (b) e confrontatelo con il caso ideale (a).
Come vedete, la forza N, che rappresenta la reazione vincolare della forza normale al terreno (nonché la risultante della distribuzione delle pressioni) è spostata in avanti rispetto al centro di istantanea rotazione. E guardate anche la distribuzione delle pressioni: nel caso ideale, tale distribuzione è simmetrica; nel caso reale, è asimmetrica con il picco verso l’avanti.
Questo rappresenta la spiegazione tecnica dell’isteresi del pneumatico. In pratica, anche senza applicare forze resistenti, la ruota, per rotolare, dissipa energia!
Naturalmente, l’energia persa è funzione della deformazione del pneumatico; quindi, delle caratteristiche costruttive del pneumatico stesso (tipo di materiale, tipo di pneumatico cioè se radiale o a tele incrociate; dimensioni del pneumatico, larghezza del battistrada, etc) e di caratteristiche esterne (pressione di gonfiaggio, carico verticale sul pneumatico, etc). Per esempio, i pneumatici “verdi” sono pneumatici realizzati con materiali “a bassa isteresi”, che si deformano poco; ma, per questo, “tengono” anche meno…
Chiaramente, tanto maggiore sarà l’isteresi del pneumatico, tanto maggiore sarà l’energia persa per il rotolamento, tanto maggiore l’energia necessaria per far rotolare il pneumatico…ciò equivale a “spostare” sempre più in avanti il punto di applicazione della forza N…
La coppia resistente (il momento resistente), rispetto al centro di rotazione O, sarà il prodotto della forza N moltiplicata per il braccio (la distanza del punto di applicazione di N) dal punto di contatto C: nel disegno, Mf = N u
Condizione di puro rotolamento.
Definiamo la condizione di puro rotolamento.
A livello intuitivo, possiamo capirla benissimo: la ruota rotola e basta.
A livello scientifico, diciamo che la condizione di PURO ROTOLAMENTO è quella in cui non sono applicate coppie all'asse della ruota (quello che abbiamo indicato nella figura precedente con O).
In questa condizione, il mozzo (cioè il centro O) si muove con velocità V diretta parallelamente alla strada.
Raggio di rotolamento.
Osservate la figura seguente.
Consideriamo una ruota di raggio R in rotolamento puro, cioè senza che su di essa agisca alcuna coppia motrice o frenante. Il centro della ruota si muove a velocità V e la ruota rotola con velocità angolare ω.
Il raggio di rotolamento è definito come il rapporto tra V e ω. Ossia, R0 = V/ ω.
Per farla breve, e semplice, si può dimostrare che Ro è compreso tra un valore minimo ed uno massimo. Il valore massimo è il valore del raggio della ruota scarica (cioè R); quello minimo, è l’altezza del centro della ruota sul suolo h (che prende il nome di raggio sotto carico).
Insomma, se scrivo quello che ho detto in termini matematici, avrò che h<R0<R.
Quello che m’interessa che comprendiate è che la velocità periferica di ogni punto del battistrada VARIA CICLICAMENTE. Cioè, un qualunque punto del battistrada, se non è a contatto col suolo, dapprima, avrà all’inizio una velocità periferica pari a ωR. Quando però arriva a contatto col suolo, la sua velocità (periferica) rallenta e, partendo da ωR si avvicina sempre più a ωh.

Questo significa che in questa prima fase, cioè dalla condizione indeformata fino ad A, il punto del battistrada STRISCIA e rallenta. Quando arriva in A, però, la velocità non diventa ωh, ma rimane sempre superiore, cioè anche in A continua a strisciare (di poco, ma striscia).
Da A in poi, invece, il punto riaccelera per raggiungere nuovamente la velocità ωR della ruota indeformata. Ovvero, dopo aver lasciato l’orma di contatto assume nuovamente la sua lunghezza iniziale e ritorna la valore iniziale ωR.
Se guardate il grafico che c’è allegato nel disegno, vedete come varia la velocità del singolo punto del battistrada con il rotolamento.
Questo significa che, nel primo tratto (cioè nella fase in cui rallenta passando da ωR per portarsi verso ωh in A) il battistrada si comprime, STRISCIA e rallenta; nel secondo tratto (cioè nella fase in cui riaccelera passando da A per portarsi verso la zona indeformata), il battistrada si estende, STRISCIA e riaccelera. Ma sempre striscia.
Il punto A, quindi, NON è il centro di istantanea rotazione (quello che prima abbiamo chiamato C) della ruota. Il nostro centro di istantanea rotazione, infatti, NON è più sul piano stradale, ma SOTTO il piano della strada! Il mio C sta sotto A!
E tanto più la mia pancia è pronunciata, tanto più in basso andrà C, tanto maggiore sarà lo strisciamento del battistrada in A.
Prima considerazione. Questo è il motivo per cui i pneumatici si consumano: perché strisciano sull’asfalto. Anche se decideste di non fare più curve per il resto dei vostri giorni di guida, consumereste le gomme ugualmente. Ora, è chiaro che il valore di h (cioè del raggio sotto carico) dipende da un sacco di fattori, alcuni dipendenti dal pneumatico (come la struttura della carcassa, dallo stato di usura del pneumatico stesso, etc), altri dipendenti dalle condizioni di impiego (pressione di gonfiaggio, carico, velocità, etc). Per esempio, i pneumatici radiali hanno valori di h minori rispetto ai pneumatici a tele incrociate a pari raggio indeformato R (può sembrare strano, ma è proprio così e dipende dal fatto che il radiale ha una maggiore flessibilità radiale; però hanno valori di Ro meno lontani dal valore di R, cioè il raggio di rotolamento è più prossimo al valore del raggio indeformato).
Però deve essere ben chiaro che, anche se gonfiate tantissimo le gomme, anche se riducete il carico sul pneumatico, comunque, avrete un valore di h inferiore rispetto al valore del raggio di rotolamento e al raggio R indeformato. Cioè, una deformazione ce l’avrete sempre.
Poi, è chiaro che se aumentate il carico o riducete la pressione di gonfiaggio avrete una diminuzione di h e del raggio di rotolamento, mentre vi capiterà il contrario se gonfiate tanto o riducete il carico.
Seconda considerazione: la velocità angolare ω di una ruota dotata di pneumatico è SEMPRE MINORE di una ruota perfettamente rigida (per esempio, che so, di acciaio: un cerchione, tanto per fare un esempio che possiate capire tutti) con pari raggio sotto carico (cioè h, altezza del centro ruota dal suolo) e pari velocità di traslazione (V).
Afferrate bene questo concetto, perché sta alla base di tutto il resto: dalla motricità alla frenatura al funzionamento dell’ABS (lo vedremo!) alla resistenza la rotolamento.
Resistenza al rotolamento.
Abbiamo detto finora che, anche in assenza di coppie frenati o quant’altro, una ruota in condizioni di rotolamento puro offre una resistenza, cioè occorre spendere energia per trascinarla. Gli effetti di questa resistenza si traducono nello spostamento in avanti della risultante Z delle pressioni (che generalmente si indicano con la lettera greca σ, sigma) agenti sull’area di contatto del battistrada col terreno rispetto all’asse della ruota; tanto più avanti quanto più grande è il valore della resistenza al rotolamento.
Come potete vedere dalla figura sottostante, la mia risultante Z è spostata in avanti, (nel senso di moto) rispetto all'asse ruota, della distanza Δx.
Ciò dunque, dà luogo ad un momento resistente pari a Z Δx, dove Δx (che si legge “delta x”) altro non è se non la distanza del punto di applicazione di Z dall’asse della ruota.

La resistenza al rotolamento, quindi, dipende dall’isteresi del pneumatico, cioè dalla impossibilità del pneumatico di restituire TUTTA l’energia che gli diamo per rotolare deformandosi. Ma non basta. Sappiamo anche che, in ogni caso, quando un pneumatico rotola, il battistrada striscia sull’asfalto (e il centro di istantanea rotazione C, che nella ruota rigida indeformata è nel punto di contatto tra ruota e strada, si sposta AL DI SOTTO del piano stradale).
Bene, aggiungiamo che la resistenza di rotolamento è dovuta PER LA MAGGIOR PARTE all’isteresi e solo per una minima parte (meno del 10%, tanto per intenderci) allo strisciamento, alla resistenza aerodinamica e ad altri fattori (tipo l’attrito del mozzo ruota nel centro della ruota).
Ora, guardate sempre bene la figura soprastante.
L’equilibrio alla rotazione mi permette di calcolare la resistenza al rotolamento.
La formula, è questa:
Xr = (-ZΔx + Mf)/h
Mf è il momento di attrito del mozzo ruota. Vale la pena di notare che Mf è NEGATIVO,
cioè nella formula riportata ha il segno positivo dal punto di vista algebrico. ma in realtà è negativo. Quindi la formula diventerebbe:
Xr = (-ZΔx - Mf)/h ossia -(ZΔx + Mf)/h
Ora, solo le ruote folli si trovano in questa situazione come nel disegno illustrato.
Se le ruote sono motrici, infatti, viene applicato un momento motore che deve quantomeno equilibrare i momenti ZΔx e Mf e in più fornire una trazione pari alla somma delle forze Xr, della resistenza aerodinamica e di tutte le altre eventuali dissipazioni di energia. Quindi, in caso di ruota motrice, devo scrivere, invece di Mf, la differenza tra il momento motore applicato (Mm) e il MODULO di Mf. se questa differenza è maggiore di ZΔx, la forza Xr è positiva (perché esercito una trazione, mi muovo e ho resistenza...).
In definitiva, dovete considerare il momento Mf con verso opposto per quello che concerne il nostro ragionamento...e quindi mettere il segno meno (-) nella formula.
La formula: Xr = (-ZΔx + Mf)/h
ha una utilità pratica piuttosto limitata perché è difficile determinare sperimentalmente sia Δx sia Mf.
Ai fini pratici, che sono quelli che c’interessano, la resistenza al rotolamento si esprime con una formula più pratica. Questa:
Xr = - f Z
dove:
- f è il coefficiente di rotolamento ed è molto simile (almeno concettualmente) al coefficiente di attrito; anzi, è un coefficiente di attrito e deve essere misurato sperimentalmente
- Z è la reazione vincolare del terreno alla forza normale. Per noi, e per farla semplice, è la reazione dovuta al peso. Cioè, è il peso che grava sulla ruota. Continuo ad usare Z perché voglio che sia chiaro che è uguale al peso solo in condizioni statiche, in piano. Se siamo su un piano inclinato (in montagna, per esempio) o stiamo accelerando o frenando (dove si devono tenere in considerazione anche i trasferimenti di carico) questo non è più vero.
Il segno meno indica che è una resistenza (quindi, che si oppone al moto): il coefficiente di rotolamento, infatti, per tradizione viene considerato positivo.
Il coefficiente di rotolamento dipende da un gran numero di parametri, quali la velocità di marcia (V), la pressione di gonfiaggio, il carico Z, le dimensioni della ruota, il tipo di fondo stradale, la struttura e il materiale che costituiscono il pneumatico.
Tutte cose, insomma, già scritte in precedenza.
Adesso, alcuni di questi parametri li analizziamo più in dettaglio.
Per esempio, vediamo di analizzare meglio gli effetti della velocità di marcia (V) sul rotolamento: come influenza il rotolamento?
Beh, credo che sia facile da intuire: al crescere della velocità, la resistenza (al rotolamento) aumenta. Però la resistenza NON cresce in modo lineare con la velocità (insomma, con una formula del tipo f = m V), ma in modo NON lineare: dapprima cresce lentamente; poi in misura molto marcata.
La formula che esprime questo andamento è la seguente, ed è molto importante:
f = f0 + k V2
I valori di f0 e di k vanno ricavati caso per caso da prove sperimentali.
Sostituiamo f nella prima formula e avremo:
Xr = (f0 + k V2) Z
Cioè
Xr = f0 Z + k Z V2
Cioè due termini: uno costante e uno funzione della velocità al quadrato.
L’andamento del coefficiente di rotolamento in funzione della velocità è riportato nella figura qui sotto. con due curve: una per un pneumatico radiale; una per un pneumatico convenzionale a tele incrociate.

Si vede che, per entrambi i tipi di pneumatico, il coefficiente ha un andamento lentamente crescente fino ad una certa velocità; poi, si nota un "ginocchio" nella curva (in entrambe le curve: in una più evidente, segno di una minore linearità di comportamento; nell'altra meno evidente, segno di una maggiore progressività di comportamento) oltre il quale il coefficiente di rotolamento subisce un incremento repentino che porta a fargli assumere valori decisamente alti e rapidamente crescenti.
La velocità alla quale la curva presenta un “ginocchio” viene indicato come “velocità critica” del pneumatico.
La presenza della velocità critica del pneumatico è generalmente spiegabile dai fenomeni vibratori che si verificano nel suddetto. In queste condizioni, si manifesta un aumento di resistenza concomitante con il generarsi di vibrazioni che, a partire dalla zona di contatto del pneumatico con la strada, fanno sì che questo si stacchi dal terreno (nella parte posteriore della zona di contatto) e che hanno una lunghezza d’onda pari circa alla lunghezza della zona di contatto con la strada.
Insomma, la velocità critica è quella velocità alla quale i fenomeni vibratori (le vibrazioni) iniziano a manifestarsi e il pneumatico smette di funzionare in modo regolare.
La velocità critica dei pneumatici per auto è compresa tra 100 e 130 Km/h circa (dipende dal tipo di pneumatico e dalle sue caratteristiche, però più o meno cade lì...)
Potete benissimo individuarla anche sulle vostre auto, anche se avete i pneumatici perfettamente bilanciati: c'è una velocità, in quel range menzionato, in cui il pneumatico incomincia a vibrare leggermente, e voi lo sentite benissimo. Superata la velocità critica il pneumatico, poi, si stabilizza (è come la teoria sui rotori, insomma un po' come la lavatrice che vibra di più quando va piano e poi, al crescere della velocità di rotazione si stabilizza): in pratica, il primo modo di vibrare del pneumatico viene superato e le cose si stabilizzano.
Altri parametri che influenzano il coefficiente di rotolamento sono:
Struttura del pneumatico: la natura del materiale con cui sono fatti i pneumatici ha notevole importanza. Per esempio, tra un pneumatico normale, uno da vettura sportiva e una da corsa, quello da corsa avrà un ginocchio ben più in alto e la sua curva sarà ben più “lineare” del pneumatico da vettura normale…
Temperatura di funzionamento: al crescere delle temperatura di funzionamento, diminuisce lo smorzamento del pneumatico; di conseguenza diminuisce la resistenza, che è in gran parte dipendente dall’isteresi del pneumatico. Il pneumatico, insomma, tende ad un equilibrio stabile: un aumento della temperatura fa diminuire l’energia dissipata e quindi la produzione di calore; quando cala la temperatura, l’energia ricresce e quindi anche la produzione di calore, che fa però aumentare la temperatura che a sua volta farà ridecrescere l’energia dissipata, etc etc. si arriva ad una condizione di equilibrio.
Pressione di gonfiaggio: un aumento della pressione di gonfiaggio provoca una diminuzione del coefficiente di rotolamento. E così pure una riduzione del carico sul pneumatico. Il motivo è semplice: riducendo il carico o aumentando la pressione il pneumatico si deforma meno, con tutto quello che ne consegue.
Ecco perché è meglio gonfiare le gomme alla pressione giusta (o anche qualche decimo in più) piuttosto che sgonfiarle…e soprattutto, quando andate in ferie con la macchina carica, GONFIATE LE GOMME!
Dimensioni del pneumatico: i parametri principali sono il raggio del pneumatico (quindi le sue dimensioni) e il rapporto d’aspetto (es: il valore 60 nella misura 195/60 R 14) che indica il rapporto tra larghezza (del battistrada) e “spessore” radiale
Un aumento di entrambi, contemporaneamente, produce una diminuzione del coefficiente di rotolamento ed un aumento della velocità critica.
Ecco dunque una ragione in più per non mettere pneumatici super ribassati sulle vostre auto, che, tra l’altro, sono anche meno confortevoli, più fragili, meno progressivi, etc.
Riguardo al raggio, diciamo che un aumento del raggio ha effetto soprattutto sulla velocità critica, perché a bassa velocità la differenza è minima (ecco perché sulle utilitarie si mettono ruote “piccole” senza problemi).
Anche un aumento del rapporto tra larghezza del battistrada e altezza del pneumatico, a pari rapporto d’aspetto, è favorevole perché porta ad una maggiore rigidezza dei fianchi e quindi una minore dissipazione per isteresi.
Tipo di fondo stradale: diciamo che sul ghiaccio e sul cemento ad agosto, le cose sono un po’ diverse, o no? In prima approssimazione, basta traslare la curva f = f0 + k V2, facendo variare il valore di f0, che equivale a traslare la curva sull’asse delle ordinate (la alzo o l’abbasso, insomma).
Effetto del camber ruota: se la ruota non è dritta, ma ha camber, una parte di quella spinta (momento di autoallineamento, poi vedremo) contribuisce ad aumentare la resistenza al rotolamento e quindi ad aumentare il coefficiente di rotolamento.
Coast down di un veicolo.
Tenete presente la relazione Xr = f0 Z + k Z V2.
Questa è una relazione utilizzabile (a differenza di quella precedente, che era di difficile impiego). Si possono determinare i coefficienti f0 e k dei pneumatici. Ma questi valori interessano solo i costruttori di pneumatici (Michelin, Pirelli & Co).
Chi fa auto è interessato a conoscere, principalmente, altri parametri; ossia, è interessato alla resistenza complessiva (almeno, noi della sperimentazione)…
Ma, implicitamente, “pesa” anche l’effetto della resistenza al rotolamento.
Come?
Semplice: con le prove di coast down. Queste prove (dette sinteticamente “coast down”) sono una delle prove più importanti e più utili tra quelle che vengono fatte, perché permettono di conoscere un sacco di cose. Per esempio:
- sono alla base delle prove di omologazione (quindi, spesso i coast down vengono fatti alla presenza di un funzionario della motorizzazione);
- servono per provare la macchina sul banco a rulli (perché definiscono la curva di resistenza all’avanzamento della vettura);
- permettono di confrontare due vetture e di scoprire eventuali problemi (che so, un problema al cambio che assorbe troppa potenza);
- permette anche di determinare, con buona (direi anche ottima) approssimazione la potenza fornita dal motore;
- consentono di confrontare differenti tipi di pneumatici (e scegliere il migliore dal punto di vista del rotolamento), etc.
Insomma, ripeto: sono prove molto utili. Tanto utili che sono utilizzate da TUTTI i costruttori, TUTTI i produttori di pneumatici, molti fornitori e, persino, molte riviste (almeno, tra quelle che “misurano” le auto).
Tutto nasce dagli americani, negli anni ’40 (se non vado errato).
Come sapete, il limite di velocità, in America, è di circa 50 mph, equivalenti a circa 90 Kmh.
In America, venne “normata” (cioè messa a norma) una prova per la determinazione della resistenza all’avanzamento.
In pratica, gli americani chiamarono “TEMPO di coast down” il tempo impiegato da una vettura (dalla vettura di cui mi interessa conoscere il coast down) il tempo impiegato per passare da circa 95 Km/h a 85 Km/h. In pratica, sono “a cavallo” dei 90 Km/h della velocità limite (da codice). Capite benissimo che, se conosco questo tempo, conosco in pratica la forza media che si oppone al moto a 90 Km/h.
Il perché è semplice e dipende dalla formula F = m a = m ΔV/Δt
Ora:
m è la massa della vettura, che conosco
ΔV è la differenza di velocità, che ho imposto (10 Km/h, cioè 95-85 Km/h)
Δt è il tempo per rallentare di quel ΔV (10 Km/h), che conosco perché l’ho appena misurato.
Quindi, conosco la forza MEDIA che si oppone al moto, a 90 Km/h.
Andando avanti, è chiaro che, se io tendo a far diventare sempre più piccolo quel ΔV, approssimandomi sempre più ad un dv, in pratica, tendo al “limite” di quella formula. Quindi, la mia forza sarà sempre meno MEDIA e sempre più istantanea.
In pratica, riduco sempre più la differenza di velocità e misuro il tempo per passare da V+dV a V e da V a V-dV….
E misuro il tempo, istante per istante.
Se faccio questo non solo “nell’intorno dei 90 Km/h” ma anche alle altre velocità, riesco ad ottenere una curva.
In pratica, oggigiorno, prendo la macchina (naturalmente perfettamente “a posto” sia come angoli, sia come pressione gomme, sia come assetti, sia come tutto il resto…), la lancio a circa 120-130 Km/h e, a quel punto, la faccio rallentare in folle fino a quando non si arresta completamente. Registro la velocità, (a step di 1 Km/h che è l’intervallo ritenuto sufficiente) il tempo, lo spazio percorso e, con pochi, semplici calcoli, ottengo una curva di decelerazione. Rifaccio la prova un numero sufficiente di volte, per avere una corretta precisione statistica, e faccio una interpolazione delle curve così ottenute.
La curva che ottengo è la mia decelerazione “istantanea”, ossia: per qualunque velocità (ovviamente tra 0 e 120 Km/h) conosco la decelerazione a quella velocità….quindi, se moltiplico per la massa dell’auto, ho la curva di resistenza all’avanzamento. Ossia, ad ogni velocità, conosco quanto vale la resistenza all’avanzamento.
Naturalmente, questa curva può essere descritta con una polinomiale…
A noi, basta arrivare ad un polinomio del secondo ordine (la resistenza è proporzionale al quadrato della velocità), ottenendo una relazione del tipo:
F = F0 + F1 V + F2 V2
Ora, per motivi di semplicità, bastano 2 coefficienti, F0 e F2 (F1 lo mettiamo uguale a zero) per avere la nostra curva. Quindi, la formuletta di prima si traduce in:
F = F0 + F2 V2
I due coefficienti F0 e F2 (costante e quadratico) sono quelli che descrivono la mia vettura!
Diamo loro un senso.
Riprendiamo la già nota formuletta della resistenza la rotolamento del pneumatico:
Xr = f0 Z + k Z V2.
Anche qui ho un termine costante e uno quadratico
Quindi, il mio F0 rappresenterà, chiaramente, la parte di rotolamento; l’F2 rappresenta il contributo dovuto alla velocità (al quadrato della velocità): in pratica, il contributo dell’aerodinamica, principalmente.
Certo, dentro al mio F2 ci va anche il termine k Z dell’espressione che si riferisce alla resistenza al rotolamento; ma questo è talmente “piccolo” in peso, rispetto al contributo dovuto all’aerodinamica (in termini matematici si dice che è un infinitesimo di ordine superiore), che lo posso anche trascurare.
Nell’F0, invece, ci cade proprio il mio f0 della resistenza al rotolamento. Ma, nella resistenza al rotolamento, ci va dentro pure – che so - l’attrito dei mozzi ruota (cuscinetti & Co), il contributo dovuto al roll back delle pinze freno, etc. (però, la coppia frenante Mf dovuta al mozzo ruota l’abbiamo già vista ed è stata già oggetto di ampia discussione).
Insomma,
F0 “pesa” il rotolamento
F2 “pesa” l’aerodinamica
Quindi, se sto provando delle gomme e voglio vedere quale delle gomme che sto provando è più scorrevole, quale coefficiente vado a guardare (perché sono sicuro che cambierà)?
Bravi, il mio F0!
Invece, il mio F2, sono certo, cambierà di pochissimo.
Tanto per darvi un’idea dell’ordine di grandezza dei coefficienti qui descritti, vi riporto i valori di F0 e F2 di una vettura qualunque.
F0 = 215 [N]
F2 = 0,0405 [N/(Km/h)2]
Il peso di F2 (cioè dell’aerodinamica) comincia a farsi sentire oltre i 100 Km/h (esattamente come è giusto che sia; ricordatevelo, dunque: l’aerodinamica diventa importante, per la resistenza oltre i 100 Km/h; sotto, conta di più il rotolamento, gli attriti, etc. Questo vale anche per le vostre considerazioni sui consumi di carburante).
Forze scambiate tra ruota e strada.
Fondamentalmente, le forze che la ruota scambia con la strada possono essere suddivise in forze scambiate in senso longitudinale (in pratica, frenata e trazione) e forze scambiate in senso trasversale (le forze che generano la “tenuta di strada”).
Riprendiamo la nostra ruota di prima. Purtroppo non posso riprendere il disegno di prima perché la ruota forma una gobbetta davanti al punto in cui inizia il contatto con la strada che potrebbe trarvi in inganno. Sono quindi costretto a prendere un altro disegno, simile a quello precedente. In pratica qui ho applicato, nel giusto verso, il momento frenante (la coppia frenante) che chiamo Mb. Stavolta, il senso di Mb è quello giusto.
Anche il verso della forza frenante Fb è giusto. Fb è la forza frenante che è applicata nel punto a terra.
La velocità angolare (di rotazione) della ruota, che prima avevamo indicato con ω (omega minuscolo, che in greco si dice omicron), adesso viene indicata con Ω (omega, maiuscolo).
Attenzione bene a questo fatto: gli elementi della fascia di battistrada che entrano in contatto col terreno adesso sono in TENSIONE, mentre prima (nella ruota in rotolamento puro) erano in compressione.
La velocità periferica della ruota (relativa al suo centro O), che nella ruota in rotolamento puro era ωR0 e variava tra R e h, adesso è maggiore. Cioè, il raggio di rotolamento R0, che nella ruota in rotolamento puro era compreso tra h e R, ora si sposta verso R e, al crescere di Fb (cioè della forza frenante) diventa MAGGIORE di R!!!
Di conseguenza il centro di istantanea rotazione C, che nella ruota in rotolamento puro era di poco sotto il piano stradale, si porta ad una maggiore profondità!

Osservate la figura seguente: al crescere della forza frenante, aumenta la profondità di C (da C a C’ nella figura).
Nel caso in cui la ruota, anziché frenata, sia motrice, il centro di istantanea rotazione C, invece, si colloca AL DI SOPRA DEL PIANO STRADALE (da C a C” nella figura).
Questo è molto importante: dove si sposta il centro di istantanea rotazione in caso di frenatura e in caso di trazione.
Ora, in caso di ruota frenata, la velocità angolare della ruota (nella figura di prima indicata con Ω) sarà MINORE della velocità angolare della ruota indeformata di raggio h.
Invece, nel caso di ruota di trazione, la velocità angolare della ruota (nella figura di prima indicata con Ω) sarà MAGGIORE della velocità angolare della ruota indeformata di raggio h.
Adesso, introduciamo il concetto di scorrimento.
Avete presente che cos’è una sgommata? Bene, lo scorrimento è il termine tecnico con cui si “spiega” la sgommata. (spiegandolo con termini alla buona).
Allora, si definisce scorrimento (percentuale), indicato con la lettera greca sigma (σ), della ruota come
σ = (ω/ ωc) – 1 cioè σ = - v/V dove
v è la velocità di spostamento del punto di contatto della ruota con il suolo;
V è la solita velocità del centro O.

Guardando la figura successiva capirete meglio sia la posizione del centro di istantanea rotazione in frenata e in trazione; sia la definizione dello scorrimento percentuale, qui definito come S.
Non fatevi prendere dal panico, le formule sono identiche a quelle di prima…
ωR è la velocità v
e
V è sempre la velocità di O
Il valore di S (o di σ, come volete chiamarlo) è compreso tra 0 e 1 o, se lo mettiamo in termini percentuali, tra 0 e 100 %.
Scorrimento = 0% significa che la ruota è in rotolamento puro
Scorrimento = 100% significa che la velocità del punto C (centro di istantanea rotazione) è uguale a quella del punto O (centro della ruota), cioè che il punto C si trova ALL’INFINITO rispetto al piano stradale, cioè ancora che:
1) Ho le ruote bloccate (in caso di frenata);
2) Sto facendo un “burn out” (senza però muovermi) in caso di trazione.
Rispetto alla condizione iniziale quindi se definiamo C’ il nuovo centro di istantanea rotazione. esso si troverà nei due casi rispettivamente sotto o sopra a C.

La presenza di una velocità di slittamento (la v, che è indicata anche come ωR) NON significa che TUTTA la zona a contatto con la strada stia slittando. Nella prima parte del contatto tra battistrada e suolo, non si ha slittamento. Solo in un (più o meno) limitato tratto di battistrada prima del punto C si ha slittamento, perché la velocità tende a diminuire e quindi si ha lo slittamento. Questa zona tenderà a crescere al crescere del valore di S (detto anche σ). e solo in caso di scorrimento percentuale 100% TUTTA la fascia di battistrada a contatto col terreno sarà in slittamento.
Ora, la forza Fb (forza frenante) è funzione di questo slittamento. ma anche la forza di trazione (che è la stessa cosa, solo vista al contrario).
Per chiarire meglio gli ultimi concetti, proviamo a riassumere così. Osservate la prossima figura.

Convenzionalmente, si parla di rotolamento puro quando alla ruota NON ho applicato alcuna coppia, né motrice né frenante.
In questo caso, fissato un certo carico verticale Z e la velocità V del centro O della ruota, il cerchio ruoterà con una certa velocità angolare pari a ω = V / R0
Il valore di R0 può essere CALCOLATO solo con la formula qui sopra. E basta.
Dove R0 è il raggio della ruota in condizioni di rotolamento puro ed è compreso tra h (altezza da terra del centro ruota O) e R (raggio della ruota inderformata).
Quindi, in condizioni di puro rotolamento, il centro di istantanea rotazione C si trova (leggermente) al di sotto del piano stradale.
Tanto per darvi un’idea, un valore indicativo di dove si trovi C è dato da h/R0 = 0,95, cioè poco sotto il piano stradale… Ricordo che R0 è il raggio (= la distanza) tra C e O…
Se, invece, applico una coppia diversa da 0, cioè se applico una coppia motrice o frenante, questa condizione porta ad una velocità angolare Ω della ruota diversa da ω e quindi ad un riposizionamento del centro di istantanea rotazione da C a C’ che, nel caso specifico di frenata, verrà a trovarsi ad una distanza Rx = V / Ω. Al contrario, in caso di applicazione di una coppia motrice, si riposizionerà AL DI SOPRA del punto C.
In queste condizioni di funzionamento, il punto C della ruota andrà ad avere una VELOCITA’ DI SCORRIMENTO che indichiamo con v. La velocità di scorrimento v varrà:
v = V – Ω R0
A questo punto, sempre nel caso di una coppia frenante, si definisce una grandezza detta scorrimento che, diciamo così, dà l’idea dello “slittamento” di C (e quindi della velocità con cui “striscia”), fatta 100 la velocità del centro ruota O.
Lo scorrimento vale σ = v / V ossia, se metto dentro la formula precedente,
σ = (V – Ω R0) / V = 1 – (ωR0 / Ω R0) cioè 1 - ω / Ω
le stesse relazioni valgono in caso di ruota a cui venga applicata una coppia motrice: semplicemente, si invertirà il segno di σ.
Coefficiente di aderenza.
La forza Fb (riportata in precedenza) che la ruota trasmette al suolo, è funzione dello scorrimento: vale 0 (zero) quando lo scorrimento è nullo (cioè quando la ruota rotola e basta) e cresce in modo piuttosto rapido.
Aggiungiamo anche che cresce fino ad un certo punto, fino a toccare un massimo, e poi diminuisce in modo più o meno pronunciato.
Diciamo che, in prima approssimazione, possiamo ritenere che la forza frenante Fb sia proporzionale, a parità di scorrimento, al carico verticale Z.
Quindi, abbiamo detto DUE cose importantissime:
la forza Fb dipende:
1) dallo scorrimento (percentuale)
2) dal carico verticale sulla ruota.
Si può perciò definire un coefficiente di aderenza (che si chiamerà coefficiente di aderenza longitudinale) μx che vale
μx = Fb / Z

Come vedete dal grafico, la curva del coefficiente di aderenza, funzione dello scorrimento, è praticamente simmetrica rispetto all'origine degli assi.
i valori in cui sigma (σ) è negativo sono le condizioni in cui sulla ruota agiscono momenti frenanti; quelli in cui sigma (σ) è positivo significano che sulla ruota sta agendo una coppia motrice.
In pratica, però, le due curve, quella "negativa" e quella "positiva", sono uguali come andamento.
Allora, per facilitarvi di più le cose, possiamo ragionare solo su una delle due, ricordandoci poi che le stesse considerazioni possono valere anche per l'altro lato della curva.
Per esempio possiamo "segare" via tutto ciò che è negativo e ragionare solo sulla curva che è disegnata nel primo quadrante dove sia σ, sia il coefficiente di aderenza μ sono positivi.
Ecco dunque la curva (unica) su cui andremo a fare i nostri ragionamenti (qualitativi).

Il primo tratto della curva riporta una crescita molto rapida del coefficiente di aderenza; dopodiché si arriva ad un valore massimo e poi, un calo, più o meno repentino, del coefficiente.
I valori di scorrimento percentuale attorno a cui si ottiene il massimo coefficiente di aderenza variano nell'intorno del 15% (valori variabili in funzione di moli parametri, che poi vedremo e, soprattutto, delle caratteristiche del pneumatico; in ogni caso, diciamo che si sta attorno a quel 15%).
Oltre il massimo, la curva ha un ginocchio e poi ridiscende.
Consideriamo, allora, una ruota cui sia applicato un momento frenante. In questo caso, sia μ sia σ sono negativi, ma sulla nostra curva hanno entrambi valori positivi: basta solo che ci si ricordi che siamo in condizioni di frenatura (per il caso di ruota in trazione, varranno le medesime considerazioni).
I tratti di curva compresi tra i valori di coefficiente di aderenza μpt e μst (quelli tratteggiati nella figura; in pratica, dal ginocchio in avanti) sono, nell'uso pratico dell'auto, zone di funzionamento INSTABILE. sono zone di instabilità.
Per capirlo, bisogna prendere l'equazione del moto della ruota. Sarà:
J dω/dt = Fb h – Mb (*)
In pratica, ho fatto l’equilibrio dei momenti.
- J è il momento polare d’inerzia della ruota rispetto ad O (all’asse principale d’inerzia che passa per O);
- ω è come sempre la velocità angolare della ruota;
- Fb e Mb sono, come bene sapete, la forza frenante (applicata nel punto di contatto tra battistrada e ruota) e il momento frenante (dato dalla pinza freni).
(*) Non spaventatevi della formula: in pratica, ho trasformato la F = m a (o, meglio, la F = m dv/dt) per i moti rotatori semplicemente sostituendo alle forze i momenti; alla massa il momento d’inerzia e alla velocità la velocità angolare. Niente di speciale, dunque.
Nel tratto che abbiamo considerato instabile, una diminuzione della velocità ω a velocità V costante, cioè un aumento di σ, porta ad una diminuzione del valore assoluto di Fb (cioè della forza frenante) che è la forza CHE MANTIENE LA RUOTA IN ROTAZIONE (guardate bene la figura)!
Se questa diminuzione di Fb non è accompagnata da una conseguente diminuzione del momento frenante Mb, ne consegue un ulteriore rallentamento della ruota, accompagnato da una ulteriore riduzione di Fb e così via.
Insomma, in un attimo, si arriva la bloccaggio della ruota perché ho un alto valore di Mb ma un basso valore di Fb e questo squilibrio comporta il bloccaggio delle ruota!
In parole più chiare, una volta che ho superato il valore ottimale di σ (il valore massimo), si arriva rapidamente al completo bloccaggio della ruota.
Dico di più: finché mi trovo nel tratto “in salita” della curva, ad ogni aumento di σ ho un aumento del coefficiente di aderenza e quindi posso aumentare anche il mio momento di bloccaggio, cioè posso “pinzare” ancora di più sui freni; quando supero il valore di σ ottimale, mi può succedere ciò che ho detto nel caso in cui non diminuisco il momento frenante Mb.
Ora, non è realistico pensare che un guidatore non professionista sia in grado di dosare la frenatura in questo modo, ossia in modo da impedire che avvenga il bloccaggio, e anche i guidatori professionisti (piloti, collaudatori, etc) devono essere molto attenti. Ecco perché si ricorre ai dispositivi antibloccaggio ABS.
L’ABS, dunque, lavora su questo principio, su questa formula e, tanto per essere più chiari, nella zona di funzionamento del pneumatico indicata nel tratteggio (μpt – μst)
In pratica l'ABS rileva la decelerazione della ruota e, in funzione di questa, attua una riduzione del momento frenante Mb (agendo sulla pressione idraulica dell'impianto per ogni singola ruota) quando la decelerazione supera un valore prefissato. Una volta ripristinata la condizione di funzionamento corretta, col giusto valore di Mb in funzione dello scorrimento percentuale, il funzionamento dell'ABS cessa; ma si possono allora ripresentare le condizioni partenza, col rischio di bloccaggio, che determinano un nuovo intervento dell'ABS e così via. Il risultato è una serie rapida di interventi con una variazione ciclica delle velocità della ruota interessata.
La migliore azione dell’ABS si ha quando il sistema "monitora" TUTTE le ruote singolarmente (mi sembra ovvio: ogni ruota ha condizioni di aderenza e funzionamento differenti dalle altre) e quando le ruote sono "libere" (cioè, ad esse NON vengono applicate coppie che non siano la coppia frenante della pinza freni), quindi prive di coppie motrici. Questo è il motivo per cui su alcuni fuoristrada molto specializzati (es: Mercedes classe G) che prevedono il bloccaggio dei tre differenziali, all'atto del bloccaggio dei differenziali si disinserisce automaticamente l'ABS (se ho i differenziali bloccati, significa che le ruote sono tutte collegate tra loro e ogni azione su una ruota si ripercuote anche sulle altre); oppure, che ai tempi in cui l'Alfa correva nel DTM, la 155 V6 TI "apriva" (letteralmente) i differenziali (ricordo che erano controllati elettronicamente) per migliorare la frenata.
Insomma, per avere i migliori benefici, in vetture dotate di ABS bisognerebbe frenare (con intervento dell'ABS) e schiacciare la frizione (così tutte le ruote sono "libere").
Inoltre la forza frenante (o la trazione) che posso applicare alla ruota è funzione del coefficiente di aderenza (che varia come ben sapete) e della forza normale alla ruota (che, in piano, è il peso) secondo la (nota) formula: Fb = μ Z. Quindi, se ho dei trasferimenti di carico (cosa sono? poi lo vedremo), o comunque delle condizioni che mi facciano variare la forza sulla ruota, questi influiranno sulla frenata o sulla motricità della ruota.
Infine, ricordatevi che il massimo della trazione (e della frenata) avvengono per valori di scorrimento percentuale (σ) intorno al 15% (diciamo tra 13 e 20 %, cos' tanto per tenerci larghi): ciò significa che, per partire veloci occorre sgommare un po' ma non lasciarsi andare a fare delle sgommate eccessive e così pure nel frenare, occorre una leggera sgommatina (modulare la frenata per avere leggeri bloccaggi, corrispondenti al mio 15-20% di scorrimento). Se volete una conferma del lavoro dell'ABS, lanciatevi con la vostra auto a circa 70-90 Km/h e poi fate una bella frenata con intervento dell'ABS. Se avrete avuto l'accortezza di frenare su un fondo regolare e pulito, potrete vedere i segni delle "sgommatine" dovute al ciclare dell'ABS: quelle sgommatine sono, appunto, la dimostrazione tangibile del 15-20% di scorrimento.
Considerazioni.
Come abbiamo detto, e ormai dovremmo aver ben chiaro, l’aderenza (longitudinale) del pneumatico dipende dal peso (guardate che è un errore dire peso, se non siamo in piano; sarebbe meglio dire dalla forza normale al piano del pneumatico) e dal coefficiente di aderenza che ha l’andamento che abbiamo visto nel disegno precedente.
Il coefficiente di aderenza longitudinale dipende a sua volta da differenti parametri, quali il tipo di pneumatico, le condizioni della strada, la velocità, LA FORZA LATERALE (cioè, se c’è un “impegno” del pneumatico in senso trasversale, come quando faccio una curva; cioè ancora se c’è un ANGOLO DI DERIVA: vedremo poi cos’è). Insomma, c’è una forte differenza tra le curve ottenute in differenti casi da differenti sperimentatori (proprio perché sono curve sperimentali: c’è poco di “teorico”, ma questo coefficiente viene rilevato sperimentalmente).
Per esempio, c’è una bella differenza tra pneumatici radiali e pneumatici convenzionali (a tele incrociate), con i radiali che offrono sempre un’aderenza migliore dei convenzionali; e, tra gli stessi radiali, tra i pneumatici tradizionali (detti in gergo “neri”) e quelli, moderni, a basso rotolamento, che fanno consumare poco (detti, in gergo, “verdi”). I neri sono migliori quanto ad aderenza, naturalmente!
Poi, c’è la dipendenza dalla velocità, a sua volta influenzata dalle condizioni ambientali: se vado sull’asciutto, al crescere della velocità vedrò una diminuzione modesta dell’aderenza; se sono sul bagnato, l’aderenza calerà di più (ricordatevelo quando guidate quando piove, significa che, sul bagnato, già tengo meno; sul bagnato, in velocità, tengo PARECCHIO meno!!). C’è l’usura del battistrada che, soprattutto ad alta velocità, ha parecchia influenza. Ma non nel senso che pensate voi: al crescere della velocità, il coefficiente di rotolamento AUMENTA su strada asciutta. Il perché mi sembra chiaro: ridurre l’altezza del battistrada (scolpito, nelle gomme stradali) significa aumentare la superficie dell’area di impronta a terra. Attenzione: ho scritto “su strada asciutta”, perché, invece, su strada bagnata, diminuisce. Soprattutto se lo spessore del velo d’acqua è notevole. In questo caso, infatti, può verificarsi un fenomeno si sostentamento idrodinamico chiamato acquaplaning.
In parole semplici, quando la pressione davanti alla ruota raggiunge il valore di sostentamento idrodinamico (in base alla semplice formuletta della pressione dinamica ½ ρ V2), allora il pneumatico “galleggia” sulla strada. Ora, la pressione di sostentamento idrodinamico dipende, a sua volta, direttamente dalla pressione di gonfiaggio del pneumatico (oltre naturalmente dalla velocità di marcia) e quindi, se voglio ridurre la possibilità di aquaplaning devo gonfiare di più le ruote: sposterò più in alto il punto in cui si manifesta il fenomeno. La cosa è abbastanza intuibile anche in modo più semplice: gonfio di più la ruota e quindi riduco l’area di impronta del pneumatico, quindi avrò carichi per unità di superficie (pressioni) maggiori.
Quindi, quando piove, gonfiare di più le gomme!
Tanto per darvi un’idea, il coefficiente di aderenza , che sul strada asciutta è di circa 1,1-1,15, in caso di aquaplaning può arrivare ad essere anche 0,05. Significa che appena penso di toccare il freno, sono già con le ruote bloccate.
Per impedire il verificarsi della sostentazione idrodinamica, o almeno per ritardarla, bisogna evacuare l’acqua. Si può fare in due modi: o rendo la strada molto permeabile (asfalti drenanti) o scolpisco di più il pneumatico.
Attenzione: gli asfalti drenanti “tengono” molto meno sull’asciutto!
Perché? Perché siccome la “grana” della ghiaia di cui sono composti è maggiore, ci sono più spazi e la superficie di contatto tra battistrada e asfalto appunto si riduce. E, se riduco la superficie.
Bene, nel caso in cui la ruota sia motrice (cioè con coppia motrice) anziché frenata (cioè con momento frenate, come abbiamo discusso fin qui), valgono le stesse, identiche, considerazioni. Semplicemente, tenete presente che il coefficiente di aderenza μ adesso è positivo.
:grazie) alfistavero

