Abbiamo visto i parametri caratteristici delle ruote nelle tre viste: frontale (camber, kingpin inclination, braccio a terra trasversale), laterale (chasse o incidenza laterale del montante, braccio a terra longitudinale) e in pianta (convergenza).
Per ognuna di esse, abbiamo cercato di evidenziare l’influenza di questi parametri sul movimento della ruota (anteriore; ma tutto ciò vale anche per il posteriore a patto di tenere in considerazione che hai un grado di vincolo in più….)
Tutto quello che è stato detto fin qui è INDIPENDENTE dal tipo di sospensione usata, cioè dal tipo di vincolo che “lega” la ruota alla scocca.
Abbiamo visto le differenze tra sospensioni a ruote dipendenti (assale rigido) e quelle a ruote indipendenti (quadrilatero e McPherson). E abbiamo visto che il McPherson è, in pratica, una mezza boiata e viene usato solo perché costa poco perché per il resto, per farlo funzionare bene, occorre un sacco di lavoro di messa a punto che pochi sono in grado (per tempo e per motivi prettamente economici; non certo per know how!!) di fare. La Porsche è una di queste case, per esempio….
Insomma, il risultato di quanto detto finora è questo: il progettista, il tecnico, deve definire il valore assoluto di questi parametri per una certa condizione di assetto del veicolo, che è la condizione NORMALE di marcia, detta di “carico statico”. Ma non basta.
Siccome la ruota è legata alla sospensione, esistono dei vincoli geometrici ben precisi. Vincoli cinematici (o, meglio, elastocinematici: perché vanno considerati anche i silent block che collegano i vari bracci che compongono la sospensione e che si deformano elasticamente sotto l’azione delle forze perturbatrici e, quindi, la cui azione si somma, per così dire, a quella dei bracci stessi..) che obbligano la ruota a descrivere una determinata traiettoria durante i movimenti a cui è costretta quando viene sottoposta alle forze perturbatrici, pur nel rispetto dei 3 (per la ruota anteriore) o 2 (per quella posteriore) gradi di libertà.
Durante questi movimenti, la posizione della ruota rispetto alla scocca varia con CONTINUITA’ e quindi variano con continuità i valori degli angoli e delle quote caratteristiche che abbiamo visto fino ad ora (convergenza, kingpin, campanatura, etc).
Quindi, l’altro elemento che il tecnico deve tenere in considerazione e, soprattutto, sotto controllo è la VARIAZIONE di questi angoli con lo scuotimento. Perché è qui che sta il problema della messa a punto: la macchina, su strada, non sta ferma, e le sospensioni si muovono, sempre!
Poiché questa variazione dipende dal tipo di sospensione e dai suoi parametri geometrici, il discorso si allarga alla impostazione della sospensione. Insomma, almeno a livello teorico (perché poi, nella realtà, si devono tenere in considerazione altri fattori importanti quali ad esempio i costi, i tempi di sviluppo, la necessità di impiegare quanto più possibile parti comuni, etc) il tecnico, dopo aver definito i valori assoluti dei parametri delle ruote, deve scegliere il tipo di sospensione che glieli assicura e dimensionarla in modo tale che le variazioni di tali parametri durante lo scuotimento siano quelle volute.
Ho scritto: a livello teorico, perché comunque vanno tenuti in considerazioni anche fattori che di tecnico hanno ben poco. Va però tenuto presente che, comunque, il tecnico, il progettista, in genere non è un novellino, un pivello; quindi, ha già una certa esperienza che gli consente di “prevedere”, a grandi linee almeno, se la sospensione che gli “impongono” di utilizzare per i più svariati motivi riesca a garantire le prestazioni che si propone di ottenere.
Altrimenti, in fase di impostazione, lo fa presente al responsabile del progetto e, delle due, l’una:
- o si modificano gli obiettivi di prestazione attesi;
- oppure, si decide di “spendere” (tempo, denaro, risorse umane, o quello che volete voi) per centrare gli obiettivi che ci si è posti.
Tanto per essere più chiari: il comportamento cinematico della sospensione può essere rappresentato considerando il sistema ruota + sospensione composto da aste rigide ed accoppiamenti tra le aste e la scocca rigidi; quello elastocinematico, considerando le cedevolezze dei punti di collegamento e dei corpi che costituiscono il sistema (le cedevolezze sono dovute ai tasselli gomma - metallo, i silent block per intenderci, che sono collocati nei punti di collegamento dei bracci delle sospensioni e sugli attacchi alla scocca)
Dati questi due livelli di rappresentazione, le analisi che si possono effettuare sono:
Analisi in scuotimento (per entrambi i comportamenti): si rilevano i carichi verticali (a terra o a centro ruota), le variazioni di convergenza e campanatura per differenti angoli volante, carreggiata e passo, partendo dalla configurazione statica, in funzione dello spostamento (scuotimento) della ruota rispetto alla scocca. Queste grandezze caratteristiche hanno comportamento differente nel caso lo scuotimento sia simmetrico per le due ruote (nel caso di sospensione a ruote indipendenti si considera solo una ruota) o antisimmetrico (lo spostamento di una ruota è di quantità uguale ma in direzione opposta della ruota sull’altro lato. La differenza tra rappresentazione cinematica ed elasto-cinematica, è che in quest’ultimo caso gli elementi della sospensione ed i punti di attacco alla scocca, sottoposti al carico statico passante per l’elemento elastico (boccola), introducono ulteriori cedimenti e quindi variazioni delle grandezze in esame.
Analisi sotto carico (solo per sistema elasto-cinematico, perché non avrebbe senso su quello cinematico, essendo ritenuto perfettamente rigido): il sistema di sospensione è sottoposto a forze e momenti agenti sulla ruota (a terra od a centro ruota), in particolare al carico laterale Fy (forza agente lungo l’asse trasversale), carico longitudinale Fx, (forza agente lungo l’asse longitudinale) e momento autoallineante (momento intorno asse verticale) e vengono misurate le variazioni di convergenza, campanatura, passo e carreggiata.
Guardate questa figura: sono riassunte, in modo schematico, le analisi sopra esposte, per un sistema elasto-cinematico: si vede che nel caso di analisi in scuotimento prevale l’aspetto di geometria su quello elastico, mentre nel caso di analisi sotto carico prevale il comportamento elastico.
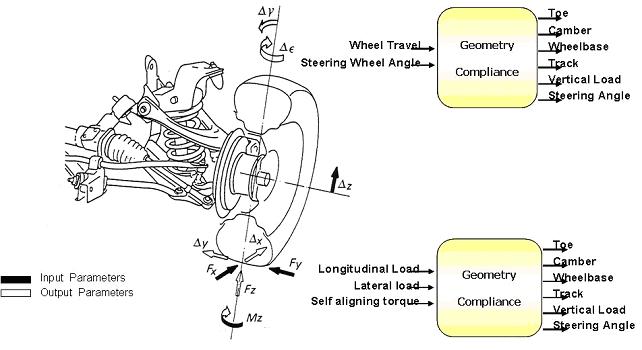
(le frecce più marcate indicano i parametri più influenzati)
La sospensione NON è composta solo di bracci rigidi E BASTA; ma anche di tasselli di gomma (spero che non mi legga qualche vero tecnico che si occupa di sospensioni, sennò sono fregato!!) la cui deformazione DEVE essere tenuta in considerazione.
Introduciamo quindi il concetto di elastocinematica: somma di componente cinematica e di componente di deformazione conseguente al cedimento elastico dei tasselli.
La cedevolezza elastica dipende SOLO dalla forza, non dalla velocità; poi, è chiaro che la forza VARIA nel tempo (non è costante) e quindi è una formula del tipo F = F(t). c'è un transitorio, naturalmente. e c'è una fase di stabilizzazione. ma noi, consideriamo, per ora, la fase regimata.
ma la deformazione dipende dalla forza e basta. la tipica formula della molla D=F/k dove k è la costante elastica e D la deformazione. poi, è chiaro che non è proprio così, perché ci sarebbe da tenere in conto anche la dissipazione di energia, l'isteresi etc. ma per adesso, lo consideriamo perfettamente elastico.
Variazione di convergenza.
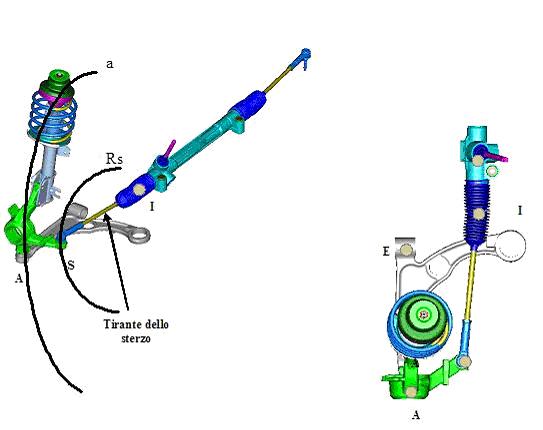
Cominciamo con la grandezza più importante da considerare, quella da tenere maggiormente sotto controllo: la variazione di convergenza. Infatti, è quella che maggiormente incide sulla sovra o sotto sterzatura del veicolo. Dipende da moltissimi parametri, tutti modificabili e oggetto di particolari attenzioni in fase di progetto e messa a punto: dalla geometria della sospensione, dalla posizione della scatola guida, dalla lunghezza dei tiranti dello sterzo. Il perché lo capirete se guardate attentamente il disegno qui sotto. Durante lo scuotimento della ruota, il punto S (lo snodo sulla leva dello sterzo) pensato come appartenente al tirante sterzo descrive un arco di traiettoria Rs di raggio, che dipende dalla geometria della sospensione, differente rispetto al raggio dell’arco a del punto A. Se, durante lo scuotimento, il volante è fisso, comanderà la traiettoria Rs. Quindi, la ruota, libera di ruotare attorno all’asse che passa per A, varierà il proprio angolo di convergenza.
Questo equivale ad avere una sterzatura della ruota indipendente dalla rotazione del volante, ma dipendente dallo scuotimento.
Questo fenomeno prende il nome di roll steer.
Ad esempio, una vettura che ha una geometria della sospensione di questo tipo, che imposta una curva ed in cui la ruota esterna tampona e quella interna rimbalza all’angolo di sterzatura imposto dal guidatore si somma (o si sottrae, dipende dalla posizione iniziale del braccio sterzo) la variazione di convergenza della ruota con lo scuotimento dando luogo a fenomeni di sotto (se sottraggo) o sovra (se sommo) sterzatura.
Il perché mi sembra chiaro, no? Per esempio, imposto la curva con un certo angolo. A causa dello scuotimento della sospensione, la ruota esterna, a tamponamento (cioè che si muove verso la compressione della molla), tende a salire verso l’alto (diciamo così, per intenderci) e trascina il braccetto dello sterzo; il quale, non potendosi allungare, costringe la ruota ad “aprire”, cioè a diminuire l’angolo di sterzo: a far variare la convergenza riducendola. Questo equivale a dare meno angolo volante, cioè la macchina tenderà a sottosterzare. Spero di essermi spiegato.
Lo stesso discorso può essere fatto supponendo che il braccetto sterzo tenda a far chiudere, anziché aprire, la convergenza a tamponamento. In questo caso, l’effetto che otterrò sarà un aumento di angolo sterzo (sterzo più del necessario) e ottengo un effetto di sovrasterzatura.
Come si può porre rimedio a questo fenomeno? Semplicissimo: l’asse della scatola guida deve stare sulla retta passante per il centro di istantanea rotazione della scocca rispetto alla sospensione. In questo modo, l’arco di traiettoria percorso dal punto S dello snodo sterzo sarà uguale, in raggio, rispetto agli archi di traiettoria compiuti dai bracci della sospensione e non avrò alcuna variazione di convergenza. Per fare ciò, devo collocare la scatola guida in un punto ben preciso sul telaietto di meccanica (o sulla scocca). Modificando la posizione (l’altezza, per essere precisi) della scatola guida, modificherò il comportamento della vettura. Così, per esempio, ha fatto l’Audi con la nuova A4, sulla quale la scatola guida, a detta della stessa Audi, è stata spostata per ottenere un comportamento più dinamico….
Naturalmente, alcuni effetti sono voluti intenzionalmente: noi, sulla 147, per esempio, abbiamo volutamente optato per avere una sospensione anteriore che aprisse leggermente (qualche grado) a tamponamento per avere un lieve sottosterzo, comunque assolutamente non fastidioso.
Questo ragionamento vale per le ruote anteriori.
Si può tranquillamente considerarlo valido anche per le ruote posteriori. In questo caso, però, il comportamento si inverte: cioè, se a tamponamento la ruota tende a “chiudere”, oltre ad avere una sensazione di maggiore appoggio, avrò un po’ più di sottosterzo (all’anteriore avrei avuto sovrasterzo); viceversa, se tende ad aprire; ma è una cosa assolutamente da evitare al posteriore (nonostante alcune supercar lo tollerino per avere maggiore agilità).
Il perché è semplice da spiegare: l’aumento o la diminuzione di convergenza in scuotimento comporta un aumento o una diminuzione di angolo di deriva, quindi di capacità di generare forze trasversali, quindi spinte trasversali….poi ci arriveremo…
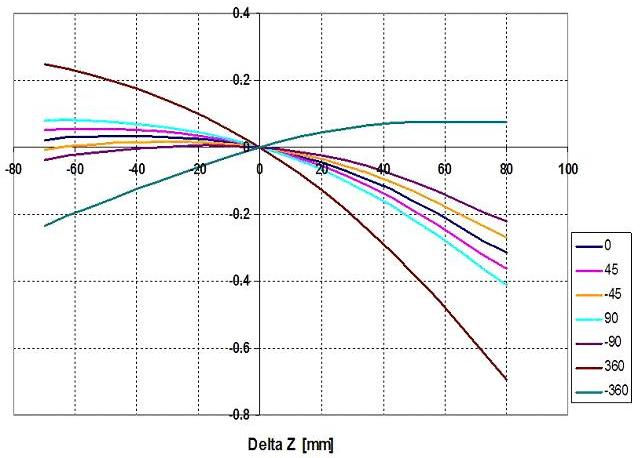
Nella figura che allego sotto, si mostra la caratteristica della variazione di convergenza in funzione dello scuotimento per differenti angoli di sterzata iniziali. E’ un grafico normalmente usato in fase di impostazione vettura per definire le caratteristiche principali e le prestazioni che mi attendo dalla macchina che vado a mettere a punto.
Diamole un’occhiata
Sull’asse delle ascisse trovo lo scuotimento, cioè il movimento verticale della ruota (misurato in millimetri).
Sull’asse delle ordinate, ho la VARIAZIONE della convergenza (e NON la convergenza!!!).
Ho varie curve, ognuna delle quali rappresenta la curva di variazione di convergenza per ogni differente angolo di sterzo: la curva blu è la variazione di convergenza con le ruote diritte (0 gradi sterzo); quella fucsia è la curva corrispondente ad una sterzata di 45 gradi, etc. Insomma, se sto sterzando di –che so- 90 gradi e sto spingendo forte al punto che la macchina sta rollando molto, la ruota esterna alla curva è a tamponamento (si sta schiacciando), per vedere di quanto varia la mia convergenza, dovrò considerare la curva di colore azzurro.
Andiamo avanti: prendiamo, per esempio, la curva corrispondente all’angolo 0 (cioè, sto andando dritto), la curva blu (o nera, boh!). se la guardo, vedo che, se schiaccio la sospensione di 60 mm, la ruota tenderà ad aprire di 0,2 mm. Cioè. Se per esempio, ho impostato una convergenza statica di 2 mm CHIUSA (è un esempio, eh!), se la sospensione si schiaccia di 6 cm la mia convergenza sarà di 1,8 mm!!!!
Il fascio di curve, mi fa subito vedere che, durante la sterzata, la ruota esterna, a tamponamento, (che poi è quella che esprime la forza maggiore, che “guida” per così dire la macchina) tende ad “aprire”, a darmi sottosterzo. Il contrario, se la ruota è in condizioni di rimbalzo (cioè si sta estendendo)
C’è un solo caso in cui la ruota tende a “chiudere”: è quello rappresentato dalla curva verde, che corrisponde a una sterzata di – (meno) 360 gradi: ossia, se giro il volante dall’altra parte (e rimango a tamponamento)! La cosa è logica; seppure difficile da immaginare! Significa far tamponare la ruota in appoggio alla curva, tanto per dare un’idea….
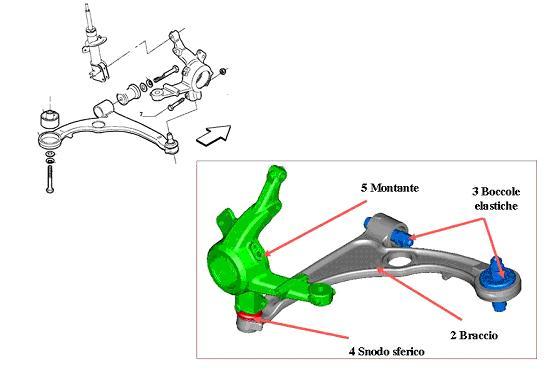
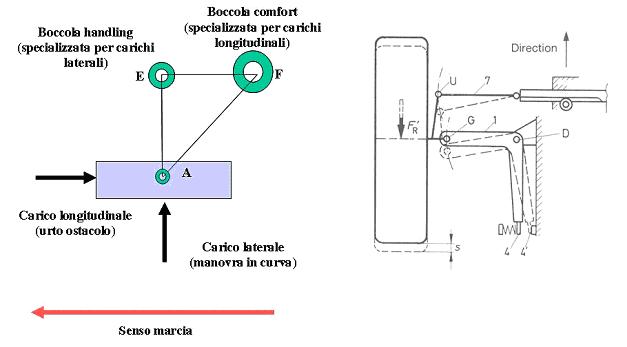
In questa immagine (sotto) potete vedere la posizione delle boccole elastiche (i silent block) che sono responsabili del comportamento elastocinematico (e non solo cinematico) della sospensione.
Una delle due ha solo compiti di garantire l'handling; l'altra, di garantire anche il confort.
Ecco spiegata la specializzazione delle due boccole:
- quella anteriore, che reagisce sotto carichi trasversali, serve per l'handling (appunto);
- quella dietro, che reagisce ai carichi longitudinali (frenata, ostacoli stradali, buche, etc) per il confort.
Abbiamo detto che il roll steer dipende dalle diverse traiettorie a e Rs descritte dallo snodo del braccetto dello sterzo e dalla sospensione. Osservate il disegno qui sotto.
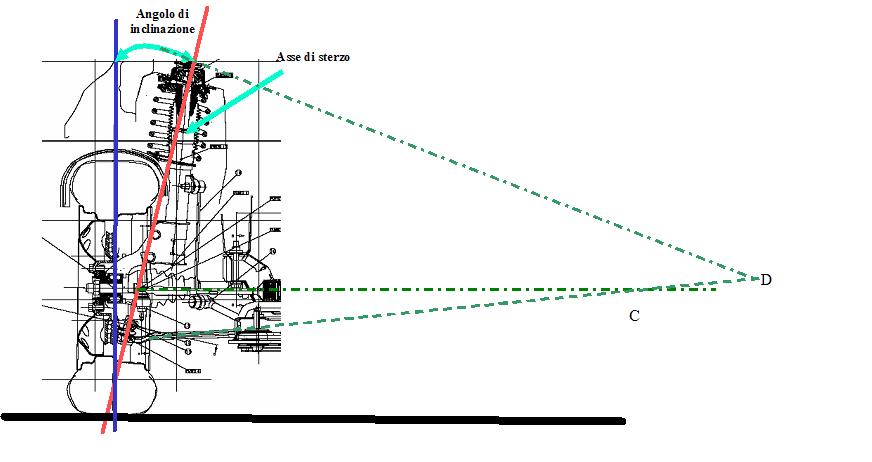
I centri di rotazione C e D delle traiettorie (quelle dei bracci della sospensione e del braccetto dello sterzo) NON coincidono. le traiettorie saranno, dunque differenti e, pertanto, avrò roll steer (ad aprire o chiudere, non importa in questo momento).
Per avere traiettorie coincidenti (quindi nessuna variazione di convergenza, quindi NO roll steer) bisogna che i centri di rotazione C e D delle due traiettorie COINCIDANO.
Ora, per modificare le traiettorie (almeno una tra quelle dei bracci della sospensione e quella dei braccetti dello sterzo), posso agire sulla posizione della scatola guida (alzandola o abbassandola: spostandola, insomma, sposto il certo di rotazione C) oppure modifico l'inclinazione dei bracci della sospensione (così facendo modifico la posizione del centro di rotazione D).
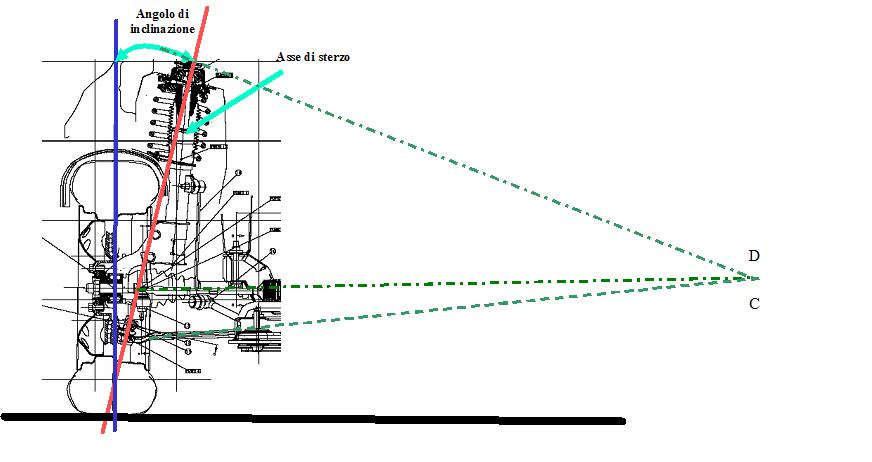
E' quello che ho fatto nella figura qui sopra: ho modificato la posizione della scatola guida (l'ho alzata) e tutto è andato a posto. avrei anche potuto modificare l'inclinazione del braccio inferiore della sospensione; oppure avrei potuto modificare entrambi (braccetto guida e leva inferiore della sospensione).
P.S. non state a esaminare con la lente d'ingrandimento i due disegni: sono uguali, ho solo modificato l'inclinazione delle rette tratteggiate per farvi capire.
Considerazioni sulle variazioni di convergenza in scuotimento.
Come già detto, sono importantissime, perché sono tra le più importanti leve (non le sole, eh) su cui agire per far andare la macchina come si vuole, per "regolare" la tendenza a chiudere o ad aprire di una macchina; ma anche per gestire l'appoggio del posteriore alle medio - basse accelerazioni trasversali; per avere immediatezza di appoggio, per intervenire sulla risposta in due tempi delle vettura, etc.
Infatti, le variazioni di convergenza in scuotimento sono presenti sia all'avantreno, sia al retrotreno.
Diciamo che, in linea di massima, all'avantreno si tende ad avere delle variazioni (dette anche delta convergenza) ad aprire quando la ruota tampona (cioè la sospensione si comprime). Ciò significa far tendere l'auto ad un leggero (leggero, ho scritto eh) sottosterzo, un comportamento verso la stabilità e la sicurezza; questo, in generale, per TUTTE le auto, siano esse TA o TP e anche le sportive. Comunque, diciamo che si lavora sulle variazioni di convergenza per ottenere, nei limiti del possibile, una sterzatura quanto più possibile lineare, senza tendenza a chiudere o ad aprire. Noi, per esempio, lavoriamo moltissimo sulla linearità di sterzatura....
Al posteriore, invece, si tende ad avere variazioni di convergenza a chiudere (naturalmente, no?), cioè ad avere più spinta trasversale: questo porta ad avere una maggiore sensazione di appoggi sicuri e forti anche se, pure in questo caso, ciò determina un leggero sottosterzo. E’ chiaro che una vettura che non comunichi una sensazione di buon appoggio del posteriore non trasmetta un buon feeling, rendendo la guida un po' apprensiva (non riuscire a sentire bene l'appoggio del posteriore è una cosa piuttosto sgradevole quando si va forte, che limita la possibilità di ottenere le massime prestazioni).
Questo, ripeto, in generale. e sia sulle TA, sia sulle TP.
Al posteriore, però, non tutte le case ragionano allo stesso modo...
Per esempio, c'è una casa di auto sportive italiane (di cui non farò il nome) che, su alcune sue auto, fa sì che la sospensione posteriore tenda ad aprire a tamponamento per rendere l'auto molto agile nei cambi di direzione (forse fin troppo se poi qualche supercollaudatore della casa si lamenta perché non riesce a battere il tempo nella Porsche al Nurburgring).
Variazione di campanatura.
Analogamente alle variazioni di convergenza con lo scuotimento della ruota, ci sono le variazioni di campanatura (camber). Pensate al caso più semplice, tanto per farci capire: il ponte rigido. Quando incontro un ostacolo, magari con la ruota destra, la ruota si alza per superarlo e, nell’alzarsi, il camber, che magari in condizioni statiche era 0 (zero), passa ad un valore negativo (perché in pratica il ponte rigido “ruota” piuttosto” che muoversi solamente). Per cui la ruota recupera camber. Ad essere onesti, nel caso del ponte rigido, anche la ruota di sinistra cambia il camber, quando la ruota destra si alza: proprio perché il ponte rigido ruota in caso di scuotimenti asimmetrici (cioè si alza solo la ruota destra, o quella sinistra). Questo è proprio una delle caratteristiche non propriamente positive del ponte rigido.
Nel caso, invece, di scuotimento simmetrico (entrambe le ruote si alzano o si abbassano della stessa quota), allora NON si hanno variazioni di camber. Comunque, spero con questo esempio di avervi fatto capire.
Diciamo che la variazione di camber è legata solo alla geometria della sospensione (e non, come per il caso precedente, anche da altri fattori, come per esempio la scatola guida). Normalmente, è considerata positiva (favorevole) quando la campanatura (il camber) tende a diventare negativa a tamponamento, opponendosi al “ribaltamento” del veicolo.
Poi abbiamo la variazione di carreggiata. Prendiamo, ad esempio, un quadrilatero deformabile semplicissimo.
Durante lo scuotimento, la ruota si muove ma i bracci, ruotando, fanno variare la (semi)carreggiata. Variazione di camber e variazione di carreggiata, soprattutto per le sospensioni indipendenti, sono strettamente legate. Da questo punto di vista, la variazione di carreggiata con lo scuotimento (soprattutto simmetrico; ma pure asimmetrico) dovrebbe essere minimo perché comporta un sensibile strisciamento del pneumatico sul terreno. Inoltre, con lo scuotimento asimmetrico (si alza solo una ruota, come nella marcia in curva), dà luogo a forze che attraverso la ruota si scaricano sulla sospensione e da qui sulla scocca, alterandone le condizioni di equilibrio, con effetti di sovra e sotto sterzatura
Ecco qui due grafici, per darvi un'idea.
il primo è la variazione di camber in funzione dello scuotimento:
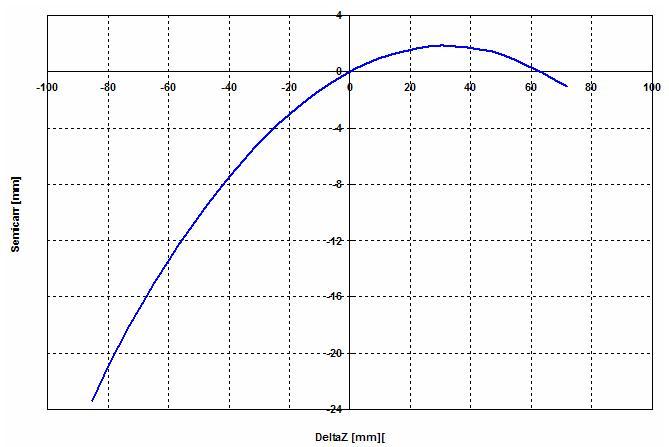
Il secondo è la variazione di SEMIcarreggiata. ho scritto SEMI, quindi...
Vediamo quali sono I parametri su cui agire per intervenire sulle variazioni di camber con lo scuotimento.
Prendiamo le due sospensioni più utilizzate, più “famose”: McPherson e quadrilatero.
Cominciamo col quadrilatero.
Guardate qui:
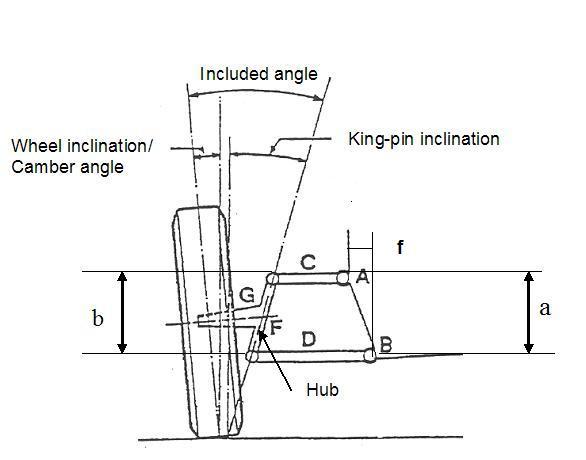
L’ampiezza della variazione è determinata dal rapporto tra le lunghezze delle leve inferiore e superiore (D/C): tanto maggiore sarà tale rapporto, tanto maggiore è l’ampiezza della variazione. Ecco perché le F1 hanno bracci lunghi ma con minime differenze….
La tendenza all’inclinazione, positiva o negativa, viene invece determinata dalle quote a e b (se guardate il disegno, capite che cosa sono). Se a è minore di b la ruota tenderà a ad assumere camber negativo a tamponamento e positivo a rimbalzo. Viceversa se b è maggiore di a.
La quota f invece, una volta fissate le lunghezze dei due bracci C e D, definisce l’inclinazione del montante.
Insomma, come si vede, col quadrilatero posso agire su differenti parametri geometrici per avere le variazioni di camber volute. Insomma, posso controllarle meglio.
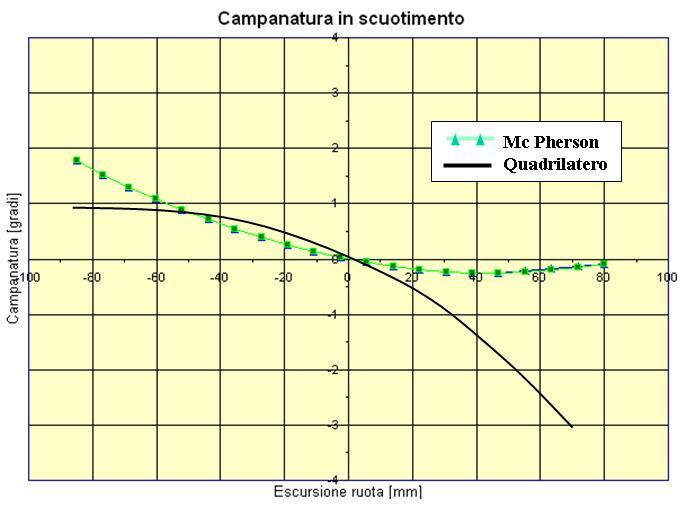
Sul McPherson, invece, rispetto al quadrilatero si perde la possibilità di operare sul braccio oscillante superiore (perché non c’è) mentre sul braccio inferiore si può agire assai limitatamente. Anche da questo punto di vista, il McPherson è più limitativo del quadrilatero e le variazioni di camber in scuotimento sono praticamente un dato di fatto su cui si può agire solo limitatamente.
Questo disegno chiarisce meglio i vantaggi del quadrilatero rispetto al McPherson in termini di variazioni di camber con lo scuotimento:
Ora, tanto per chiarire e completare il discorso, sappiate che finora abbiamo visto le variazioni (di convergenza, di camber, di carreggiata) dal punto di vista prettamente cinematica.
Tenete però presente che le sospensioni sono sottoposte a forze e che, essendo presenti le boccole (silentblock) che a queste forze reagiscono (con cedimenti programmati), come abbiamo visto il loro comportamento è del tipo "elastocinematico"....
Allora anche le forze, applicate dove devono essere applicate sulle ruote, generano deformazioni.
Di seguito allego qualche disegno di variazioni di convergenza, di camber, etc. generate dalle forze in gioco sulla sospensione.
1) Variazione di convergenza in funzione del carico laterale Fy. Guardate come anche la ruota non caricata risenta dell’applicazione della forza: ciò è dovuto all’effetto di interconnessione stabilito dalla linea sterzo.
2) Variazione di campanatura in funzione del carico laterale Fy:
cioè, della forza Fy (forza trasversale: la forza della tenuta di strada, tanto per intenderci. o meglio, quella parte di forza trasversale che compete alla ruota che stiamo guardando, diciamo quella esterna):
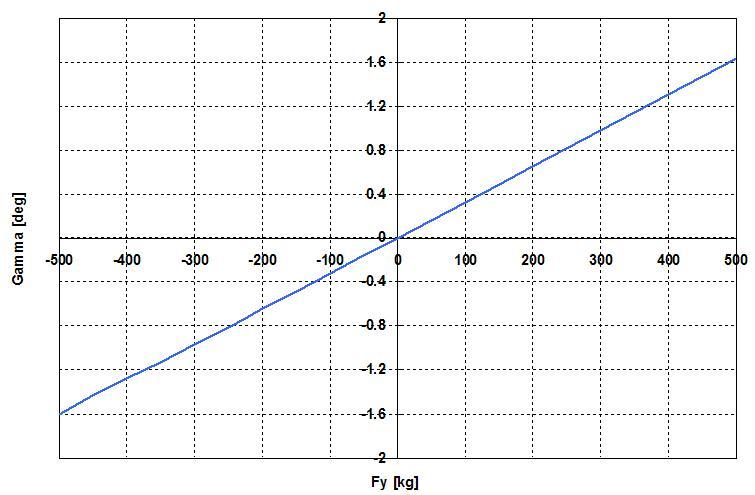
3) Variazione di convergenza in funzione del momento intorno all’asse verticale (momento autoallineante) Mz: anche in questo caso la ruota non caricata risente dell’effetto di interconnessione stabilito dalla linea sterzo.
il momento autoallineante lo descriveremo più avanti.
Il tutto, in sostanza, per dirvi che a determinare le variazioni (di camber, convergenza etc) sono dovute al fatto che si ragiona in termini di elastocinematica (almeno sulle vetture di serie). cioè, i componenti delle sospensioni (bracci, etc) non sono rigidi!
Al di là delle forze e dei momenti auto allineanti, i grafici che ho inserito servono a dimostrare che, almeno per le vetture convenzionali (da strada, per intenderci. e quando dico da strada ci metto pure le Ferrari che, seppure potentissime, sportivissime, sempre da strada sono...), quando parliamo di sospensioni attuali dobbiamo ragionare in termini di elastocinematica.
Ossia, le sospensioni sono composte non solo da elementi, come i bracci (in alluminio, in magnesio o in semplice acciaio), "infinitamente" (non è vero ma noi lo supponiamo) rigidi, che rispondono solo alle leggi della cinematica (cioè si alzano, si abbassano e ruotano: in una parola, si muovono); ma pure da elementi che si "deformano", elementi elastici (le boccole, i silent block) che invece realizzano il movimento solo se sollecitati dalle forze applicate alla sospensione (che si generano durante il movimento dell'auto e le conseguenti reazioni alle ruote) e, in conseguenza di ciò, si deformano consentendo ai bracci ulteriori movimenti.
Tanto per essere più chiaro, per farmi capire: supponiamo, per ipotesi, di stare lavorando alla messa a punto di una vettura che ha una sospensione McPherson.
Per qualche ragione noto che la variazione di convergenza in curva (a tamponamento) non basta per soddisfare la prestazione che voglio ottenere. Ora, per un sacco di motivi NON posso lavorare sulla scatola guida (magari perché ho dei limiti di ingombro che non posso superare; oppure, perché non posso cambiare i bracci perché mi hanno imposto di usare quella guida specifica perché così posso realizzare delle sinergie con un altro modello già esistente; oppure per qualche altro motivo…) e nemmeno posso spostare i punti di attacco della sospensione (sempre per i soliti motivi). Posso allora lavorare sul tassello posteriore (quello che in un disegno postato in precedenza è responsabile dell'handling): ne modifico la rigidezza, per esempio la riduco, e così a pari forza trasversale il tassello si deforma di più, fa ruotare il braccio inferiore di un angolo maggiore e io posso ottenere la variazione di convergenza che mi serve per risolvere il mio problema.
In sostanza, non lavoro solo sulle geometrie della sospensione, ma anche sulle rigidezze delle boccole e dei tasselli, come lavorerò sui pneumatici e sulla taratura di molle e ammortizzatori.
:grazie) alfistavero
Per ognuna di esse, abbiamo cercato di evidenziare l’influenza di questi parametri sul movimento della ruota (anteriore; ma tutto ciò vale anche per il posteriore a patto di tenere in considerazione che hai un grado di vincolo in più….)
Tutto quello che è stato detto fin qui è INDIPENDENTE dal tipo di sospensione usata, cioè dal tipo di vincolo che “lega” la ruota alla scocca.
Abbiamo visto le differenze tra sospensioni a ruote dipendenti (assale rigido) e quelle a ruote indipendenti (quadrilatero e McPherson). E abbiamo visto che il McPherson è, in pratica, una mezza boiata e viene usato solo perché costa poco perché per il resto, per farlo funzionare bene, occorre un sacco di lavoro di messa a punto che pochi sono in grado (per tempo e per motivi prettamente economici; non certo per know how!!) di fare. La Porsche è una di queste case, per esempio….
Insomma, il risultato di quanto detto finora è questo: il progettista, il tecnico, deve definire il valore assoluto di questi parametri per una certa condizione di assetto del veicolo, che è la condizione NORMALE di marcia, detta di “carico statico”. Ma non basta.
Siccome la ruota è legata alla sospensione, esistono dei vincoli geometrici ben precisi. Vincoli cinematici (o, meglio, elastocinematici: perché vanno considerati anche i silent block che collegano i vari bracci che compongono la sospensione e che si deformano elasticamente sotto l’azione delle forze perturbatrici e, quindi, la cui azione si somma, per così dire, a quella dei bracci stessi..) che obbligano la ruota a descrivere una determinata traiettoria durante i movimenti a cui è costretta quando viene sottoposta alle forze perturbatrici, pur nel rispetto dei 3 (per la ruota anteriore) o 2 (per quella posteriore) gradi di libertà.
Durante questi movimenti, la posizione della ruota rispetto alla scocca varia con CONTINUITA’ e quindi variano con continuità i valori degli angoli e delle quote caratteristiche che abbiamo visto fino ad ora (convergenza, kingpin, campanatura, etc).
Quindi, l’altro elemento che il tecnico deve tenere in considerazione e, soprattutto, sotto controllo è la VARIAZIONE di questi angoli con lo scuotimento. Perché è qui che sta il problema della messa a punto: la macchina, su strada, non sta ferma, e le sospensioni si muovono, sempre!
Poiché questa variazione dipende dal tipo di sospensione e dai suoi parametri geometrici, il discorso si allarga alla impostazione della sospensione. Insomma, almeno a livello teorico (perché poi, nella realtà, si devono tenere in considerazione altri fattori importanti quali ad esempio i costi, i tempi di sviluppo, la necessità di impiegare quanto più possibile parti comuni, etc) il tecnico, dopo aver definito i valori assoluti dei parametri delle ruote, deve scegliere il tipo di sospensione che glieli assicura e dimensionarla in modo tale che le variazioni di tali parametri durante lo scuotimento siano quelle volute.
Ho scritto: a livello teorico, perché comunque vanno tenuti in considerazioni anche fattori che di tecnico hanno ben poco. Va però tenuto presente che, comunque, il tecnico, il progettista, in genere non è un novellino, un pivello; quindi, ha già una certa esperienza che gli consente di “prevedere”, a grandi linee almeno, se la sospensione che gli “impongono” di utilizzare per i più svariati motivi riesca a garantire le prestazioni che si propone di ottenere.
Altrimenti, in fase di impostazione, lo fa presente al responsabile del progetto e, delle due, l’una:
- o si modificano gli obiettivi di prestazione attesi;
- oppure, si decide di “spendere” (tempo, denaro, risorse umane, o quello che volete voi) per centrare gli obiettivi che ci si è posti.
Tanto per essere più chiari: il comportamento cinematico della sospensione può essere rappresentato considerando il sistema ruota + sospensione composto da aste rigide ed accoppiamenti tra le aste e la scocca rigidi; quello elastocinematico, considerando le cedevolezze dei punti di collegamento e dei corpi che costituiscono il sistema (le cedevolezze sono dovute ai tasselli gomma - metallo, i silent block per intenderci, che sono collocati nei punti di collegamento dei bracci delle sospensioni e sugli attacchi alla scocca)
Dati questi due livelli di rappresentazione, le analisi che si possono effettuare sono:
Analisi in scuotimento (per entrambi i comportamenti): si rilevano i carichi verticali (a terra o a centro ruota), le variazioni di convergenza e campanatura per differenti angoli volante, carreggiata e passo, partendo dalla configurazione statica, in funzione dello spostamento (scuotimento) della ruota rispetto alla scocca. Queste grandezze caratteristiche hanno comportamento differente nel caso lo scuotimento sia simmetrico per le due ruote (nel caso di sospensione a ruote indipendenti si considera solo una ruota) o antisimmetrico (lo spostamento di una ruota è di quantità uguale ma in direzione opposta della ruota sull’altro lato. La differenza tra rappresentazione cinematica ed elasto-cinematica, è che in quest’ultimo caso gli elementi della sospensione ed i punti di attacco alla scocca, sottoposti al carico statico passante per l’elemento elastico (boccola), introducono ulteriori cedimenti e quindi variazioni delle grandezze in esame.
Analisi sotto carico (solo per sistema elasto-cinematico, perché non avrebbe senso su quello cinematico, essendo ritenuto perfettamente rigido): il sistema di sospensione è sottoposto a forze e momenti agenti sulla ruota (a terra od a centro ruota), in particolare al carico laterale Fy (forza agente lungo l’asse trasversale), carico longitudinale Fx, (forza agente lungo l’asse longitudinale) e momento autoallineante (momento intorno asse verticale) e vengono misurate le variazioni di convergenza, campanatura, passo e carreggiata.
Guardate questa figura: sono riassunte, in modo schematico, le analisi sopra esposte, per un sistema elasto-cinematico: si vede che nel caso di analisi in scuotimento prevale l’aspetto di geometria su quello elastico, mentre nel caso di analisi sotto carico prevale il comportamento elastico.

(le frecce più marcate indicano i parametri più influenzati)
La sospensione NON è composta solo di bracci rigidi E BASTA; ma anche di tasselli di gomma (spero che non mi legga qualche vero tecnico che si occupa di sospensioni, sennò sono fregato!!) la cui deformazione DEVE essere tenuta in considerazione.
Introduciamo quindi il concetto di elastocinematica: somma di componente cinematica e di componente di deformazione conseguente al cedimento elastico dei tasselli.
La cedevolezza elastica dipende SOLO dalla forza, non dalla velocità; poi, è chiaro che la forza VARIA nel tempo (non è costante) e quindi è una formula del tipo F = F(t). c'è un transitorio, naturalmente. e c'è una fase di stabilizzazione. ma noi, consideriamo, per ora, la fase regimata.
ma la deformazione dipende dalla forza e basta. la tipica formula della molla D=F/k dove k è la costante elastica e D la deformazione. poi, è chiaro che non è proprio così, perché ci sarebbe da tenere in conto anche la dissipazione di energia, l'isteresi etc. ma per adesso, lo consideriamo perfettamente elastico.
Variazione di convergenza.
Cominciamo con la grandezza più importante da considerare, quella da tenere maggiormente sotto controllo: la variazione di convergenza. Infatti, è quella che maggiormente incide sulla sovra o sotto sterzatura del veicolo. Dipende da moltissimi parametri, tutti modificabili e oggetto di particolari attenzioni in fase di progetto e messa a punto: dalla geometria della sospensione, dalla posizione della scatola guida, dalla lunghezza dei tiranti dello sterzo. Il perché lo capirete se guardate attentamente il disegno qui sotto. Durante lo scuotimento della ruota, il punto S (lo snodo sulla leva dello sterzo) pensato come appartenente al tirante sterzo descrive un arco di traiettoria Rs di raggio, che dipende dalla geometria della sospensione, differente rispetto al raggio dell’arco a del punto A. Se, durante lo scuotimento, il volante è fisso, comanderà la traiettoria Rs. Quindi, la ruota, libera di ruotare attorno all’asse che passa per A, varierà il proprio angolo di convergenza.
Questo equivale ad avere una sterzatura della ruota indipendente dalla rotazione del volante, ma dipendente dallo scuotimento.
Questo fenomeno prende il nome di roll steer.
Ad esempio, una vettura che ha una geometria della sospensione di questo tipo, che imposta una curva ed in cui la ruota esterna tampona e quella interna rimbalza all’angolo di sterzatura imposto dal guidatore si somma (o si sottrae, dipende dalla posizione iniziale del braccio sterzo) la variazione di convergenza della ruota con lo scuotimento dando luogo a fenomeni di sotto (se sottraggo) o sovra (se sommo) sterzatura.
Il perché mi sembra chiaro, no? Per esempio, imposto la curva con un certo angolo. A causa dello scuotimento della sospensione, la ruota esterna, a tamponamento (cioè che si muove verso la compressione della molla), tende a salire verso l’alto (diciamo così, per intenderci) e trascina il braccetto dello sterzo; il quale, non potendosi allungare, costringe la ruota ad “aprire”, cioè a diminuire l’angolo di sterzo: a far variare la convergenza riducendola. Questo equivale a dare meno angolo volante, cioè la macchina tenderà a sottosterzare. Spero di essermi spiegato.
Lo stesso discorso può essere fatto supponendo che il braccetto sterzo tenda a far chiudere, anziché aprire, la convergenza a tamponamento. In questo caso, l’effetto che otterrò sarà un aumento di angolo sterzo (sterzo più del necessario) e ottengo un effetto di sovrasterzatura.
Come si può porre rimedio a questo fenomeno? Semplicissimo: l’asse della scatola guida deve stare sulla retta passante per il centro di istantanea rotazione della scocca rispetto alla sospensione. In questo modo, l’arco di traiettoria percorso dal punto S dello snodo sterzo sarà uguale, in raggio, rispetto agli archi di traiettoria compiuti dai bracci della sospensione e non avrò alcuna variazione di convergenza. Per fare ciò, devo collocare la scatola guida in un punto ben preciso sul telaietto di meccanica (o sulla scocca). Modificando la posizione (l’altezza, per essere precisi) della scatola guida, modificherò il comportamento della vettura. Così, per esempio, ha fatto l’Audi con la nuova A4, sulla quale la scatola guida, a detta della stessa Audi, è stata spostata per ottenere un comportamento più dinamico….
Naturalmente, alcuni effetti sono voluti intenzionalmente: noi, sulla 147, per esempio, abbiamo volutamente optato per avere una sospensione anteriore che aprisse leggermente (qualche grado) a tamponamento per avere un lieve sottosterzo, comunque assolutamente non fastidioso.
Questo ragionamento vale per le ruote anteriori.
Si può tranquillamente considerarlo valido anche per le ruote posteriori. In questo caso, però, il comportamento si inverte: cioè, se a tamponamento la ruota tende a “chiudere”, oltre ad avere una sensazione di maggiore appoggio, avrò un po’ più di sottosterzo (all’anteriore avrei avuto sovrasterzo); viceversa, se tende ad aprire; ma è una cosa assolutamente da evitare al posteriore (nonostante alcune supercar lo tollerino per avere maggiore agilità).
Il perché è semplice da spiegare: l’aumento o la diminuzione di convergenza in scuotimento comporta un aumento o una diminuzione di angolo di deriva, quindi di capacità di generare forze trasversali, quindi spinte trasversali….poi ci arriveremo…

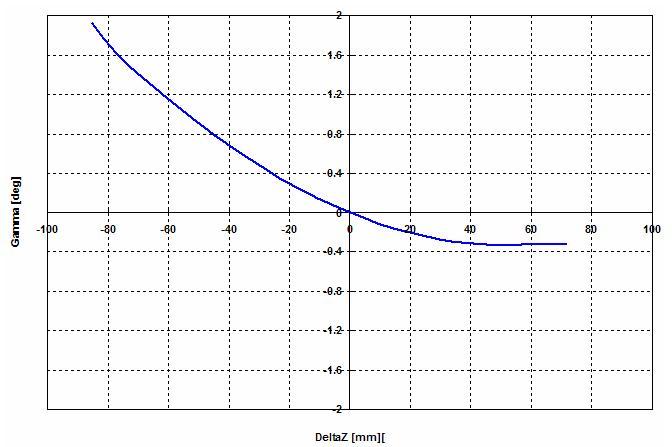
Nella figura che allego sotto, si mostra la caratteristica della variazione di convergenza in funzione dello scuotimento per differenti angoli di sterzata iniziali. E’ un grafico normalmente usato in fase di impostazione vettura per definire le caratteristiche principali e le prestazioni che mi attendo dalla macchina che vado a mettere a punto.
Diamole un’occhiata
Sull’asse delle ascisse trovo lo scuotimento, cioè il movimento verticale della ruota (misurato in millimetri).
Sull’asse delle ordinate, ho la VARIAZIONE della convergenza (e NON la convergenza!!!).
Ho varie curve, ognuna delle quali rappresenta la curva di variazione di convergenza per ogni differente angolo di sterzo: la curva blu è la variazione di convergenza con le ruote diritte (0 gradi sterzo); quella fucsia è la curva corrispondente ad una sterzata di 45 gradi, etc. Insomma, se sto sterzando di –che so- 90 gradi e sto spingendo forte al punto che la macchina sta rollando molto, la ruota esterna alla curva è a tamponamento (si sta schiacciando), per vedere di quanto varia la mia convergenza, dovrò considerare la curva di colore azzurro.
Andiamo avanti: prendiamo, per esempio, la curva corrispondente all’angolo 0 (cioè, sto andando dritto), la curva blu (o nera, boh!). se la guardo, vedo che, se schiaccio la sospensione di 60 mm, la ruota tenderà ad aprire di 0,2 mm. Cioè. Se per esempio, ho impostato una convergenza statica di 2 mm CHIUSA (è un esempio, eh!), se la sospensione si schiaccia di 6 cm la mia convergenza sarà di 1,8 mm!!!!
Il fascio di curve, mi fa subito vedere che, durante la sterzata, la ruota esterna, a tamponamento, (che poi è quella che esprime la forza maggiore, che “guida” per così dire la macchina) tende ad “aprire”, a darmi sottosterzo. Il contrario, se la ruota è in condizioni di rimbalzo (cioè si sta estendendo)
C’è un solo caso in cui la ruota tende a “chiudere”: è quello rappresentato dalla curva verde, che corrisponde a una sterzata di – (meno) 360 gradi: ossia, se giro il volante dall’altra parte (e rimango a tamponamento)! La cosa è logica; seppure difficile da immaginare! Significa far tamponare la ruota in appoggio alla curva, tanto per dare un’idea….

In questa immagine (sotto) potete vedere la posizione delle boccole elastiche (i silent block) che sono responsabili del comportamento elastocinematico (e non solo cinematico) della sospensione.
Una delle due ha solo compiti di garantire l'handling; l'altra, di garantire anche il confort.

Ecco spiegata la specializzazione delle due boccole:
- quella anteriore, che reagisce sotto carichi trasversali, serve per l'handling (appunto);
- quella dietro, che reagisce ai carichi longitudinali (frenata, ostacoli stradali, buche, etc) per il confort.

Abbiamo detto che il roll steer dipende dalle diverse traiettorie a e Rs descritte dallo snodo del braccetto dello sterzo e dalla sospensione. Osservate il disegno qui sotto.

I centri di rotazione C e D delle traiettorie (quelle dei bracci della sospensione e del braccetto dello sterzo) NON coincidono. le traiettorie saranno, dunque differenti e, pertanto, avrò roll steer (ad aprire o chiudere, non importa in questo momento).
Per avere traiettorie coincidenti (quindi nessuna variazione di convergenza, quindi NO roll steer) bisogna che i centri di rotazione C e D delle due traiettorie COINCIDANO.
Ora, per modificare le traiettorie (almeno una tra quelle dei bracci della sospensione e quella dei braccetti dello sterzo), posso agire sulla posizione della scatola guida (alzandola o abbassandola: spostandola, insomma, sposto il certo di rotazione C) oppure modifico l'inclinazione dei bracci della sospensione (così facendo modifico la posizione del centro di rotazione D).

E' quello che ho fatto nella figura qui sopra: ho modificato la posizione della scatola guida (l'ho alzata) e tutto è andato a posto. avrei anche potuto modificare l'inclinazione del braccio inferiore della sospensione; oppure avrei potuto modificare entrambi (braccetto guida e leva inferiore della sospensione).
P.S. non state a esaminare con la lente d'ingrandimento i due disegni: sono uguali, ho solo modificato l'inclinazione delle rette tratteggiate per farvi capire.
Considerazioni sulle variazioni di convergenza in scuotimento.
Come già detto, sono importantissime, perché sono tra le più importanti leve (non le sole, eh) su cui agire per far andare la macchina come si vuole, per "regolare" la tendenza a chiudere o ad aprire di una macchina; ma anche per gestire l'appoggio del posteriore alle medio - basse accelerazioni trasversali; per avere immediatezza di appoggio, per intervenire sulla risposta in due tempi delle vettura, etc.
Infatti, le variazioni di convergenza in scuotimento sono presenti sia all'avantreno, sia al retrotreno.
Diciamo che, in linea di massima, all'avantreno si tende ad avere delle variazioni (dette anche delta convergenza) ad aprire quando la ruota tampona (cioè la sospensione si comprime). Ciò significa far tendere l'auto ad un leggero (leggero, ho scritto eh) sottosterzo, un comportamento verso la stabilità e la sicurezza; questo, in generale, per TUTTE le auto, siano esse TA o TP e anche le sportive. Comunque, diciamo che si lavora sulle variazioni di convergenza per ottenere, nei limiti del possibile, una sterzatura quanto più possibile lineare, senza tendenza a chiudere o ad aprire. Noi, per esempio, lavoriamo moltissimo sulla linearità di sterzatura....
Al posteriore, invece, si tende ad avere variazioni di convergenza a chiudere (naturalmente, no?), cioè ad avere più spinta trasversale: questo porta ad avere una maggiore sensazione di appoggi sicuri e forti anche se, pure in questo caso, ciò determina un leggero sottosterzo. E’ chiaro che una vettura che non comunichi una sensazione di buon appoggio del posteriore non trasmetta un buon feeling, rendendo la guida un po' apprensiva (non riuscire a sentire bene l'appoggio del posteriore è una cosa piuttosto sgradevole quando si va forte, che limita la possibilità di ottenere le massime prestazioni).
Questo, ripeto, in generale. e sia sulle TA, sia sulle TP.
Al posteriore, però, non tutte le case ragionano allo stesso modo...
Per esempio, c'è una casa di auto sportive italiane (di cui non farò il nome) che, su alcune sue auto, fa sì che la sospensione posteriore tenda ad aprire a tamponamento per rendere l'auto molto agile nei cambi di direzione (forse fin troppo se poi qualche supercollaudatore della casa si lamenta perché non riesce a battere il tempo nella Porsche al Nurburgring).
Variazione di campanatura.
Analogamente alle variazioni di convergenza con lo scuotimento della ruota, ci sono le variazioni di campanatura (camber). Pensate al caso più semplice, tanto per farci capire: il ponte rigido. Quando incontro un ostacolo, magari con la ruota destra, la ruota si alza per superarlo e, nell’alzarsi, il camber, che magari in condizioni statiche era 0 (zero), passa ad un valore negativo (perché in pratica il ponte rigido “ruota” piuttosto” che muoversi solamente). Per cui la ruota recupera camber. Ad essere onesti, nel caso del ponte rigido, anche la ruota di sinistra cambia il camber, quando la ruota destra si alza: proprio perché il ponte rigido ruota in caso di scuotimenti asimmetrici (cioè si alza solo la ruota destra, o quella sinistra). Questo è proprio una delle caratteristiche non propriamente positive del ponte rigido.
Nel caso, invece, di scuotimento simmetrico (entrambe le ruote si alzano o si abbassano della stessa quota), allora NON si hanno variazioni di camber. Comunque, spero con questo esempio di avervi fatto capire.
Diciamo che la variazione di camber è legata solo alla geometria della sospensione (e non, come per il caso precedente, anche da altri fattori, come per esempio la scatola guida). Normalmente, è considerata positiva (favorevole) quando la campanatura (il camber) tende a diventare negativa a tamponamento, opponendosi al “ribaltamento” del veicolo.
Poi abbiamo la variazione di carreggiata. Prendiamo, ad esempio, un quadrilatero deformabile semplicissimo.
Durante lo scuotimento, la ruota si muove ma i bracci, ruotando, fanno variare la (semi)carreggiata. Variazione di camber e variazione di carreggiata, soprattutto per le sospensioni indipendenti, sono strettamente legate. Da questo punto di vista, la variazione di carreggiata con lo scuotimento (soprattutto simmetrico; ma pure asimmetrico) dovrebbe essere minimo perché comporta un sensibile strisciamento del pneumatico sul terreno. Inoltre, con lo scuotimento asimmetrico (si alza solo una ruota, come nella marcia in curva), dà luogo a forze che attraverso la ruota si scaricano sulla sospensione e da qui sulla scocca, alterandone le condizioni di equilibrio, con effetti di sovra e sotto sterzatura
Ecco qui due grafici, per darvi un'idea.
il primo è la variazione di camber in funzione dello scuotimento:

Il secondo è la variazione di SEMIcarreggiata. ho scritto SEMI, quindi...

Vediamo quali sono I parametri su cui agire per intervenire sulle variazioni di camber con lo scuotimento.
Prendiamo le due sospensioni più utilizzate, più “famose”: McPherson e quadrilatero.
Cominciamo col quadrilatero.
Guardate qui:

L’ampiezza della variazione è determinata dal rapporto tra le lunghezze delle leve inferiore e superiore (D/C): tanto maggiore sarà tale rapporto, tanto maggiore è l’ampiezza della variazione. Ecco perché le F1 hanno bracci lunghi ma con minime differenze….
La tendenza all’inclinazione, positiva o negativa, viene invece determinata dalle quote a e b (se guardate il disegno, capite che cosa sono). Se a è minore di b la ruota tenderà a ad assumere camber negativo a tamponamento e positivo a rimbalzo. Viceversa se b è maggiore di a.
La quota f invece, una volta fissate le lunghezze dei due bracci C e D, definisce l’inclinazione del montante.
Insomma, come si vede, col quadrilatero posso agire su differenti parametri geometrici per avere le variazioni di camber volute. Insomma, posso controllarle meglio.
Sul McPherson, invece, rispetto al quadrilatero si perde la possibilità di operare sul braccio oscillante superiore (perché non c’è) mentre sul braccio inferiore si può agire assai limitatamente. Anche da questo punto di vista, il McPherson è più limitativo del quadrilatero e le variazioni di camber in scuotimento sono praticamente un dato di fatto su cui si può agire solo limitatamente.
Questo disegno chiarisce meglio i vantaggi del quadrilatero rispetto al McPherson in termini di variazioni di camber con lo scuotimento:

Ora, tanto per chiarire e completare il discorso, sappiate che finora abbiamo visto le variazioni (di convergenza, di camber, di carreggiata) dal punto di vista prettamente cinematica.
Tenete però presente che le sospensioni sono sottoposte a forze e che, essendo presenti le boccole (silentblock) che a queste forze reagiscono (con cedimenti programmati), come abbiamo visto il loro comportamento è del tipo "elastocinematico"....
Allora anche le forze, applicate dove devono essere applicate sulle ruote, generano deformazioni.
Di seguito allego qualche disegno di variazioni di convergenza, di camber, etc. generate dalle forze in gioco sulla sospensione.
1) Variazione di convergenza in funzione del carico laterale Fy. Guardate come anche la ruota non caricata risenta dell’applicazione della forza: ciò è dovuto all’effetto di interconnessione stabilito dalla linea sterzo.

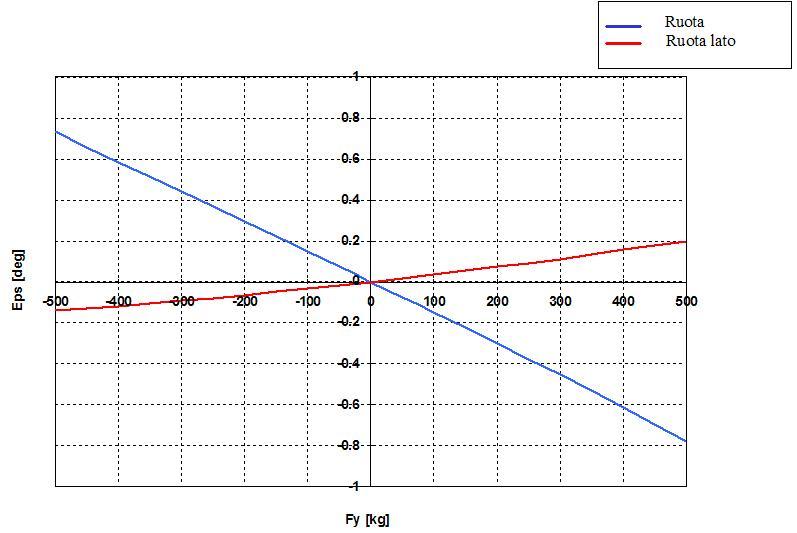
2) Variazione di campanatura in funzione del carico laterale Fy:
cioè, della forza Fy (forza trasversale: la forza della tenuta di strada, tanto per intenderci. o meglio, quella parte di forza trasversale che compete alla ruota che stiamo guardando, diciamo quella esterna):

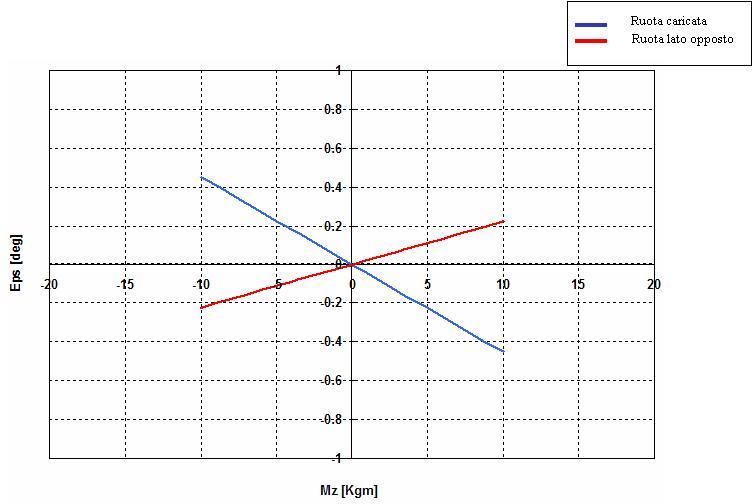
3) Variazione di convergenza in funzione del momento intorno all’asse verticale (momento autoallineante) Mz: anche in questo caso la ruota non caricata risente dell’effetto di interconnessione stabilito dalla linea sterzo.
il momento autoallineante lo descriveremo più avanti.

Il tutto, in sostanza, per dirvi che a determinare le variazioni (di camber, convergenza etc) sono dovute al fatto che si ragiona in termini di elastocinematica (almeno sulle vetture di serie). cioè, i componenti delle sospensioni (bracci, etc) non sono rigidi!
Al di là delle forze e dei momenti auto allineanti, i grafici che ho inserito servono a dimostrare che, almeno per le vetture convenzionali (da strada, per intenderci. e quando dico da strada ci metto pure le Ferrari che, seppure potentissime, sportivissime, sempre da strada sono...), quando parliamo di sospensioni attuali dobbiamo ragionare in termini di elastocinematica.
Ossia, le sospensioni sono composte non solo da elementi, come i bracci (in alluminio, in magnesio o in semplice acciaio), "infinitamente" (non è vero ma noi lo supponiamo) rigidi, che rispondono solo alle leggi della cinematica (cioè si alzano, si abbassano e ruotano: in una parola, si muovono); ma pure da elementi che si "deformano", elementi elastici (le boccole, i silent block) che invece realizzano il movimento solo se sollecitati dalle forze applicate alla sospensione (che si generano durante il movimento dell'auto e le conseguenti reazioni alle ruote) e, in conseguenza di ciò, si deformano consentendo ai bracci ulteriori movimenti.
Tanto per essere più chiaro, per farmi capire: supponiamo, per ipotesi, di stare lavorando alla messa a punto di una vettura che ha una sospensione McPherson.
Per qualche ragione noto che la variazione di convergenza in curva (a tamponamento) non basta per soddisfare la prestazione che voglio ottenere. Ora, per un sacco di motivi NON posso lavorare sulla scatola guida (magari perché ho dei limiti di ingombro che non posso superare; oppure, perché non posso cambiare i bracci perché mi hanno imposto di usare quella guida specifica perché così posso realizzare delle sinergie con un altro modello già esistente; oppure per qualche altro motivo…) e nemmeno posso spostare i punti di attacco della sospensione (sempre per i soliti motivi). Posso allora lavorare sul tassello posteriore (quello che in un disegno postato in precedenza è responsabile dell'handling): ne modifico la rigidezza, per esempio la riduco, e così a pari forza trasversale il tassello si deforma di più, fa ruotare il braccio inferiore di un angolo maggiore e io posso ottenere la variazione di convergenza che mi serve per risolvere il mio problema.
In sostanza, non lavoro solo sulle geometrie della sospensione, ma anche sulle rigidezze delle boccole e dei tasselli, come lavorerò sui pneumatici e sulla taratura di molle e ammortizzatori.
:grazie) alfistavero

