Cosa s'intende per sospensione e quali funzioni svolge?
Per sospensione s'intende quel complesso di elementi che collega la ruota al veicolo, nella maniera più sicura e confortevole per i passeggeri e assicurando alla ruota i gradi di libertà necessari per consentire al veicolo di muoversi.
Cosa sono i gradi di libertà di un corpo e QUANTI sono i g.d.l. di un corpo nello spazio?
I gradi di libertà corpo sono il numero di variabili necessarie per determinare univocamente il suo movimento nello spazio, cioè il numero di coordinate necessario a descrivere il suo moto.
Un corpo nello spazio ha 6 gradi di libertà: 3 traslazioni (secondo gli assi x,y,z) e 3 rotazioni (sempre attorno agli assi x,y,z)
Ogni volta che introduco un grado di vincolo, riduco i gradi di libertà.
Esempio: un corpo su un piano ha 3 g.d.l. Se fisso uno dei punti del corpo, per esempio lo inchiodo, aggiungo 2 gradi di vincolo: può solo ruotare (attorno al punto).
Funzioni svolte dalle sospensioni.
Tenendo conto degli scopi e delle esigenze dell'auto, vediamo di analizzare le funzioni svolte dalle sospensioni.
In primo luogo, poiché la macchina deve potersi muovere e poiché il movimento è assicurato dal rotolamento della ruota, la FUNZIONE PRIMARIA della sospensione è quella di consentire alla ruota di ROTOLARE!!! sarà una banalità, ma questa è la prima cosa: la sospensione deve lasciare alla ruota sicuramente un grado di libertà: la rotazione attorno al proprio asse.
Inoltre, siccome la macchina deve muoversi in ogni direzione, e poiché il cambio di direzione lo si realizza nella maniera più semplice facendo sterzare la ruote (ma non solo), la SECONDA funzione della sospensione è di consentire alla ruota di sterzare!! Cioè, deve lasciare un secondo grado di libertà: la rotazione rispetto ad un asse verticale.
Infine, siccome la macchina si muove sul terreno in ogni direzione, magari in modo confortevole, la TERZA funzione della sospensione è quella di assorbire le asperità della strada, filtrando gli urti e le forze che si generano dal fondo stradale (magari, con qualche elemento che assorbe e dissipa energia; poi vediamo quali...). quindi, deve consentire alla ruota di muoversi in senso verticale, cioè deve lasciare un terzo grado di libertà: il movimento verticale.
Ora, poiché nella macchina le ruote sterzanti sono quelle anteriori, semplificando possiamo dire che la sospensione deve lasciare alla ruota anteriore 3 gradi di libertà; alla ruota posteriore 2 gradi di libertà. in realtà, non è proprio così, se pensate che al posteriore in fase di movimento verticale la ruota è soggetta anche a recuperi di convergenza, quindi a una (seppur minima) sterzatura.
ma per ora, a noi va bene questa schematizzazione di base.
Ora, dal punto di vista FUNZIONALE, quali compiti deve assolvere la sospensione?
La prima è: collegare la ruota alla scocca lasciando i gradi di libertà che servono (alla ruota anteriore e posteriore, cioè 3 e 2).
La seconda: trasformare in energia le asperità incontrate nel movimento sulla strada.
La terza: dissipare, in qualche modo, questa energia.
Per cui, quel complesso di organi (poi vediamo quali) che costituiscono la sospensione può essere formato da elementi diversi come numero, forma disegno etc, e disposti in moltissimi modi. MA DOVRANNO SEMPRE ASSOLVERE AI COMPITI DETTI PRIMA.
Funzionalmente, quindi, gli elementi che costituiscono una sospensione si suddivideranno in:
PORTANTI (che collegano la ruota alla scocca e assicurano i gradi di libertà), per es i bracci oscillanti, i fuselli, gli snodi, tiranti e puntoni
ELASTICI (che collegano elasticamente la ruota, per es. molle, barre di torsione, elementi in gomma come i tamponi)
DISSIPATORI (che dissipano l'energia assorbita dalle asperità, per es. ammortizzatori idraulici.........ma anche le balestre, che sono sia elastiche che dissipatrici.... però, lasciamo perdere. pensate solo agli ammortizzatori.)
Per semplicità, dividiamo le sospensioni in ANTERIORI e POSTERIORI.
Allora, abbiamo visto che ci sono delle funzioni che la sospensione deve svolgere. e il progettista deve, sempre e in ogni caso, progettare delle sospensioni che tengano conto di queste esigenze funzionali (sennò, che cavolo di progettista sarebbe?), e può farlo con grande libertà (almeno teoricamente). Unico vincolo, ripeto ancora perché vi entri in mente, rimane il soddisfacimento delle 3 funzioni principali. però questo non basta, perchè bisogna soddisfarle:
1) nella maniera più affidabile (sennò poi ci troviamo gente che si lamenta ogni volta che salta da un ponte sentendo il gnek gnek del tampone di fine corsa);
2) nella maniera più semplice per la fabbricazione (sennò come farebbe il costruttore a guadagnarci);
3) con il minimo peso (sennò, la gente si lamenta perché la macchina pesa troppo), con il minimo costo (sennò come fanno a darci l'aumento di stipendio?), con il minimo ingombro (sennò facciamo un carro armato, non una macchina);
4) in modo da non penalizzare gli organi a cui ci si attacca (la scocca);
5) offrendo il massimo delle prestazioni tecniche richieste dalla vettura che si sta progettando.
I tipi di sospensione ANTERIORE che si sono salvati a questa serie di VINCOLI (ho fatto apposta ad usare questa parola) importanti e che li soddisfano al meglio, almeno allo stato attuale delle cose, sono 2:
a) sospensione a quadrilatero (e qui ci mettiamo anche il quadrilatero alto della 156/147, perché tecnicamente concettualmente analogo)
b) Mc Pherson
Questo non significa che non possano essere adottati differenti schemi sospensivi per l'avantreno: per esempio, moltissime fuoristrada, di quelle vere hanno un bel ponte rigido, di cui parleremo più avanti- L'Unimog (Mercedes) ha ponti (davanti e dietro) del tipo a U (di cui poi parleremo, dopo il ponte rigido).
Le sospensioni sono suddivise in due grandi classi: a ruote indipendenti e dipendenti.
Le prime sono prive di connessione meccanica tra lato destro e sinistro dell’assale; una forza agente su uno dei lati non ha pertanto effetti sull’altro. Un’altra importante distinzione, all’interno di questa categoria, separa le sospensioni sterzanti da quelle non sterzanti.
Chiaro che il ponte rigido sia una sospensione a ruote dipendenti. le altre che abbiamo descritto, a ruote indipendenti.
Sospensione a quadrilatero
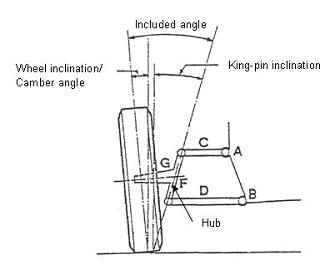
Come si vede la ruota è calettata su un montante (quello che viene descritto con hub) tramite cuscinetti. E qui abbiamo il primo grado di libertà
Il montante, a sua volta, è collegato ai bracci oscillanti (C e D) tramite snodi.
Quindi, il complesso ruota-montante può ruotare attorno ad un asse passante per i due snodi (l'asse di sterzo, tratteggiato e passante per C e D): e qui abbiamo il secondo grado di libertà.
Il complessivo ruota-montante è anche collegato alla scocca tramite attacchi collegati alla scocca stessa (A e B) e quindi può ruotare attorno a quegli attacchi (terzo grado di libertà).
Quelli descritti sono TUTTI organi portanti, mancano gli organi dissipatori e quelli elastici (cioè, rispettivamente, ammortizzatori e molle).
Precisazione: nel disegno del quadrilatero è indicato l'asse di sterzo: vorrei precisare che, affinché sia consentita la sterzata della ruota, i bracci che compongono la sospensione devono convergere (sia quelli superiori, sia quelli inferiori) in un punto; e che la congiungente dei due punti in cui convergono i bracci è appunto l'asse attorno al quale ruota il montante che regge la ruota.
La precisazione potrebbe essere banale, ma non lo è. Infatti, nel caso di sospensione posteriore, i bracci, superiori e inferiori, NON convergono in un punto, ma si dispongono parallelamente (o quasi, poi vedremo come e perché; ma per adesso supponiamo che sia così) gli uni agli altri. in questo caso, NON esiste un asse di sterzo e, infatti, la ruota NON sterza. Oddio, in realtà potrebbe verificarsi il caso che anche al posteriore io possa realizzare una sospensione a quadrilatero utilizzando due TRIANGOLI (uno inferiore e l'altro superiore) che, quindi, realizzano un asse di sterzo. In questo caso, allora, avrò bisogno di un ulteriore braccio che "blocchi" (diciamo così, anche se non è proprio vero; poi anche in questo caso vedremo come si comporta...) la sterzata della ruota posteriore: in questo caso, tale braccio prenderà il nome di "braccio antisterzo" o "finto sterzo".
Sospensione Mc Pherson
Anche qui la ruota è calettata su un montante tramite cuscinetti (primo grado di libertà); Il montante e’ il componente sul quale viene ricavata la sede per alloggiare l’anello esterno del cuscinetto ruota.
Il montante ora è però fissato RIGIDAMENTE all’ammortizzatore.
Alla base del corpo dell’ammortizzatore è saldata una staffa che consente, tramite due bulloni, il collegamento rigido con il montante.
Il complessivo ruota + montante(mozzo) + ammortizzatore può ruotare per l’asse passante per lo snodo sferico (la testina) e per il centro dell’attacco superiore dell’ammortizzatore (secondo g.d.l.): questo è l’asse di sterzo.
Infine, il complessivo di prima può RUOTARE attorno all’attacco sulla scocca (il braccio inferiore è collegato attraverso lo snodo sferico al montante): terzo g.d.l. Quindi, la ruota e’ guidata durante l’escursione verticale dal braccio inferiore (spesso un triangolo, detto triangolo inferiore) che RUOTA (lo ripeto, così si capisce bene) e da un dispositivo a scorrimento lineare di cui e’ parte integrante l’ammortizzatore.
La sospensione Mc Pherson è la più diffusa soprattutto per gli assali anteriori e trova applicazione su (quasi) tutti i veicoli di dimensioni contenute (segmenti A e B). Alcuni costruttori adottano però questa soluzione anche su vetture di segmento superiore, come Porsche, BMW e Jaguar.
Il triangolo inferiore e’ collegato alla scocca o alla traversa di meccanica in due punti, tramite boccole elastiche.
Sul corpo dell’ammortizzatore viene saldato il piattello appoggio molla inferiore. Le spire superiori della molla poggiano su un cuscinetto reggispinta, la cui parte superiore poggia sul tassello duomo. Il tassello e’ il componente di interfaccia dello stelo dell’ammortizzatore e della molla con la scocca. Il collegamento avviene elasticamente al fine di filtrare le vibrazioni.
Differenze tra quadrilatero e Mc Pherson.
Riguardate i 2 disegni, del quadrilatero e del Mc Pherson.
Nel quadrilatero, ogni organo svolge una funzione sola: la molla fa l'elemento elastico; l'ammortizzatore l'elemento dissipatore; i bracci, gli organi portanti e di collegamento.
Però, si può fare in modo che lo stesso organo svolga più funzioni. per esempio, si può sfruttare la grande rigidezza in certe direzioni di una balestra per farle svolgere anche la funzione di organo portante (pensate alla 126)...
sulla strada della semplificazione e della funzione multiruolo dei componenti, si può andare oltre. per esempio, possiamo prendere l'organo dissipatore (cioè l'ammortizzatore) e fargli svolgere funzioni portanti.
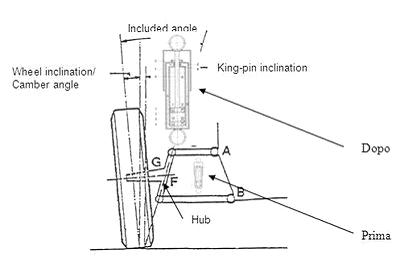
Partendo da una sospensione a quadrilatero si arriva alla McPherson semplicemente sostituendo il montante F, il braccio superiore infulcrato in A e l'ammortizzatore che ho disegnato all'interno e indicato con "prima" con un gruppo montante-ammortizzatore che svolge le funzioni di organo portante e dissipatore assieme.
Prima conseguenza: il McPh è funzionalmente più SEMPLICE del quadrilatero. anzi, si può vedere che con il McPh si può giungere a delle semplificazioni estreme semplicemente sostituendo il braccio inferiore con un organo elastico (e quindi portante) come una balestra (come ho già detto prima: vedete la sospensione anteriore della 126).
Si arriva cioè alla semplificazione estrema, dove non ci sono più organi puramente elastici e puramente dissipatori, ma in cui elementi elastici e dissipatori sono ANCHE portanti.
Vediamo di riassumere quali sono i punti a favore e quelli contro tra quadrilatero e McPh.
1) affidabilità: direi McPh, proprio perché ha meno pezzi (Colin Chapman diceva che tutto quello che non c’è non si può rompere. Io condivido in toto)
2) semplicità: sicuramente, è favorito il McPh, che ha meno elementi del quadrilatero (in pratica, una testa a snodo e il braccio oscillante). Meno pezzi = maggiore semplicità. Anche perché il McPh ha meno punti di collegamento alla scocca. E, soprattutto, li ha disposti in punti più lontani fra loro. Questo significa, poi lo vedremo, minori carichi sulla scocca a pari forze generate dal pneumatico (provenienti dal terreno). Quindi, scocca più leggera. Questo è il motivo per cui Porsche l’ha adottata, sia sulla 911 sia sulle altre (Cayman e compagnia bella).
Ora, questo è sicuramente vero almeno finché si considera il quadrilatero classico. Ma dall’introduzione del quadrilatero “alto” (quello della 147 e 156, per intenderci), che sfrutta gli stessi punti di collegamento alla scocca del McPh, i giochi, sotto questo aspetto, sono praticamente alla pari…
3) spazio disponibile per il vano motore: vince il McPh perché ha eliminato l’ingombro del braccio oscillante (del triangolo, se preferite chiamarlo così) superiore. Infatti, questa soluzione è la preferita dalle vetture a trazione anteriore e motore trasversale: il motore trasversale sottrae molto spazio in trasversale, appunto. E se volessimo fare una macchina col quadrilatero, questa finirebbe per diventare larghissima: quindi, bisogna optare per una sospensione che occupi poco spazio in trasversale. Ecco perché gli scontenti del McPh (cioè Alfa e Honda, adesso vediamo perché scontenti) sono andati verso il quadrilatero alto…
4) costo: forse il motivo principale della grande diffusione del McPh. Fare un McPh costa meno in termini di componenti e di scocca (per il motivo visto prima)…
Sembrerebbe prevalere il McPh, dunque. Però, ci sono anche dei punti a favore del quadrilatero.
1) con il quadrilatero, variando opportunamente la lunghezza e l’inclinazione dei bracci si può ottimizzare meglio che con il McPh la variazione degli angoli caratteristici delle ruote con lo scuotimento: si possono controllare meglio le variazioni di questi angoli. Si può controllare meglio la posizione della ruota nel suo movimento. Ora, siccome il controllo degli angoli caratteristici delle ruote è la condizione PRIMARIA per ottenere il comportamento voluto dell’auto (il miglior handling, ma anche il miglior confort, la migliore stabilità, etc).
2) il McPh presenta, inoltre, un’isteresi maggiore del quadrilatero. Se guardate la figura del McPh, vedete che utilizza, per costruzione, il gruppo stelo ed ammortizzare per guidare il cinematismo della sospensione durante gli scuotimenti verticali della ruota. Questa caratteristica costruttiva comporta che i carichi esterni applicati alla ruota determinano, in funzione dell’architettura della sospensione e del posizionamento della molla, una forza laterale ed un momento applicato sullo stelo.
Le reazioni (vincolari) e le rotazioni dovute all’inflessione dello stelo dell’ammortizzatore in corrispondenza delle guide dell’ammortizzatore determinano l’isteresi del componente, dove per isteresi si intende il valore di forza verticale applicata a terra in grado, vincendo gli attriti, di muovere l’ammortizzatore, a partire da una posizione di equilibrio, che è quella statica con la ruota appoggiata a terra (sotto carico statico, appunto)
Tale grandezza, poiché influenza in modo significativo il comportamento del veicolo su fondi stradali con piccoli asperità, rendendo l’auto meno confortevole e “fluida”, deve essere minimizzata in fase di progetto.
Ecco dunque che, con questi aspetti fin qui enunciati ABBIAMO SPARATO IN FRONTE AL MCPHERSON UCCIDENDOLO ALL’ISTANTE!!
Non sarà mica un caso che il quadrilatero trovi applicazione sulle vetture sportive e sulle berline di lusso, in quanto consente una messa a punto dei parametri elastocinematici, in grado di garantire un ottimo compromesso tra prestazioni comfort ed handling.
Nel quadrilatero, l’ammortizzatore non svolge una funzione strutturale (come nel McPh) di sostegno dei carichi statici ma si limita ad avere compiti dissipativi. Sono pertanto ridotti i fenomeni isteretici, penalizzanti il comfort. Oh, questo anche sulle Ferrari, eh!!
L’unica roba che mi dispiace è anche di aver detto, in pratica, che la Porsche utilizza uno schema di sospensioni economico, non “elegante”, non tecnicamente appagante. Mi dispiace proprio, perché per me l’unico difetto che hanno le Porsche è rappresentato da…I PORSCHISTI!!!
Tra l’altro, questo spiega anche il gran lavoro di messa a punto che la Porsche fa: essendo più difficile il controllo degli angoli col McPh, è più difficile riuscire ad ottenere il comportamento che si vuole da una macchina col McPh….
Quindi la messa a punto del McPh (sempre se si vuole fare un bel lavoro e non ci si accontenta) è decisamente più laboriosa e difficile che col quadrilatero….Chiaro che, se ci si accontenta (diciamo che nessuno che acquista una Daewoo Matiz sta lì a farsi problemi se il recupero di camber in sterzata non consente di avere una linearità di sterzatura da primato….).
Sospensione ad assale rigido
Allora, 3 foto: la prima, quella di un assale rigido (quello della Y10) posteriore; la seconda, di un assale che diventa "ponte" perché garantisce anche trazione ed è anteriore perché ha le ruote sterzanti; il terzo, che preferisco, è quello delle Alfa Nord (serie 116 e derivate, cioè Alfetta & Co.): posteriore e "ponte" (tra l'altro, De Dion)
Le tre foto per dirvi che NON è importante la forma dell'asse, ma COME i bracci lavorano e assolvono al compito che gli è assegnato.
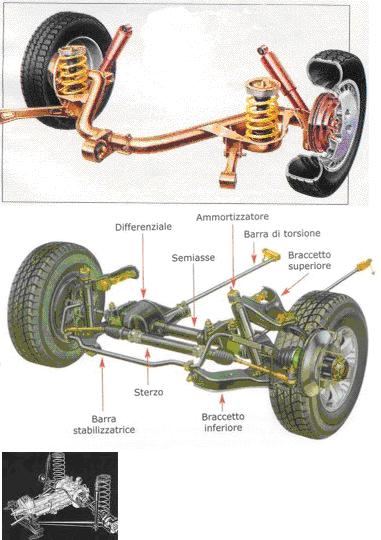
La ruota è fissata direttamente al ponte, attraverso un mozzo e cuscinetti ed è libera di rotolare (primo grado di libertà).
il mozzo, a sua volta, è fissato al ponte in modo rigido nel caso di assale posteriore; oppure, attraverso vincoli rigidi (cuscinetti) che consentono alla ruota di ruotare attorno al proprio asse verticale (secondo grado di libertà, nel caso di sospensione anteriore)
infine, il ponte (tutto) può muoversi in senso verticale (in su o in giù, entro certi limiti): terzo grado di libertà.
Secondo me, e non solo secondo me, il ponte rigido è uno dei più bei sistemi di sospensione perché abbina la semplicità alla facilità di costruzione alla possibilità di mantenere corretti gli angoli delle ruote.
Tra i suoi punti forti ci sono, infatti:
1- semplicità di costruzione
2- leggerezza, soprattutto se, nel caso di configurazione "a ponte", cioè asse con trazione, si separa la parte di trasmissione del moto (differenziale, etc) spostandola dalla parte delle masse sospese: tipico il caso del De Dion Alfa....
3- mantenimento degli angoli delle ruote, soprattutto: mantenimento della perfetta perpendicolarità delle ruote rispetto al terreno
4- mantenimento della scocca distante dal terreno quando si affrontano gli ostacoli
Contro:
1- scarsa escursione della sospensione in caso di supermento degli ostacoli, soprattutto quando si ha una configurazione "a ponte" (il differenziale rompe le balle)
2- variazione concorde della campanatura delle 2 ruote (dx e sx) quando una delle due affronta un ostacolo; questo fa nascere, oltretutto, una coppia giroscopica che si ripercuote sullo sterzo (andatevi a vedere la Faq sui problemi in accelerazione della GTA etc: la spiegazione della reazione giroscopica).
Definizione di massa sospesa e non sospesa
Masse sospese: tutto quello che c'è A MONTE della sospensione
Masse NON sospese: tutto quello che c'è A VALLE della sospensione (cioè ruote, freni, ecc)
La sospensione: metà va nelle masse non sospese; metà nelle masse sospese. Cioè, il braccio lo peso e poi metà del peso lo attribuisco alle masse non sospese e l'altra metà a quelle sospese
Angoli ruote
Siccome abbiamo visto che una delle funzioni della sospensione è quella di collegare la ruota alla scocca e di posizionarla non in modo “qualunque”, ma in un ben determinato modo, per ottenere il comportamento che si vuole, la ruota deve avere angoli precisi CHE VANNO RISPETTATI. Ma perché questi angoli vanno rispettati? Cioè, perché sono così importanti?
Perché se la ruota e i componenti della sospensione non sono posizionati correttamente durante il rotolamento si generano forze non volute le cui risultanti compromettono l'efficacia di assolvimento dei 3 compiti fondamentali della sospensione.
Dunque, guardando la macchina, si nota che l’unico suo collegamento con l’esterno sia la zona di contatto tra il pneumatico e la strada. Ho detto zona e non punto: c’è un motivo, che vedremo dopo.
Adesso, però, supponiamo che sia un punto. Punto di contatto col terreno.
Questo vuol dire che TUTTE le reazioni alle forze messe in gioco dalla macchina o dal conducente come il peso, l’accelerazione, la frenata, le variazioni di traiettoria che fanno nascere forze trasversali, trasferimenti di carico etc, e TUTTE le forze che nascono dagli urti contro gli ostacoli mentre la macchina si sta muovendo sono applicate al PUNTO A TERRA della ruota.
Ora, se leghiamo queste forze ai 2 o 3 (nel nostro caso, visto che parliamo di sospensione anteriore, diciamo 3) gradi di libertà della ruota, tiriamo la conclusione che il punto a terra deve essere tale, cioè messo in posizione tale, da ridurre al minimo le perturbazioni (le reazioni) che tali forze possono provocare sul comportamento dell’auto e gli sforzi che il guidatore deve compiere.
Il punto a terra deve avere quindi una posizione ben definita rispetto agli assi di rotazione della ruota (e agli spostamenti) e questo lo si ottiene dando determinati ANGOLI di impostazione sia alle RUOTE, sia ai suoi ASSI DI ROTAZIONE.
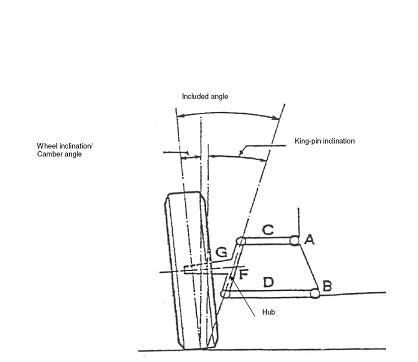
Guardiamo prima i parametri caratteristici che si vedono nella VISTA FRONTALE (e che sono STRETTAMENTE collegati tra loro):
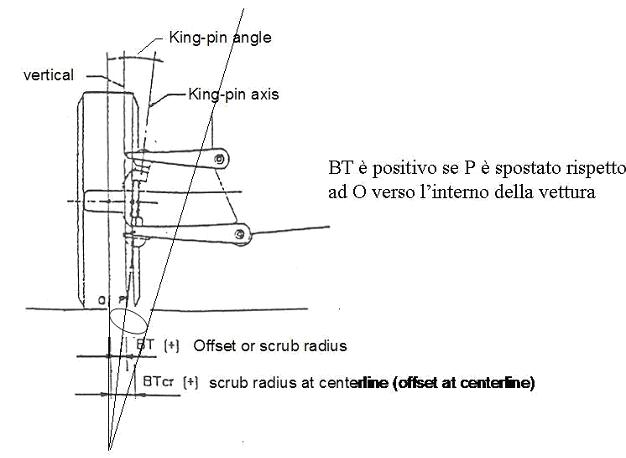
- Camber (o Campanatura): è l’angolo tra la verticale e l’asse passante per la mezzeria della ruota. Positivo quando, come nella figura, la ruota diverge in alto. Negativo, al contrario. Chiaro che si misura in gradi!!!!!
- Inclinazione TRASVERSALE del montante (o King Pin): è l’angolo formato tra la verticale e l’asse di sterzo (cioè la congiungente i due snodi -superiore e inferiore- della sospensione). Anche questo si misura in gradi!!!
Ecco perché, prima, ho scritto PUNTO di contatto a terra tra pneumatico e strada: vedete che prendo sempre la MEZZERIA della ruota? E se suppongo la ruota rotonda (meglio: circolare) e perfettamente rigida, la circonferenza (cioè la mezzeria della ruota) non tocca forse la strada in un punto? In realtà, il contatto tra strada e ruota è una superficie, non un punto (poi lo vedremo). E la ruota NON è indeformabile (anche questo lo vedremo poi).
Guardate questo secondo disegno:
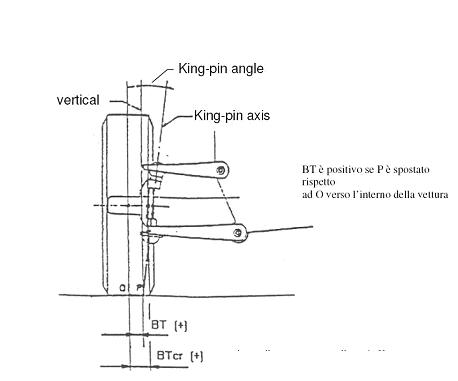
- Braccio a terra trasversale: è la distanza tra il punto a terra della ruota (O in figura) e l’intersezione tra il piano stradale e l’asse di sterzo (il punto P)
Guardateveli bene, questi parametri; perché sono collegati tra loro e, agendo su di essi, si cerca di ottenere sempre il medesimo scopo: RIDURRE l’influenza delle forze verticali (peso, soprattutto; ma anche trasferimenti di carico, deportanza aerodinamica etc) e delle forze longitudinali (frenata e, se stiamo parlando di vetture a trazione anteriore, accelerazione, perché stiamo considerando ruote anteriori; ma le stesse considerazioni valgono se consideriamo ruote posteriori, ovviamente NON sterzanti ma per le quali valgono le stesse, identiche, medesime regole, compreso l’asse di sterzo!!! Ma pure forze perturbatrici conseguenti agli urti contro gli ostacoli) sul comportamento del veicolo.
Il braccio a terra trasversale è BT cioè il segmento O-P
Vediamo allora quali effetti hanno queste grandezze sulle forze che agiscono in marcia (e poi, anche da fermo).
In marcia, dunque, si possono avere forze longitudinali dovute a frenatura e effetti perturbanti dovuti a urti della ruota contro il terreno, forze di resistenza al rotolamento generate dai pneumatici stessi, ect. HO VOLUTAMENTE TRALASCIATO LE FORZE DOVUTE ALLA TRAZIONE! Perché, semplice: lo vedrete tra poco.
Comunque, TUTTE queste forze vengono applicate al punto di contatto tra ruota e terreno. Sono forze che tendono a far oscillare la ruota attorno al suo asse di rotazione.
Osservate la figura:
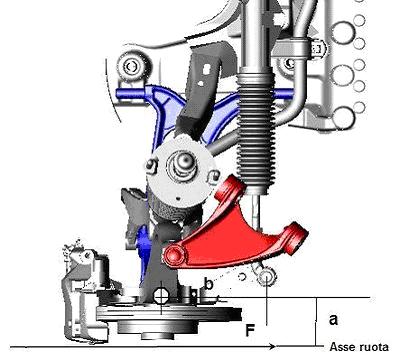
E’ la sospensione anteriore della 147, vista dall’alto. Il pallino bianco è l’impronta del punto di contatto (a terra) dell’asse di sterzo col terreno. F è la forza longitudinale che, come detto, è applicata al punto di contatto tra ruota e terreno (lungo l’asse della ruota).
Quello indicato con a è il braccio della forza rispetto al punto a terra (è il braccio a terra trasversale, quello che nel disegno della settimana scorsa come BT. Allora, alla ruota viene applicato un momento M= F a.
Ora, se le forze applicate sulla ruota destra e sulla sinistra agissero contemporaneamente (e fossero uguali), il conducente non avvertirebbe nessuno sforzo al volante. In realtà, generalmente, avviene che le forze sono diverse: sia perché, magari, la forza F compare solo su una delle due ruote (per esempio, quando affronto un ostacolo); sia perché la forza F dipende da un sacco di fattori, come il peso, l’aderenza locale, l’equilibrio dei freni, etc..
Quindi, quasi sempre, la realtà ci dice che sulla ruota destra e su quella sinistra agiscono forze di intensità differente. In questo caso, quello reale, avviene che il momento M si ripercuote sulla tiranteria dello sterzo, distante b dal centro di rotazione (che è il nostro punto di contatto col terreno che determina il braccio a terra) della ruota, generando una forza S = M / b cioè F a/b.
Questa forza S tenderà a far ruotare il volante in una determinata direzione. Nel nostro caso, verso sinistra; se invece il braccio a terra fosse negativo, cioè il punto cadesse all’esterno dell’asse ruota, la forza S avrebbe segno contrario e il volante tenderebbe a ruotare a destra. Insomma, col braccio a terra positivo la ruota tende ad aprire in frenata; col braccio a terra negativo la ruota tende a chiudere in frenata e quindi si tende a mantenere la traiettoria, diciamo così…questo è uno dei motivi, per esempio, per cui le macchine dotate di ABS hanno generalmente braccia a terra negativi….
Torniamo alla forza S. Il conducente sarà allora costretto a controbilanciare questa sterzata (che, ricordiamolo, è IMPROVVISA!) con un momento applicato al volante e, nel caso di forze dovute al contatto con ostacoli improvvisi o grandi valori di braccio a terra è estremamente difficile da controllare, perché appunto improvvisa ed elevata.
Un modo per ovviare a tale inconveniente è quello di ridurre la forza S: quindi, si può agire aumentando b (difficile da fare perché ciò significa agire sul cinematismo dello sterzo e questo comporta tutta una serie di altre conseguenze pesanti); oppure, visto che non si può ridurre F, allora si riduce il braccio a terra (a). Ma col McPh è difficile, perché per motivi di spazio (dove metto la molla che è grossa?) il McPh ha sempre una certa inclinazione del montante (king pin). Per ridurlo davvero, devo cambiare sospensione: passo allora al quadrilatero alto: in pratica, sposto il braccio superiore, come ho già detto la settimana scorsa, da dentro la ruota a SOPRA la ruota e sfrutto gli stessi attacchi alla scocca del McPh….
Prima, ho detto: consideriamo solo le forze resistenti, dovute a frenatura, etc.
Bene, tenete ben presente questo: LE FORZE FRENANTI (frenatura, resistenza per attrito, perturbanti, etc) VENGONO APPLICATE NEL PUNTO A TERRA (punto di contatto tra ruota e terreno). INVECE, LE FORZE MOTRICI VENGONO APPLICATE AL CENTRO DELLA RUOTA. Allora, se vogliamo applicare la stessa teoria in caso di forze di trazione, dovremo applicare la nostra forza F al centro della ruota (e nel disegno della sospensione vista dall’alto non cambia nulla a livello di F) e usare, anziché il braccio a terra (la distanza a del disegno qui sopra), il BRACCIO A CENTRO RUOTA
Guardate la foto di settimana scorsa (pagina 8), quando abbiamo discusso sul significato del punto indicato come BTcr… Bene, ADESSO VE LO POSSO SVELARE: è il BRACCIO A CENTRO RUOTA. Anche il braccio a centro ruota deve essere ridotto; SOPRATTUTTO il braccio a centro ruota deve essere minimizzato, perché le coppie (le forze) motrici sono elevate e quindi è più evidente il problema. Bene : questo è il torque steer, (di cui abbiamo parlato nella Faq della 147 GTA).
Dicevamo che ci sono dei modi per ridurre questo braccio a terra. Abbiamo visto, per esempio, che possiamo cambiare sospensione (quadrilatero alto invece di McPh); ma si può anche AUMENTARE IL KING PIN (cioè inclinare di più il montante), oppure inclinare di più la ruota dando campanatura (camber) positiva.
Vediamo. Partiamo da quest’ultima proposta: vi ricordate la Fiat Regata, o la Ritmo? Non avevano forse le ruote davanti con camber positivo? Yes, lo avevano fatto per questo motivo. Peccato però che per ovviare ad un problema se ne era generato un altro: l’usura dei pneumatici, che si consumavano tanto nel bordo che era in contatto col terreno. Chi aha avuto la Regata, mi sa dire quanti treni di gomme anteriori ha cambiato?
In realtà la regata aveva anche il king pin elevato….sennò avrebbe consumato le ruote ancora di più.
Vediamo allora cosa significa aumentare il kingpin.
L’inclinazione del montante genera quel problema di cui si parlava nel 3d della 147 GTA: se ho un kingpin elevato, ho pure in questo caso del torque steer.
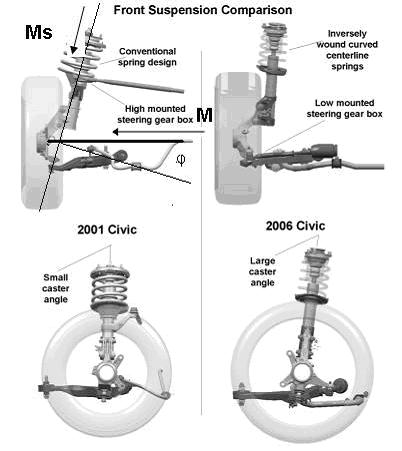
L’asse di sterzo tende ad autosterzare se forma un angolo α diverso da 0 con il semialbero (il semiasse) che porta il moto.
Il momento di sterzatura vale Ms = M (BTcr/R + sinφ) dove BTcr è il braccio a centro ruota (dovreste saperlo benissimo, adesso) e R è il raggio di rotolamento della ruota.
Ora, tralasciando il termine BTcr/R, si può scrivere che Ms = M sinφ.
Tanto più è inclinato il montante, tanto maggiore sarà il momento autosterzante (vedi 164 3.0)…Quindi, bisogna raddrizzare ‘sto montante. Ma col McPh è impossibile averlo perfettamente dritto (come con il quadrilatero)….
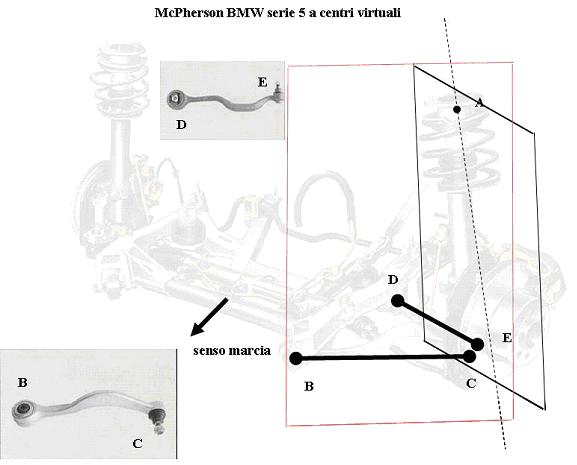
In realtà, c’è un ulteriore modo di ridurre i bracci a terra (e a centro ruota) col McPh: fare in modo che l’asse di sterzo stia il più vicino possibile all’asse di mezzeria della ruota facendo in modo che il vertice che collega i due bracci che compongono il triangolo inferiore, per esempio, cada “al di là” della ruota. Per fare ciò, bisogna che il triangolo della sospensione NON sia un triangolo fisico, cioè non sia un pezzo unico reale; ma sia composto da due bracci che, opportunamente inclinati, vadano ad incontrarsi in un punto ben determinato che NON è fisico ma VIRTUALE (cioè, lo determini sul foglio da disegno, ma non nella realtà). Un classico esempio è la sospensione ad asse di sterzo semivirtuale (semi perchè il punto sul duomo è reale che più reale non si può) della BMW (es serie 5): beccatevi ‘sta sospensione, curatissima…
Finora abbiamo visto cosa succede se la macchina si sta muovendo.
Vediamo ora che influenza hanno i parametri che abbiamo visti (kingpin, camber e bracci a terra vari) a vettura ferma.
A vettura ferma prevalgono le forze dovute alla resistenza offerta dal pneumatico alla rotazione intorno al suo asse.
Rammento che l’asse di sterzo non è altro che l’asse attorno cui ruota la ruota (scusate il gioco di parole)….
Se ho braccio a terra, tutto il momento M = F a di prima me lo ritrovo nello sforzo che devo applicare al volante.
Se la sospensione non avesse braccio a terra (se cioè fosse nullo il valore del braccio a terra) il punto di intersezione dell’asse di sterzo della sospensione coinciderebbe con il punto a terra di contatto della ruota. Quindi, per sterzare da fermo (o a bassa velocità) la ruota dovrebbe strisciare sul terreno, richiedendo una certa fatica fisica (anche se comunque minore rispetto a prima)
Insomma, comunque la giro, sono fregato!!
Però, il kingpin e la campanatura possono essermi un po’ d’aiuto.
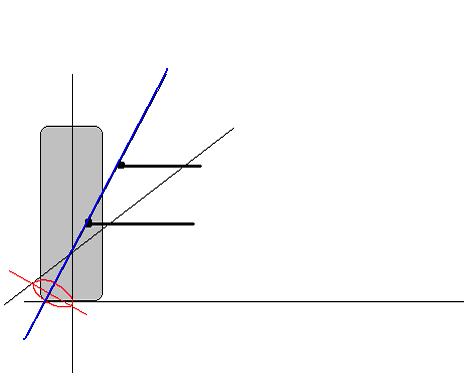
Guardate questa figura: ho prolungato l’asse del camber e quello di sterzo che, in questo caso, si incontrano al di sotto del terreno.
La ruota, tanto per essere chiari, durante la sterzata descrive un cono avente per asse l’asse di rotazione. Esaminando il punto di contatto col terreno, si vede che, a partire dalla posizione di marcia rettilinea dove il contatto avviene sulla superficie stradale, durante la sterzata questo tenderebbe a seguire l’ellisse che ho disegnato: in pratica, il punto di contatto a terra della ruota tenderebbe ad andare SOTTO la linea di terra. Ora, questo NON è chiaramente possibile. Il punto costringe allora la scocca ad ALZARSI vincendone il peso. Parte dell’energia spesa dal conducente per sterzare va appunto per vincere questa forza peso. Essendo questa una posizione di equilibrio instabile, il peso stesso della vettura tenderà a far tornare il punto nelle condizioni iniziali, di ruota diritta. Si genera, quindi un effetto di autoallineamento della ruota che è favorevole durante la marcia rettilinea, perché ogni forza perturbatrice che tende a far deviare la ruota dalla posizione rettilinea deve far alzare la vettura, dando anche alla vettura una “centratura” in marcia, e durante la sterzata a bassa velocità, perché genera un momento autoallineante. Però, implica un aumento di sforzo al volante.
A questo punto, perché la soluzione camber positivo + inclinazione del montante risulta essere penalizzante?
Perché:
- il camber positivo all'anteriore induce sottosterzo
- il camber, comunque, provoca consumo anomalo del pneumatico. se poi è elevato, ancora peggio
- una configurazione del genere, col camber positivo, fa perdere molto feeling di sterzo. lo sterzo risulta molto leggero soprattutto nella zona intorno allo zero volante...ti sembra di galleggiare.
E se invece avessi braccio a terra negativo, cosa succederebbe?
Siccome la ruota NON può staccarsi da terra, sarà la scocca ad abbassarsi.
lo sforzo per ruotare l'auto sarà minore (ma non nullo).
ma avrò una minore centratura dell'auto, perché il peso non mi aiuta più come prima.
questo, naturalmente, tutto in teoria; ammesso che abbia camber positivo etc.
storicamente, il braccio a terra negativo nasce per le trazioni anteriori perché più inclino il king pin più mi avvicino ad avere un BRACCIO AL CENTRO RUOTA nullo (o comunque minore che con braccio a terra positivo) e quindi, minimizzo le reazioni allo sterzo conseguenti alle forze di trazione.
Il camber ha anche un effetto collaterale sul comportamento del veicolo.
Se inclino la ruota, cioè le faccio avere camber, anche l'asse attorno a cui ruota si inclina. una ruota dritta ha l'asse di rotazione parallelo al terreno. una ruota con camber ha asse di rotazione inclinato.
La sua tendenza naturale non è quindi quella di rotolare diritta. siccome è costretta dalle sospensioni ad avere camber, reagirà con delle forze trasversali.
Se immagino che la ruota sia inclinata verso destra, cioè con la parte superiore a destra rispetto alla inferiore e la vedo da dietro che ruota in avanti, la forza trasversale che si genera mi spingerà la ruota verso destra.
Ora, sul dritto, se le ruote dx e sx hanno lo stesso camber, le spinte si elidono e la macchina va dritta. Ma in curva, prevarrà la ruota più carica (quella esterna alla curva) che guiderà l'auto.
Allora avremo:
- con camber negativo: le ruote tirano verso l'interno (della macchina), quindi caricando la ruota esterna (alla curva) avrò la macchina che tirerà verso l'interno (sovrasterzo).
- con camber positivo: le ruote tirano verso l'esterno (della macchina), quindi caricando di più la ruota esterna (alla curva) avrò la macchina che tirerà verso l'esterno (sottosterzo).
Esaurita la vista trasversale, vediamo adesso I parametri che caratterizzano la vista laterale.
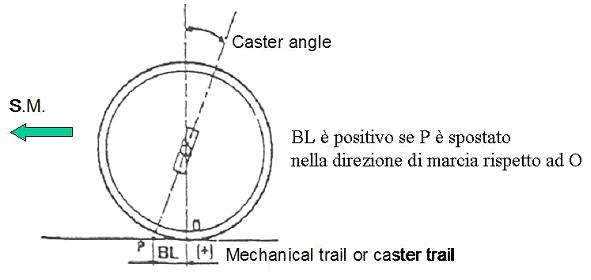
- Incidenza del montante (o chasse, o caster): l’angolo, nella vista laterale appunto, formato dall’asse di sterzo e la verticale della ruota al terreno. Si misura in gradi. E’ positivo se il prolungamento cade davanti alla ruota; negativo, invece, se cade dietro.
Ciò determina il braccio a terra longitudinale, la distanza tra il punto a terra della ruota e l’intersezione dell’asse di sterzo col terreno. è il BL del disegno.
Come influiscono questi parametri sul comportamento del veicolo?
Beh, riguardo all'angolo di caster, detto anche angolo di incidenza longitudinale, (che io chiamerò chasse) è semplice: avete presente i choppers? Bene, i choppers sono moto fatte per andare diritte. e basta.
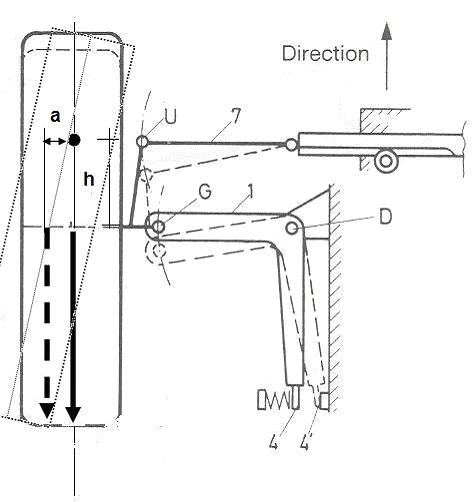
Infatti, la stabilità di una sospensione è direttamente proporzionale al valore (positivo) del braccio a terra longitudinale. Perché?
Guardate l’immagine sottostante, con la sospensione vista dall'alto.
Il pallino indica il punto di intersezione dell'asse di sterzo con il terreno.
La freccia è la forza resistente del pneumatico, come sempre applicata nel punto di contatto della ruota col terreno.
h è la distanza tra il punto di intersezione dell'asse di sterzo e il punto a terra del pneumatico, cioè il braccio a terra longitudinale.
Sul dritto, si ha un momento stabilizzante: la forza sta sulla retta congiungente il punto a terra del pneumatico col punto di intersezione del montante.
Insomma, si crea un MOMENTO STABILIZZANTE M = F a che annulla ogni tentativo di deviazione della ruota (zona tratteggiata).
Il braccio a terra longitudinale DA’ STABILITA’ DIREZIONALE alla vettura (più ancora dei bracci a terra trasversali che abbiamo visto nei giorni scorsi: ecco perché stamattina vi ho detto di lasciare perdere tutte le seghe mentali sul braccio a terra trasversale negativo…)
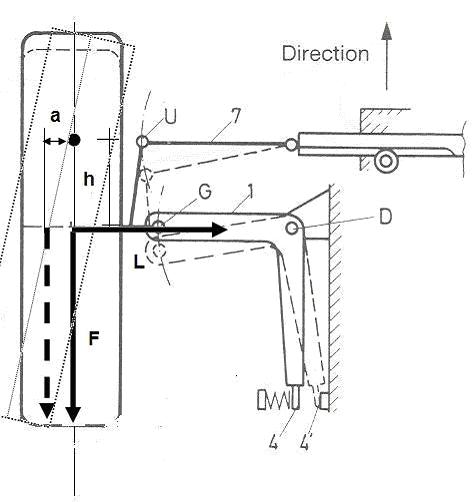
Adesso vediamo cosa succede in curva: la stabilità e il riallineamento automatico della ruota in posizione diritta viene esaltato dalla presenza della forza laterale L. (figura sotto)
Sulla ruota agirà un momento stabilizzante Ms = F a +L h
dove F è la resistenza e L la forza laterale (di aderenza del pneumatico).
Come vedete, la parte di momento raddrizzante (riallineante) dovuta alla forza laterale è NETTAMENTE prevalente e, cosa molto importante, PROPORZIONALE alla forza laterale, cioè alla severità della curva che il guidatore imposta.
Tanto più severa la curva, tanto maggiore il momento autoallineante, tanto più forte la RESISTENZA (l'inerzia) della macchina ad impostare la curva, tanto maggiore lo sforzo del conducente sul volante per farla girare (se non ho servosterzo), tanto maggiore la tendenza della macchina a RIALLINEARSI.
Questo vuol dire che la macchina con angolo di incidenza positivo è in condizioni di STABILITA', è più stabile di una con poco angolo di incidenza, perchè si oppone maggiormente ad ogni tentativo di spostarla da tale condizione.
Abbiamo visto che l'inclinazione trasversale ha un certo effetto stabilizzante.
Adesso, c'è anche l'angolo di incidenza longitudinale: i tecnici (progettisti e collaudatori) hanno dunque un'altra arma per generare lo stesso effetto. possono scegliere l'uno o l'altro per ottenere ciò che vogliono. li possono dosare al meglio.
il momento autoallineante è, come detto, proporzionale alla forza laterale L, che a sua volta è proporzionale al peso agente sulla ruota.
Un altro effetto favorevole alla tenuta di strada e alla stabilità si ha durante le curve: con incidenza positiva, in curva la ruota SI OPPONE al ribaltamento perché la ruota assume sempre più angoli di camber negativi (guardate le Mercedes a ruote completamente sterzate, guardate come si dispone la ruota esterna; e poi, guardate la ruota interna!!). tale effetto è opposto a quello dato dall'inclinazione del montante, per cui la ruota assume angoli di camber sempre più positivi (avevamo parlato della regata, ricordate?): in termine da collaudatori si usa dire che "la macchina prende sotto"...
Considerazioni.
Prima considerazione: tutto quello che abbiamo detto finora si riferisce a sospensioni anteriori. Nulla vieta, tuttavia, di considerarlo valido anche per le sospensioni posteriori. naturalmente, se si tiene conto del fatto che la sospensione posteriore NON sterza (NON è vero, ma per il momento, consideriamolo valido): insomma, se si considera che la sospensione posteriore ha solamente 2 GRADI DI LIBERTA'.
A questo proposito, e per portare un esempio concreto riguardo l'ultimo argomento affrontato in ordine di tempo, vorrei porre alla vostra attenzione il fatto che, se guardate sull'Eper, troverete che i categorici associati alla traversa che regge la sospensione posteriore sono differenti, a seconda che si tratti di traversa per la 147 "normale" e traversa per 147 GTA. Tralasciando il fatto che una è di acciaio e l'altra di alluminio, il motivo della differenza è il seguente: quella della GTA è più inclinata e costringe la sospensione posteriore ad una chasse maggiore. questo perché si è ricercata una maggiore centratura della vettura, stanti le prestazioni maggiori.
Ciò porta alla seconda considerazione: quando diciamo che i bracci a terra hanno certi vantaggi, che il braccio a terra longitudinale (in una sospensione anteriore) è voluto perché offre maggiore centratura, siamo tutti d'accordo e queste considerazioni sono certamente vere. però, ricordatevi che a guidare la macchina è LA SOSPENSIONE POSTERIORE!! la centratura, la prontezza d'inserimento; la tenuta di strada; la maggior parte (se non tutte) delle caratteristiche, delle qualità, dei problemi che affliggono lo sterzo dipendono dalla sospensione posteriore!!! questo deve essere molto chiaro. poi, vedremo il perché.
Non crediate che il comportamento sovrasterzante o sottosterzante di una vettura dipendano dalla maggiore o minore capacità della sospensione anteriore di spingere e assorbire i carichi trasversali...toglietevelo proprio dalla mente! la sospensione anteriore indica la direzione; ma è il posteriore che "esegue" tutto; nessuna (ripeto: nessuna) auto sportiva degna di tale nome (soprattutto se supersportiva) sarà una macchina in cui il posteriore sia "debole"; per cui, NON date retta a TOP GEAR o riviste/trasmissioni simili, spesso di origine inglese, che esaltano le vetture sovrasterzanti e garantiscono valutazioni eccellenti solo se l'auto "va via di culo". Domandatevi perché le F1 e le vetture da gara hanno gomme differenziate, con quelle posteriori più larghe....le F1 sono assi il cui obiettivo è quello di massimizzare la trazione bilanciando il sottosterzo.
Passiamo ora alla vista in pianta.
Convergenza. è l’angolo formato nella vista in pianta, tra l’asse longitudinale del veicolo e l’asse passante per la mezzeria della/e ruota/e
OGNI ruota ha un PROPRIO valore di convergenza. Sommando i singoli valori ho la CONVERGENZA TOTALE.
Quando le ruote convergono nel senso di marcia, si parla di convergenza POSITIVA. Viceversa, di convergenza negativa, o divergenza.
Normalmente, viene fornita la convergenza totale dell’asse in gradi. Più spesso, però, si preferisce darla in millimetri: in pratica, è la differenza tra la distanza tra il cerchio sinistro e quello destro misurata davanti e dietro al mozzo all’altezza del centro ruota.
Due considerazioni:
1- in questo caso, la convergenza in millimetri viene misurata rispetto al CERCHIO DI RIFERIMENTO (che solitamente è il cerchio ruota con cui viene fatto lo sviluppo dell’auto). Tanto per intenderci, sulla GTA il valore di convergenza totale anteriore è -2 mm. (ossia le ruote divergono di 2 mm) misurata sul cerchio di riferimento da 17”: se monto i 18” questo valore di -2 non andrà più bene (sarà maggiore!).
2- in caso di misura di convergenza PARZIALE in millimetri, la differenza del singolo cerchio, destro o sinistro, è riferita all’asse longitudinale del veicolo.
L’impostazione del valore di convergenza dipende da tre fattori:
1- agendo sulla convergenza si agisce direttamente sul comportamento del veicolo in curva: la convergenza è uno dei più importanti fattori/parametri di messa a punto per ottenere il comportamento voluto (sovra o sottosterzatura), che va dosato per raggiungere il COMPROMESSO finale.
2- Impostando il valore di convergenza in condizioni statiche si deve tenere conto del valore che si avrà a vettura in movimento a causa delle forze che agiscono sulla sospensione durante la marcia. Ricordate il discorso dei bracci a terra e delle forze R e di trazione che agiscono durante il moto del veicolo? Ecco, queste forze, meglio: questi momenti, che tendono a far ruotare la ruota vanno tenuti in considerazione nell’impostazione della convergenza!
Es: se ho una TP con l’avantreno con braccio a terra trasversale negativo, devo stare attento a impostare un valore di convergenza positivo, perché poi, col movimento, la convergenza tenderà ad aumentare!! Viceversa, se ho braccio a terra trasversale positivo, la ruota folle tenderà a divergere in movimento per cui per avere convergenza nulla in marcia dovrò dare convergenza positiva. Se le ruote sono motrici, il problema si complica ulteriormente, perché ho anche la forza di trazione (che agisce sulla stessa retta di applicazione della Resistenza, ma il momento si misura rispetto al braccio a terra a centro ruota. Comunque, a livello teorico, il ragionamento è analogo al caso di ruota folle.
3- La convergenza (ma questo lo saprete sicuramente!) incide parecchio sull’usura dei pneumatici. Se guardate la figura qui allegata, vedete che il pneumatico seguirebbe naturalmente la traiettoria tracciata dalla retta passante per il suo centro (e disegnato). Dopo un giro, dovrebbe trovarsi in A; invece, la vettura lo costringe a trovarsi in B. Ad ogni giro, la ruota compie una traslazione (strisciamento) laterale che si traduce in usura del pneumatico. Ecco perché, almeno in teoria (noi infatti siamo i primi a non farlo, perché prediligiamo – o meglio: prediligevamo! - l’handling) occorrerebbe dare valori di convergenza statica tali da avere convergenza zero in marcia.
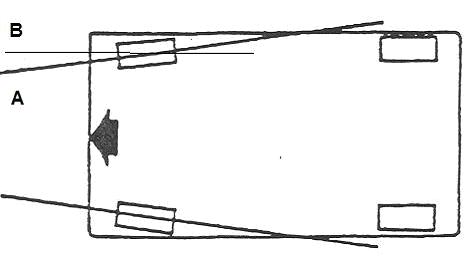
:grazie) Alfistavero.
Per sospensione s'intende quel complesso di elementi che collega la ruota al veicolo, nella maniera più sicura e confortevole per i passeggeri e assicurando alla ruota i gradi di libertà necessari per consentire al veicolo di muoversi.
Cosa sono i gradi di libertà di un corpo e QUANTI sono i g.d.l. di un corpo nello spazio?
I gradi di libertà corpo sono il numero di variabili necessarie per determinare univocamente il suo movimento nello spazio, cioè il numero di coordinate necessario a descrivere il suo moto.
Un corpo nello spazio ha 6 gradi di libertà: 3 traslazioni (secondo gli assi x,y,z) e 3 rotazioni (sempre attorno agli assi x,y,z)
Ogni volta che introduco un grado di vincolo, riduco i gradi di libertà.
Esempio: un corpo su un piano ha 3 g.d.l. Se fisso uno dei punti del corpo, per esempio lo inchiodo, aggiungo 2 gradi di vincolo: può solo ruotare (attorno al punto).
Funzioni svolte dalle sospensioni.
Tenendo conto degli scopi e delle esigenze dell'auto, vediamo di analizzare le funzioni svolte dalle sospensioni.
In primo luogo, poiché la macchina deve potersi muovere e poiché il movimento è assicurato dal rotolamento della ruota, la FUNZIONE PRIMARIA della sospensione è quella di consentire alla ruota di ROTOLARE!!! sarà una banalità, ma questa è la prima cosa: la sospensione deve lasciare alla ruota sicuramente un grado di libertà: la rotazione attorno al proprio asse.
Inoltre, siccome la macchina deve muoversi in ogni direzione, e poiché il cambio di direzione lo si realizza nella maniera più semplice facendo sterzare la ruote (ma non solo), la SECONDA funzione della sospensione è di consentire alla ruota di sterzare!! Cioè, deve lasciare un secondo grado di libertà: la rotazione rispetto ad un asse verticale.
Infine, siccome la macchina si muove sul terreno in ogni direzione, magari in modo confortevole, la TERZA funzione della sospensione è quella di assorbire le asperità della strada, filtrando gli urti e le forze che si generano dal fondo stradale (magari, con qualche elemento che assorbe e dissipa energia; poi vediamo quali...). quindi, deve consentire alla ruota di muoversi in senso verticale, cioè deve lasciare un terzo grado di libertà: il movimento verticale.
Ora, poiché nella macchina le ruote sterzanti sono quelle anteriori, semplificando possiamo dire che la sospensione deve lasciare alla ruota anteriore 3 gradi di libertà; alla ruota posteriore 2 gradi di libertà. in realtà, non è proprio così, se pensate che al posteriore in fase di movimento verticale la ruota è soggetta anche a recuperi di convergenza, quindi a una (seppur minima) sterzatura.
ma per ora, a noi va bene questa schematizzazione di base.
Ora, dal punto di vista FUNZIONALE, quali compiti deve assolvere la sospensione?
La prima è: collegare la ruota alla scocca lasciando i gradi di libertà che servono (alla ruota anteriore e posteriore, cioè 3 e 2).
La seconda: trasformare in energia le asperità incontrate nel movimento sulla strada.
La terza: dissipare, in qualche modo, questa energia.
Per cui, quel complesso di organi (poi vediamo quali) che costituiscono la sospensione può essere formato da elementi diversi come numero, forma disegno etc, e disposti in moltissimi modi. MA DOVRANNO SEMPRE ASSOLVERE AI COMPITI DETTI PRIMA.
Funzionalmente, quindi, gli elementi che costituiscono una sospensione si suddivideranno in:
PORTANTI (che collegano la ruota alla scocca e assicurano i gradi di libertà), per es i bracci oscillanti, i fuselli, gli snodi, tiranti e puntoni
ELASTICI (che collegano elasticamente la ruota, per es. molle, barre di torsione, elementi in gomma come i tamponi)
DISSIPATORI (che dissipano l'energia assorbita dalle asperità, per es. ammortizzatori idraulici.........ma anche le balestre, che sono sia elastiche che dissipatrici.... però, lasciamo perdere. pensate solo agli ammortizzatori.)
Per semplicità, dividiamo le sospensioni in ANTERIORI e POSTERIORI.
Allora, abbiamo visto che ci sono delle funzioni che la sospensione deve svolgere. e il progettista deve, sempre e in ogni caso, progettare delle sospensioni che tengano conto di queste esigenze funzionali (sennò, che cavolo di progettista sarebbe?), e può farlo con grande libertà (almeno teoricamente). Unico vincolo, ripeto ancora perché vi entri in mente, rimane il soddisfacimento delle 3 funzioni principali. però questo non basta, perchè bisogna soddisfarle:
1) nella maniera più affidabile (sennò poi ci troviamo gente che si lamenta ogni volta che salta da un ponte sentendo il gnek gnek del tampone di fine corsa);
2) nella maniera più semplice per la fabbricazione (sennò come farebbe il costruttore a guadagnarci);
3) con il minimo peso (sennò, la gente si lamenta perché la macchina pesa troppo), con il minimo costo (sennò come fanno a darci l'aumento di stipendio?), con il minimo ingombro (sennò facciamo un carro armato, non una macchina);
4) in modo da non penalizzare gli organi a cui ci si attacca (la scocca);
5) offrendo il massimo delle prestazioni tecniche richieste dalla vettura che si sta progettando.
I tipi di sospensione ANTERIORE che si sono salvati a questa serie di VINCOLI (ho fatto apposta ad usare questa parola) importanti e che li soddisfano al meglio, almeno allo stato attuale delle cose, sono 2:
a) sospensione a quadrilatero (e qui ci mettiamo anche il quadrilatero alto della 156/147, perché tecnicamente concettualmente analogo)
b) Mc Pherson
Questo non significa che non possano essere adottati differenti schemi sospensivi per l'avantreno: per esempio, moltissime fuoristrada, di quelle vere hanno un bel ponte rigido, di cui parleremo più avanti- L'Unimog (Mercedes) ha ponti (davanti e dietro) del tipo a U (di cui poi parleremo, dopo il ponte rigido).
Le sospensioni sono suddivise in due grandi classi: a ruote indipendenti e dipendenti.
Le prime sono prive di connessione meccanica tra lato destro e sinistro dell’assale; una forza agente su uno dei lati non ha pertanto effetti sull’altro. Un’altra importante distinzione, all’interno di questa categoria, separa le sospensioni sterzanti da quelle non sterzanti.
Chiaro che il ponte rigido sia una sospensione a ruote dipendenti. le altre che abbiamo descritto, a ruote indipendenti.
Sospensione a quadrilatero

Come si vede la ruota è calettata su un montante (quello che viene descritto con hub) tramite cuscinetti. E qui abbiamo il primo grado di libertà
Il montante, a sua volta, è collegato ai bracci oscillanti (C e D) tramite snodi.
Quindi, il complesso ruota-montante può ruotare attorno ad un asse passante per i due snodi (l'asse di sterzo, tratteggiato e passante per C e D): e qui abbiamo il secondo grado di libertà.
Il complessivo ruota-montante è anche collegato alla scocca tramite attacchi collegati alla scocca stessa (A e B) e quindi può ruotare attorno a quegli attacchi (terzo grado di libertà).
Quelli descritti sono TUTTI organi portanti, mancano gli organi dissipatori e quelli elastici (cioè, rispettivamente, ammortizzatori e molle).
Precisazione: nel disegno del quadrilatero è indicato l'asse di sterzo: vorrei precisare che, affinché sia consentita la sterzata della ruota, i bracci che compongono la sospensione devono convergere (sia quelli superiori, sia quelli inferiori) in un punto; e che la congiungente dei due punti in cui convergono i bracci è appunto l'asse attorno al quale ruota il montante che regge la ruota.
La precisazione potrebbe essere banale, ma non lo è. Infatti, nel caso di sospensione posteriore, i bracci, superiori e inferiori, NON convergono in un punto, ma si dispongono parallelamente (o quasi, poi vedremo come e perché; ma per adesso supponiamo che sia così) gli uni agli altri. in questo caso, NON esiste un asse di sterzo e, infatti, la ruota NON sterza. Oddio, in realtà potrebbe verificarsi il caso che anche al posteriore io possa realizzare una sospensione a quadrilatero utilizzando due TRIANGOLI (uno inferiore e l'altro superiore) che, quindi, realizzano un asse di sterzo. In questo caso, allora, avrò bisogno di un ulteriore braccio che "blocchi" (diciamo così, anche se non è proprio vero; poi anche in questo caso vedremo come si comporta...) la sterzata della ruota posteriore: in questo caso, tale braccio prenderà il nome di "braccio antisterzo" o "finto sterzo".
Sospensione Mc Pherson
Anche qui la ruota è calettata su un montante tramite cuscinetti (primo grado di libertà); Il montante e’ il componente sul quale viene ricavata la sede per alloggiare l’anello esterno del cuscinetto ruota.
Il montante ora è però fissato RIGIDAMENTE all’ammortizzatore.
Alla base del corpo dell’ammortizzatore è saldata una staffa che consente, tramite due bulloni, il collegamento rigido con il montante.
Il complessivo ruota + montante(mozzo) + ammortizzatore può ruotare per l’asse passante per lo snodo sferico (la testina) e per il centro dell’attacco superiore dell’ammortizzatore (secondo g.d.l.): questo è l’asse di sterzo.

Infine, il complessivo di prima può RUOTARE attorno all’attacco sulla scocca (il braccio inferiore è collegato attraverso lo snodo sferico al montante): terzo g.d.l. Quindi, la ruota e’ guidata durante l’escursione verticale dal braccio inferiore (spesso un triangolo, detto triangolo inferiore) che RUOTA (lo ripeto, così si capisce bene) e da un dispositivo a scorrimento lineare di cui e’ parte integrante l’ammortizzatore.
La sospensione Mc Pherson è la più diffusa soprattutto per gli assali anteriori e trova applicazione su (quasi) tutti i veicoli di dimensioni contenute (segmenti A e B). Alcuni costruttori adottano però questa soluzione anche su vetture di segmento superiore, come Porsche, BMW e Jaguar.
Il triangolo inferiore e’ collegato alla scocca o alla traversa di meccanica in due punti, tramite boccole elastiche.
Sul corpo dell’ammortizzatore viene saldato il piattello appoggio molla inferiore. Le spire superiori della molla poggiano su un cuscinetto reggispinta, la cui parte superiore poggia sul tassello duomo. Il tassello e’ il componente di interfaccia dello stelo dell’ammortizzatore e della molla con la scocca. Il collegamento avviene elasticamente al fine di filtrare le vibrazioni.
Differenze tra quadrilatero e Mc Pherson.
Riguardate i 2 disegni, del quadrilatero e del Mc Pherson.
Nel quadrilatero, ogni organo svolge una funzione sola: la molla fa l'elemento elastico; l'ammortizzatore l'elemento dissipatore; i bracci, gli organi portanti e di collegamento.
Però, si può fare in modo che lo stesso organo svolga più funzioni. per esempio, si può sfruttare la grande rigidezza in certe direzioni di una balestra per farle svolgere anche la funzione di organo portante (pensate alla 126)...
sulla strada della semplificazione e della funzione multiruolo dei componenti, si può andare oltre. per esempio, possiamo prendere l'organo dissipatore (cioè l'ammortizzatore) e fargli svolgere funzioni portanti.

Partendo da una sospensione a quadrilatero si arriva alla McPherson semplicemente sostituendo il montante F, il braccio superiore infulcrato in A e l'ammortizzatore che ho disegnato all'interno e indicato con "prima" con un gruppo montante-ammortizzatore che svolge le funzioni di organo portante e dissipatore assieme.
Prima conseguenza: il McPh è funzionalmente più SEMPLICE del quadrilatero. anzi, si può vedere che con il McPh si può giungere a delle semplificazioni estreme semplicemente sostituendo il braccio inferiore con un organo elastico (e quindi portante) come una balestra (come ho già detto prima: vedete la sospensione anteriore della 126).
Si arriva cioè alla semplificazione estrema, dove non ci sono più organi puramente elastici e puramente dissipatori, ma in cui elementi elastici e dissipatori sono ANCHE portanti.
Vediamo di riassumere quali sono i punti a favore e quelli contro tra quadrilatero e McPh.
1) affidabilità: direi McPh, proprio perché ha meno pezzi (Colin Chapman diceva che tutto quello che non c’è non si può rompere. Io condivido in toto)
2) semplicità: sicuramente, è favorito il McPh, che ha meno elementi del quadrilatero (in pratica, una testa a snodo e il braccio oscillante). Meno pezzi = maggiore semplicità. Anche perché il McPh ha meno punti di collegamento alla scocca. E, soprattutto, li ha disposti in punti più lontani fra loro. Questo significa, poi lo vedremo, minori carichi sulla scocca a pari forze generate dal pneumatico (provenienti dal terreno). Quindi, scocca più leggera. Questo è il motivo per cui Porsche l’ha adottata, sia sulla 911 sia sulle altre (Cayman e compagnia bella).
Ora, questo è sicuramente vero almeno finché si considera il quadrilatero classico. Ma dall’introduzione del quadrilatero “alto” (quello della 147 e 156, per intenderci), che sfrutta gli stessi punti di collegamento alla scocca del McPh, i giochi, sotto questo aspetto, sono praticamente alla pari…
3) spazio disponibile per il vano motore: vince il McPh perché ha eliminato l’ingombro del braccio oscillante (del triangolo, se preferite chiamarlo così) superiore. Infatti, questa soluzione è la preferita dalle vetture a trazione anteriore e motore trasversale: il motore trasversale sottrae molto spazio in trasversale, appunto. E se volessimo fare una macchina col quadrilatero, questa finirebbe per diventare larghissima: quindi, bisogna optare per una sospensione che occupi poco spazio in trasversale. Ecco perché gli scontenti del McPh (cioè Alfa e Honda, adesso vediamo perché scontenti) sono andati verso il quadrilatero alto…
4) costo: forse il motivo principale della grande diffusione del McPh. Fare un McPh costa meno in termini di componenti e di scocca (per il motivo visto prima)…
Sembrerebbe prevalere il McPh, dunque. Però, ci sono anche dei punti a favore del quadrilatero.
1) con il quadrilatero, variando opportunamente la lunghezza e l’inclinazione dei bracci si può ottimizzare meglio che con il McPh la variazione degli angoli caratteristici delle ruote con lo scuotimento: si possono controllare meglio le variazioni di questi angoli. Si può controllare meglio la posizione della ruota nel suo movimento. Ora, siccome il controllo degli angoli caratteristici delle ruote è la condizione PRIMARIA per ottenere il comportamento voluto dell’auto (il miglior handling, ma anche il miglior confort, la migliore stabilità, etc).
2) il McPh presenta, inoltre, un’isteresi maggiore del quadrilatero. Se guardate la figura del McPh, vedete che utilizza, per costruzione, il gruppo stelo ed ammortizzare per guidare il cinematismo della sospensione durante gli scuotimenti verticali della ruota. Questa caratteristica costruttiva comporta che i carichi esterni applicati alla ruota determinano, in funzione dell’architettura della sospensione e del posizionamento della molla, una forza laterale ed un momento applicato sullo stelo.
Le reazioni (vincolari) e le rotazioni dovute all’inflessione dello stelo dell’ammortizzatore in corrispondenza delle guide dell’ammortizzatore determinano l’isteresi del componente, dove per isteresi si intende il valore di forza verticale applicata a terra in grado, vincendo gli attriti, di muovere l’ammortizzatore, a partire da una posizione di equilibrio, che è quella statica con la ruota appoggiata a terra (sotto carico statico, appunto)
Tale grandezza, poiché influenza in modo significativo il comportamento del veicolo su fondi stradali con piccoli asperità, rendendo l’auto meno confortevole e “fluida”, deve essere minimizzata in fase di progetto.
Ecco dunque che, con questi aspetti fin qui enunciati ABBIAMO SPARATO IN FRONTE AL MCPHERSON UCCIDENDOLO ALL’ISTANTE!!
Non sarà mica un caso che il quadrilatero trovi applicazione sulle vetture sportive e sulle berline di lusso, in quanto consente una messa a punto dei parametri elastocinematici, in grado di garantire un ottimo compromesso tra prestazioni comfort ed handling.
Nel quadrilatero, l’ammortizzatore non svolge una funzione strutturale (come nel McPh) di sostegno dei carichi statici ma si limita ad avere compiti dissipativi. Sono pertanto ridotti i fenomeni isteretici, penalizzanti il comfort. Oh, questo anche sulle Ferrari, eh!!
L’unica roba che mi dispiace è anche di aver detto, in pratica, che la Porsche utilizza uno schema di sospensioni economico, non “elegante”, non tecnicamente appagante. Mi dispiace proprio, perché per me l’unico difetto che hanno le Porsche è rappresentato da…I PORSCHISTI!!!
Tra l’altro, questo spiega anche il gran lavoro di messa a punto che la Porsche fa: essendo più difficile il controllo degli angoli col McPh, è più difficile riuscire ad ottenere il comportamento che si vuole da una macchina col McPh….
Quindi la messa a punto del McPh (sempre se si vuole fare un bel lavoro e non ci si accontenta) è decisamente più laboriosa e difficile che col quadrilatero….Chiaro che, se ci si accontenta (diciamo che nessuno che acquista una Daewoo Matiz sta lì a farsi problemi se il recupero di camber in sterzata non consente di avere una linearità di sterzatura da primato….).
Sospensione ad assale rigido
Allora, 3 foto: la prima, quella di un assale rigido (quello della Y10) posteriore; la seconda, di un assale che diventa "ponte" perché garantisce anche trazione ed è anteriore perché ha le ruote sterzanti; il terzo, che preferisco, è quello delle Alfa Nord (serie 116 e derivate, cioè Alfetta & Co.): posteriore e "ponte" (tra l'altro, De Dion)
Le tre foto per dirvi che NON è importante la forma dell'asse, ma COME i bracci lavorano e assolvono al compito che gli è assegnato.

La ruota è fissata direttamente al ponte, attraverso un mozzo e cuscinetti ed è libera di rotolare (primo grado di libertà).
il mozzo, a sua volta, è fissato al ponte in modo rigido nel caso di assale posteriore; oppure, attraverso vincoli rigidi (cuscinetti) che consentono alla ruota di ruotare attorno al proprio asse verticale (secondo grado di libertà, nel caso di sospensione anteriore)
infine, il ponte (tutto) può muoversi in senso verticale (in su o in giù, entro certi limiti): terzo grado di libertà.
Secondo me, e non solo secondo me, il ponte rigido è uno dei più bei sistemi di sospensione perché abbina la semplicità alla facilità di costruzione alla possibilità di mantenere corretti gli angoli delle ruote.
Tra i suoi punti forti ci sono, infatti:
1- semplicità di costruzione
2- leggerezza, soprattutto se, nel caso di configurazione "a ponte", cioè asse con trazione, si separa la parte di trasmissione del moto (differenziale, etc) spostandola dalla parte delle masse sospese: tipico il caso del De Dion Alfa....
3- mantenimento degli angoli delle ruote, soprattutto: mantenimento della perfetta perpendicolarità delle ruote rispetto al terreno
4- mantenimento della scocca distante dal terreno quando si affrontano gli ostacoli
Contro:
1- scarsa escursione della sospensione in caso di supermento degli ostacoli, soprattutto quando si ha una configurazione "a ponte" (il differenziale rompe le balle)
2- variazione concorde della campanatura delle 2 ruote (dx e sx) quando una delle due affronta un ostacolo; questo fa nascere, oltretutto, una coppia giroscopica che si ripercuote sullo sterzo (andatevi a vedere la Faq sui problemi in accelerazione della GTA etc: la spiegazione della reazione giroscopica).
Definizione di massa sospesa e non sospesa
Masse sospese: tutto quello che c'è A MONTE della sospensione
Masse NON sospese: tutto quello che c'è A VALLE della sospensione (cioè ruote, freni, ecc)
La sospensione: metà va nelle masse non sospese; metà nelle masse sospese. Cioè, il braccio lo peso e poi metà del peso lo attribuisco alle masse non sospese e l'altra metà a quelle sospese
Angoli ruote
Siccome abbiamo visto che una delle funzioni della sospensione è quella di collegare la ruota alla scocca e di posizionarla non in modo “qualunque”, ma in un ben determinato modo, per ottenere il comportamento che si vuole, la ruota deve avere angoli precisi CHE VANNO RISPETTATI. Ma perché questi angoli vanno rispettati? Cioè, perché sono così importanti?
Perché se la ruota e i componenti della sospensione non sono posizionati correttamente durante il rotolamento si generano forze non volute le cui risultanti compromettono l'efficacia di assolvimento dei 3 compiti fondamentali della sospensione.

Dunque, guardando la macchina, si nota che l’unico suo collegamento con l’esterno sia la zona di contatto tra il pneumatico e la strada. Ho detto zona e non punto: c’è un motivo, che vedremo dopo.
Adesso, però, supponiamo che sia un punto. Punto di contatto col terreno.
Questo vuol dire che TUTTE le reazioni alle forze messe in gioco dalla macchina o dal conducente come il peso, l’accelerazione, la frenata, le variazioni di traiettoria che fanno nascere forze trasversali, trasferimenti di carico etc, e TUTTE le forze che nascono dagli urti contro gli ostacoli mentre la macchina si sta muovendo sono applicate al PUNTO A TERRA della ruota.
Ora, se leghiamo queste forze ai 2 o 3 (nel nostro caso, visto che parliamo di sospensione anteriore, diciamo 3) gradi di libertà della ruota, tiriamo la conclusione che il punto a terra deve essere tale, cioè messo in posizione tale, da ridurre al minimo le perturbazioni (le reazioni) che tali forze possono provocare sul comportamento dell’auto e gli sforzi che il guidatore deve compiere.
Il punto a terra deve avere quindi una posizione ben definita rispetto agli assi di rotazione della ruota (e agli spostamenti) e questo lo si ottiene dando determinati ANGOLI di impostazione sia alle RUOTE, sia ai suoi ASSI DI ROTAZIONE.
Guardiamo prima i parametri caratteristici che si vedono nella VISTA FRONTALE (e che sono STRETTAMENTE collegati tra loro):
- Camber (o Campanatura): è l’angolo tra la verticale e l’asse passante per la mezzeria della ruota. Positivo quando, come nella figura, la ruota diverge in alto. Negativo, al contrario. Chiaro che si misura in gradi!!!!!
- Inclinazione TRASVERSALE del montante (o King Pin): è l’angolo formato tra la verticale e l’asse di sterzo (cioè la congiungente i due snodi -superiore e inferiore- della sospensione). Anche questo si misura in gradi!!!
Ecco perché, prima, ho scritto PUNTO di contatto a terra tra pneumatico e strada: vedete che prendo sempre la MEZZERIA della ruota? E se suppongo la ruota rotonda (meglio: circolare) e perfettamente rigida, la circonferenza (cioè la mezzeria della ruota) non tocca forse la strada in un punto? In realtà, il contatto tra strada e ruota è una superficie, non un punto (poi lo vedremo). E la ruota NON è indeformabile (anche questo lo vedremo poi).
Guardate questo secondo disegno:

- Braccio a terra trasversale: è la distanza tra il punto a terra della ruota (O in figura) e l’intersezione tra il piano stradale e l’asse di sterzo (il punto P)
Guardateveli bene, questi parametri; perché sono collegati tra loro e, agendo su di essi, si cerca di ottenere sempre il medesimo scopo: RIDURRE l’influenza delle forze verticali (peso, soprattutto; ma anche trasferimenti di carico, deportanza aerodinamica etc) e delle forze longitudinali (frenata e, se stiamo parlando di vetture a trazione anteriore, accelerazione, perché stiamo considerando ruote anteriori; ma le stesse considerazioni valgono se consideriamo ruote posteriori, ovviamente NON sterzanti ma per le quali valgono le stesse, identiche, medesime regole, compreso l’asse di sterzo!!! Ma pure forze perturbatrici conseguenti agli urti contro gli ostacoli) sul comportamento del veicolo.
Il braccio a terra trasversale è BT cioè il segmento O-P
Vediamo allora quali effetti hanno queste grandezze sulle forze che agiscono in marcia (e poi, anche da fermo).
In marcia, dunque, si possono avere forze longitudinali dovute a frenatura e effetti perturbanti dovuti a urti della ruota contro il terreno, forze di resistenza al rotolamento generate dai pneumatici stessi, ect. HO VOLUTAMENTE TRALASCIATO LE FORZE DOVUTE ALLA TRAZIONE! Perché, semplice: lo vedrete tra poco.
Comunque, TUTTE queste forze vengono applicate al punto di contatto tra ruota e terreno. Sono forze che tendono a far oscillare la ruota attorno al suo asse di rotazione.
Osservate la figura:

E’ la sospensione anteriore della 147, vista dall’alto. Il pallino bianco è l’impronta del punto di contatto (a terra) dell’asse di sterzo col terreno. F è la forza longitudinale che, come detto, è applicata al punto di contatto tra ruota e terreno (lungo l’asse della ruota).
Quello indicato con a è il braccio della forza rispetto al punto a terra (è il braccio a terra trasversale, quello che nel disegno della settimana scorsa come BT. Allora, alla ruota viene applicato un momento M= F a.
Ora, se le forze applicate sulla ruota destra e sulla sinistra agissero contemporaneamente (e fossero uguali), il conducente non avvertirebbe nessuno sforzo al volante. In realtà, generalmente, avviene che le forze sono diverse: sia perché, magari, la forza F compare solo su una delle due ruote (per esempio, quando affronto un ostacolo); sia perché la forza F dipende da un sacco di fattori, come il peso, l’aderenza locale, l’equilibrio dei freni, etc..
Quindi, quasi sempre, la realtà ci dice che sulla ruota destra e su quella sinistra agiscono forze di intensità differente. In questo caso, quello reale, avviene che il momento M si ripercuote sulla tiranteria dello sterzo, distante b dal centro di rotazione (che è il nostro punto di contatto col terreno che determina il braccio a terra) della ruota, generando una forza S = M / b cioè F a/b.
Questa forza S tenderà a far ruotare il volante in una determinata direzione. Nel nostro caso, verso sinistra; se invece il braccio a terra fosse negativo, cioè il punto cadesse all’esterno dell’asse ruota, la forza S avrebbe segno contrario e il volante tenderebbe a ruotare a destra. Insomma, col braccio a terra positivo la ruota tende ad aprire in frenata; col braccio a terra negativo la ruota tende a chiudere in frenata e quindi si tende a mantenere la traiettoria, diciamo così…questo è uno dei motivi, per esempio, per cui le macchine dotate di ABS hanno generalmente braccia a terra negativi….
Torniamo alla forza S. Il conducente sarà allora costretto a controbilanciare questa sterzata (che, ricordiamolo, è IMPROVVISA!) con un momento applicato al volante e, nel caso di forze dovute al contatto con ostacoli improvvisi o grandi valori di braccio a terra è estremamente difficile da controllare, perché appunto improvvisa ed elevata.
Un modo per ovviare a tale inconveniente è quello di ridurre la forza S: quindi, si può agire aumentando b (difficile da fare perché ciò significa agire sul cinematismo dello sterzo e questo comporta tutta una serie di altre conseguenze pesanti); oppure, visto che non si può ridurre F, allora si riduce il braccio a terra (a). Ma col McPh è difficile, perché per motivi di spazio (dove metto la molla che è grossa?) il McPh ha sempre una certa inclinazione del montante (king pin). Per ridurlo davvero, devo cambiare sospensione: passo allora al quadrilatero alto: in pratica, sposto il braccio superiore, come ho già detto la settimana scorsa, da dentro la ruota a SOPRA la ruota e sfrutto gli stessi attacchi alla scocca del McPh….
Prima, ho detto: consideriamo solo le forze resistenti, dovute a frenatura, etc.
Bene, tenete ben presente questo: LE FORZE FRENANTI (frenatura, resistenza per attrito, perturbanti, etc) VENGONO APPLICATE NEL PUNTO A TERRA (punto di contatto tra ruota e terreno). INVECE, LE FORZE MOTRICI VENGONO APPLICATE AL CENTRO DELLA RUOTA. Allora, se vogliamo applicare la stessa teoria in caso di forze di trazione, dovremo applicare la nostra forza F al centro della ruota (e nel disegno della sospensione vista dall’alto non cambia nulla a livello di F) e usare, anziché il braccio a terra (la distanza a del disegno qui sopra), il BRACCIO A CENTRO RUOTA
Guardate la foto di settimana scorsa (pagina 8), quando abbiamo discusso sul significato del punto indicato come BTcr… Bene, ADESSO VE LO POSSO SVELARE: è il BRACCIO A CENTRO RUOTA. Anche il braccio a centro ruota deve essere ridotto; SOPRATTUTTO il braccio a centro ruota deve essere minimizzato, perché le coppie (le forze) motrici sono elevate e quindi è più evidente il problema. Bene : questo è il torque steer, (di cui abbiamo parlato nella Faq della 147 GTA).
Dicevamo che ci sono dei modi per ridurre questo braccio a terra. Abbiamo visto, per esempio, che possiamo cambiare sospensione (quadrilatero alto invece di McPh); ma si può anche AUMENTARE IL KING PIN (cioè inclinare di più il montante), oppure inclinare di più la ruota dando campanatura (camber) positiva.
Vediamo. Partiamo da quest’ultima proposta: vi ricordate la Fiat Regata, o la Ritmo? Non avevano forse le ruote davanti con camber positivo? Yes, lo avevano fatto per questo motivo. Peccato però che per ovviare ad un problema se ne era generato un altro: l’usura dei pneumatici, che si consumavano tanto nel bordo che era in contatto col terreno. Chi aha avuto la Regata, mi sa dire quanti treni di gomme anteriori ha cambiato?
In realtà la regata aveva anche il king pin elevato….sennò avrebbe consumato le ruote ancora di più.
Vediamo allora cosa significa aumentare il kingpin.
L’inclinazione del montante genera quel problema di cui si parlava nel 3d della 147 GTA: se ho un kingpin elevato, ho pure in questo caso del torque steer.

L’asse di sterzo tende ad autosterzare se forma un angolo α diverso da 0 con il semialbero (il semiasse) che porta il moto.
Il momento di sterzatura vale Ms = M (BTcr/R + sinφ) dove BTcr è il braccio a centro ruota (dovreste saperlo benissimo, adesso) e R è il raggio di rotolamento della ruota.
Ora, tralasciando il termine BTcr/R, si può scrivere che Ms = M sinφ.
Tanto più è inclinato il montante, tanto maggiore sarà il momento autosterzante (vedi 164 3.0)…Quindi, bisogna raddrizzare ‘sto montante. Ma col McPh è impossibile averlo perfettamente dritto (come con il quadrilatero)….
In realtà, c’è un ulteriore modo di ridurre i bracci a terra (e a centro ruota) col McPh: fare in modo che l’asse di sterzo stia il più vicino possibile all’asse di mezzeria della ruota facendo in modo che il vertice che collega i due bracci che compongono il triangolo inferiore, per esempio, cada “al di là” della ruota. Per fare ciò, bisogna che il triangolo della sospensione NON sia un triangolo fisico, cioè non sia un pezzo unico reale; ma sia composto da due bracci che, opportunamente inclinati, vadano ad incontrarsi in un punto ben determinato che NON è fisico ma VIRTUALE (cioè, lo determini sul foglio da disegno, ma non nella realtà). Un classico esempio è la sospensione ad asse di sterzo semivirtuale (semi perchè il punto sul duomo è reale che più reale non si può) della BMW (es serie 5): beccatevi ‘sta sospensione, curatissima…

Finora abbiamo visto cosa succede se la macchina si sta muovendo.
Vediamo ora che influenza hanno i parametri che abbiamo visti (kingpin, camber e bracci a terra vari) a vettura ferma.
A vettura ferma prevalgono le forze dovute alla resistenza offerta dal pneumatico alla rotazione intorno al suo asse.
Rammento che l’asse di sterzo non è altro che l’asse attorno cui ruota la ruota (scusate il gioco di parole)….
Se ho braccio a terra, tutto il momento M = F a di prima me lo ritrovo nello sforzo che devo applicare al volante.
Se la sospensione non avesse braccio a terra (se cioè fosse nullo il valore del braccio a terra) il punto di intersezione dell’asse di sterzo della sospensione coinciderebbe con il punto a terra di contatto della ruota. Quindi, per sterzare da fermo (o a bassa velocità) la ruota dovrebbe strisciare sul terreno, richiedendo una certa fatica fisica (anche se comunque minore rispetto a prima)
Insomma, comunque la giro, sono fregato!!
Però, il kingpin e la campanatura possono essermi un po’ d’aiuto.
Guardate questa figura: ho prolungato l’asse del camber e quello di sterzo che, in questo caso, si incontrano al di sotto del terreno.

La ruota, tanto per essere chiari, durante la sterzata descrive un cono avente per asse l’asse di rotazione. Esaminando il punto di contatto col terreno, si vede che, a partire dalla posizione di marcia rettilinea dove il contatto avviene sulla superficie stradale, durante la sterzata questo tenderebbe a seguire l’ellisse che ho disegnato: in pratica, il punto di contatto a terra della ruota tenderebbe ad andare SOTTO la linea di terra. Ora, questo NON è chiaramente possibile. Il punto costringe allora la scocca ad ALZARSI vincendone il peso. Parte dell’energia spesa dal conducente per sterzare va appunto per vincere questa forza peso. Essendo questa una posizione di equilibrio instabile, il peso stesso della vettura tenderà a far tornare il punto nelle condizioni iniziali, di ruota diritta. Si genera, quindi un effetto di autoallineamento della ruota che è favorevole durante la marcia rettilinea, perché ogni forza perturbatrice che tende a far deviare la ruota dalla posizione rettilinea deve far alzare la vettura, dando anche alla vettura una “centratura” in marcia, e durante la sterzata a bassa velocità, perché genera un momento autoallineante. Però, implica un aumento di sforzo al volante.
A questo punto, perché la soluzione camber positivo + inclinazione del montante risulta essere penalizzante?
Perché:
- il camber positivo all'anteriore induce sottosterzo
- il camber, comunque, provoca consumo anomalo del pneumatico. se poi è elevato, ancora peggio
- una configurazione del genere, col camber positivo, fa perdere molto feeling di sterzo. lo sterzo risulta molto leggero soprattutto nella zona intorno allo zero volante...ti sembra di galleggiare.
E se invece avessi braccio a terra negativo, cosa succederebbe?

Siccome la ruota NON può staccarsi da terra, sarà la scocca ad abbassarsi.
lo sforzo per ruotare l'auto sarà minore (ma non nullo).
ma avrò una minore centratura dell'auto, perché il peso non mi aiuta più come prima.
questo, naturalmente, tutto in teoria; ammesso che abbia camber positivo etc.
storicamente, il braccio a terra negativo nasce per le trazioni anteriori perché più inclino il king pin più mi avvicino ad avere un BRACCIO AL CENTRO RUOTA nullo (o comunque minore che con braccio a terra positivo) e quindi, minimizzo le reazioni allo sterzo conseguenti alle forze di trazione.
Il camber ha anche un effetto collaterale sul comportamento del veicolo.
Se inclino la ruota, cioè le faccio avere camber, anche l'asse attorno a cui ruota si inclina. una ruota dritta ha l'asse di rotazione parallelo al terreno. una ruota con camber ha asse di rotazione inclinato.
La sua tendenza naturale non è quindi quella di rotolare diritta. siccome è costretta dalle sospensioni ad avere camber, reagirà con delle forze trasversali.
Se immagino che la ruota sia inclinata verso destra, cioè con la parte superiore a destra rispetto alla inferiore e la vedo da dietro che ruota in avanti, la forza trasversale che si genera mi spingerà la ruota verso destra.
Ora, sul dritto, se le ruote dx e sx hanno lo stesso camber, le spinte si elidono e la macchina va dritta. Ma in curva, prevarrà la ruota più carica (quella esterna alla curva) che guiderà l'auto.
Allora avremo:
- con camber negativo: le ruote tirano verso l'interno (della macchina), quindi caricando la ruota esterna (alla curva) avrò la macchina che tirerà verso l'interno (sovrasterzo).
- con camber positivo: le ruote tirano verso l'esterno (della macchina), quindi caricando di più la ruota esterna (alla curva) avrò la macchina che tirerà verso l'esterno (sottosterzo).
Esaurita la vista trasversale, vediamo adesso I parametri che caratterizzano la vista laterale.

- Incidenza del montante (o chasse, o caster): l’angolo, nella vista laterale appunto, formato dall’asse di sterzo e la verticale della ruota al terreno. Si misura in gradi. E’ positivo se il prolungamento cade davanti alla ruota; negativo, invece, se cade dietro.
Ciò determina il braccio a terra longitudinale, la distanza tra il punto a terra della ruota e l’intersezione dell’asse di sterzo col terreno. è il BL del disegno.
Come influiscono questi parametri sul comportamento del veicolo?
Beh, riguardo all'angolo di caster, detto anche angolo di incidenza longitudinale, (che io chiamerò chasse) è semplice: avete presente i choppers? Bene, i choppers sono moto fatte per andare diritte. e basta.
Infatti, la stabilità di una sospensione è direttamente proporzionale al valore (positivo) del braccio a terra longitudinale. Perché?
Guardate l’immagine sottostante, con la sospensione vista dall'alto.
Il pallino indica il punto di intersezione dell'asse di sterzo con il terreno.
La freccia è la forza resistente del pneumatico, come sempre applicata nel punto di contatto della ruota col terreno.
h è la distanza tra il punto di intersezione dell'asse di sterzo e il punto a terra del pneumatico, cioè il braccio a terra longitudinale.
Sul dritto, si ha un momento stabilizzante: la forza sta sulla retta congiungente il punto a terra del pneumatico col punto di intersezione del montante.
Insomma, si crea un MOMENTO STABILIZZANTE M = F a che annulla ogni tentativo di deviazione della ruota (zona tratteggiata).
Il braccio a terra longitudinale DA’ STABILITA’ DIREZIONALE alla vettura (più ancora dei bracci a terra trasversali che abbiamo visto nei giorni scorsi: ecco perché stamattina vi ho detto di lasciare perdere tutte le seghe mentali sul braccio a terra trasversale negativo…)

Adesso vediamo cosa succede in curva: la stabilità e il riallineamento automatico della ruota in posizione diritta viene esaltato dalla presenza della forza laterale L. (figura sotto)
Sulla ruota agirà un momento stabilizzante Ms = F a +L h
dove F è la resistenza e L la forza laterale (di aderenza del pneumatico).
Come vedete, la parte di momento raddrizzante (riallineante) dovuta alla forza laterale è NETTAMENTE prevalente e, cosa molto importante, PROPORZIONALE alla forza laterale, cioè alla severità della curva che il guidatore imposta.
Tanto più severa la curva, tanto maggiore il momento autoallineante, tanto più forte la RESISTENZA (l'inerzia) della macchina ad impostare la curva, tanto maggiore lo sforzo del conducente sul volante per farla girare (se non ho servosterzo), tanto maggiore la tendenza della macchina a RIALLINEARSI.
Questo vuol dire che la macchina con angolo di incidenza positivo è in condizioni di STABILITA', è più stabile di una con poco angolo di incidenza, perchè si oppone maggiormente ad ogni tentativo di spostarla da tale condizione.

Abbiamo visto che l'inclinazione trasversale ha un certo effetto stabilizzante.
Adesso, c'è anche l'angolo di incidenza longitudinale: i tecnici (progettisti e collaudatori) hanno dunque un'altra arma per generare lo stesso effetto. possono scegliere l'uno o l'altro per ottenere ciò che vogliono. li possono dosare al meglio.
il momento autoallineante è, come detto, proporzionale alla forza laterale L, che a sua volta è proporzionale al peso agente sulla ruota.
Un altro effetto favorevole alla tenuta di strada e alla stabilità si ha durante le curve: con incidenza positiva, in curva la ruota SI OPPONE al ribaltamento perché la ruota assume sempre più angoli di camber negativi (guardate le Mercedes a ruote completamente sterzate, guardate come si dispone la ruota esterna; e poi, guardate la ruota interna!!). tale effetto è opposto a quello dato dall'inclinazione del montante, per cui la ruota assume angoli di camber sempre più positivi (avevamo parlato della regata, ricordate?): in termine da collaudatori si usa dire che "la macchina prende sotto"...
Considerazioni.
Prima considerazione: tutto quello che abbiamo detto finora si riferisce a sospensioni anteriori. Nulla vieta, tuttavia, di considerarlo valido anche per le sospensioni posteriori. naturalmente, se si tiene conto del fatto che la sospensione posteriore NON sterza (NON è vero, ma per il momento, consideriamolo valido): insomma, se si considera che la sospensione posteriore ha solamente 2 GRADI DI LIBERTA'.
A questo proposito, e per portare un esempio concreto riguardo l'ultimo argomento affrontato in ordine di tempo, vorrei porre alla vostra attenzione il fatto che, se guardate sull'Eper, troverete che i categorici associati alla traversa che regge la sospensione posteriore sono differenti, a seconda che si tratti di traversa per la 147 "normale" e traversa per 147 GTA. Tralasciando il fatto che una è di acciaio e l'altra di alluminio, il motivo della differenza è il seguente: quella della GTA è più inclinata e costringe la sospensione posteriore ad una chasse maggiore. questo perché si è ricercata una maggiore centratura della vettura, stanti le prestazioni maggiori.
Ciò porta alla seconda considerazione: quando diciamo che i bracci a terra hanno certi vantaggi, che il braccio a terra longitudinale (in una sospensione anteriore) è voluto perché offre maggiore centratura, siamo tutti d'accordo e queste considerazioni sono certamente vere. però, ricordatevi che a guidare la macchina è LA SOSPENSIONE POSTERIORE!! la centratura, la prontezza d'inserimento; la tenuta di strada; la maggior parte (se non tutte) delle caratteristiche, delle qualità, dei problemi che affliggono lo sterzo dipendono dalla sospensione posteriore!!! questo deve essere molto chiaro. poi, vedremo il perché.
Non crediate che il comportamento sovrasterzante o sottosterzante di una vettura dipendano dalla maggiore o minore capacità della sospensione anteriore di spingere e assorbire i carichi trasversali...toglietevelo proprio dalla mente! la sospensione anteriore indica la direzione; ma è il posteriore che "esegue" tutto; nessuna (ripeto: nessuna) auto sportiva degna di tale nome (soprattutto se supersportiva) sarà una macchina in cui il posteriore sia "debole"; per cui, NON date retta a TOP GEAR o riviste/trasmissioni simili, spesso di origine inglese, che esaltano le vetture sovrasterzanti e garantiscono valutazioni eccellenti solo se l'auto "va via di culo". Domandatevi perché le F1 e le vetture da gara hanno gomme differenziate, con quelle posteriori più larghe....le F1 sono assi il cui obiettivo è quello di massimizzare la trazione bilanciando il sottosterzo.
Passiamo ora alla vista in pianta.
Convergenza. è l’angolo formato nella vista in pianta, tra l’asse longitudinale del veicolo e l’asse passante per la mezzeria della/e ruota/e
OGNI ruota ha un PROPRIO valore di convergenza. Sommando i singoli valori ho la CONVERGENZA TOTALE.
Quando le ruote convergono nel senso di marcia, si parla di convergenza POSITIVA. Viceversa, di convergenza negativa, o divergenza.
Normalmente, viene fornita la convergenza totale dell’asse in gradi. Più spesso, però, si preferisce darla in millimetri: in pratica, è la differenza tra la distanza tra il cerchio sinistro e quello destro misurata davanti e dietro al mozzo all’altezza del centro ruota.
Due considerazioni:
1- in questo caso, la convergenza in millimetri viene misurata rispetto al CERCHIO DI RIFERIMENTO (che solitamente è il cerchio ruota con cui viene fatto lo sviluppo dell’auto). Tanto per intenderci, sulla GTA il valore di convergenza totale anteriore è -2 mm. (ossia le ruote divergono di 2 mm) misurata sul cerchio di riferimento da 17”: se monto i 18” questo valore di -2 non andrà più bene (sarà maggiore!).
2- in caso di misura di convergenza PARZIALE in millimetri, la differenza del singolo cerchio, destro o sinistro, è riferita all’asse longitudinale del veicolo.
L’impostazione del valore di convergenza dipende da tre fattori:
1- agendo sulla convergenza si agisce direttamente sul comportamento del veicolo in curva: la convergenza è uno dei più importanti fattori/parametri di messa a punto per ottenere il comportamento voluto (sovra o sottosterzatura), che va dosato per raggiungere il COMPROMESSO finale.
2- Impostando il valore di convergenza in condizioni statiche si deve tenere conto del valore che si avrà a vettura in movimento a causa delle forze che agiscono sulla sospensione durante la marcia. Ricordate il discorso dei bracci a terra e delle forze R e di trazione che agiscono durante il moto del veicolo? Ecco, queste forze, meglio: questi momenti, che tendono a far ruotare la ruota vanno tenuti in considerazione nell’impostazione della convergenza!
Es: se ho una TP con l’avantreno con braccio a terra trasversale negativo, devo stare attento a impostare un valore di convergenza positivo, perché poi, col movimento, la convergenza tenderà ad aumentare!! Viceversa, se ho braccio a terra trasversale positivo, la ruota folle tenderà a divergere in movimento per cui per avere convergenza nulla in marcia dovrò dare convergenza positiva. Se le ruote sono motrici, il problema si complica ulteriormente, perché ho anche la forza di trazione (che agisce sulla stessa retta di applicazione della Resistenza, ma il momento si misura rispetto al braccio a terra a centro ruota. Comunque, a livello teorico, il ragionamento è analogo al caso di ruota folle.
3- La convergenza (ma questo lo saprete sicuramente!) incide parecchio sull’usura dei pneumatici. Se guardate la figura qui allegata, vedete che il pneumatico seguirebbe naturalmente la traiettoria tracciata dalla retta passante per il suo centro (e disegnato). Dopo un giro, dovrebbe trovarsi in A; invece, la vettura lo costringe a trovarsi in B. Ad ogni giro, la ruota compie una traslazione (strisciamento) laterale che si traduce in usura del pneumatico. Ecco perché, almeno in teoria (noi infatti siamo i primi a non farlo, perché prediligiamo – o meglio: prediligevamo! - l’handling) occorrerebbe dare valori di convergenza statica tali da avere convergenza zero in marcia.

:grazie) Alfistavero.

