Ammortizzatori.
Per parlare degli ammortizzatori, occorre conoscere un pochino le derivate di secondo ordine. Chi le conosce, va tranquillo; chi non le conosce, avrà qualche difficoltà in più. Comunque, vedremo di fare le cose semplici semplici, tirandole in ballo solo per il tempo necessario e non oltre.
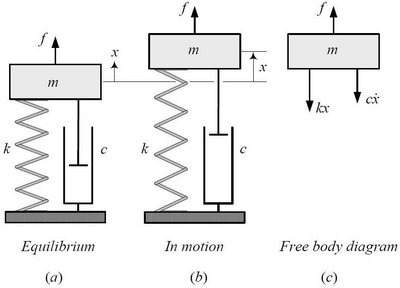
Finora abbiamo visto la nostra macchina appoggiata sulle sospensioni dotate di molle. Diciamo che, se conosciamo (e possiamo conoscerla) la massa che grava sulla singola sospensione, possiamo schematizzare il tutto come nel disegno qui sotto:
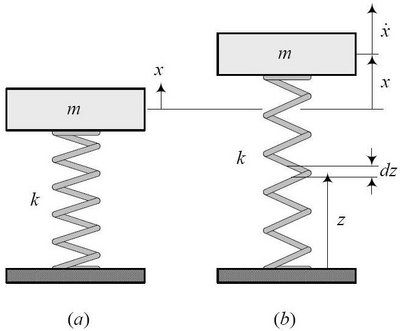
m è la massa sospesa su ciascuna singola sospensione.
Poi c'è la molla, di costante elastica K.
Chiaramente, questo è uno schema semplicissimo, perché ho trascurato tante altre "variabili": per esempio, ho tralasciato il pneumatico, che si comporta anch'esso come una molla (e come un ammortizzatore).
Ad ogni modo, questo è lo schema che descrive, abbastanza bene, il lavoro della mia sospensione (dal punto di vista energetico).
Se la strada mi fa comprimere o estendere la molla, la mia molla si comprime o si estende: quindi, si genera una forza.
Come potete anche vedere, questo è un sistema con 1 grado di libertà (andate a ri-vedervi il discorso delle coordinate libere, dei gradi di libertà e dei gradi di vincolo fatto nella prima Faq sulle sospensioni): la coordinata libera è la mia X: la massa può muoversi solo in verticale.
Quindi, X è lo spostamento. Quello che nel disegno è indicato con X col puntino sopra è la derivata di X rispetto al tempo (dX/dt), cioè la velocità con cui si muove la mia massa all'istante in cui la osservo.
Se guardo la massa a destra, nel disegno sopra, vedo che questa è spostata di una certa quantità (x) rispetto alla posizione indeformata. Questo significa che la mia massa m si sta muovendo rispetto alla posizione di equilibrio (per esempio, perché ho preso una buca, o una sconnessione della strada). Quindi, significa anche che la mia molla, che in condizioni di equilibrio era compressa di una certa quantità per generare una forza che sostenesse il peso della massa m, sta generando una forza F proporzionale alla sua elongazione x. Cioè, F = k x.
Se applico la legge di Newton che recita F = m a (per essere precisi, va però detto che NON ha scritto la sua famosa legge nella forma F = m a , bensì nella forma F = dQ/dt, ossia derivata della quantità di moto rispetto al tempo. Ora, siccome la quantità di moto Q vale Q = m v, la formula di Newton diventa F = m (dv/dt) + v (dm/dt). Noi supponiamo, con buona approssimazione, che la massa m non cambi, per cui il mio termine dm/dt è uguale a 0. Quindi, rimane solo che F = m (dv/dt) cioè F = m a) avrò:
F = k x (anzi a –k x perché la forza elastica si oppone al moto della massa m)
mentre m a diventa m (dv/dt) = m (d2x/dt2) = m x” (con x” ho indicato la derivata seconda dello spostamento).
Quindi:
m x” – k x = 0
cioè x” – (k/m) x = 0
Ora, se pongo ω2 = k/m
riscrivo il tutto come x” - ω2 x = 0
Questa è la legge di moto che descrive, appunto, il movimento della mia massa m sostenuta dalla molla. Ma questa è anche un’equazione differenziale (a coeff. costanti) del secondo ordine.
L’integrale (cioè la soluzione) di questa equazione è:
x(t) = A cos (ωt + φ)
che è l’equazione di un moto armonico.
A e φ sono due coefficienti che dipendono dalle condizioni iniziali del sistema (es. da quando comincio a misurare, etc).
Quello che importa, invece, è il valore ω, che prende il nome di frequenza propria del sistema
e vale, appunto, ω = sqrt (k/m) (ossia radice quadrata di k/m).
Guardiamo l’equazione di moto del sistema molla-massa:
x(t) = A cos (ωt + φ)
Tralasciamo i valori A e φ per il momento.
Concentriamoci sulla frequenza propria, cioè su ω.
Questa vale, come detto SQR(k/m), ossia radice quadrata di k/m, dove:
k è la costante elastica della molla;
m è la massa (della mia porzione di macchina);
ω è dunque la frequenza propria del sistema e si misura in Hertz (Hz).
Chiaro, a questo punto, che io possa determinare anche il periodo di oscillazione, ossia il tempo che intercorre tra due istanti uguali della mia oscillazione. Il periodo è T = 2 / ω
ossia T = 2 * (PIgreco) / SQR(k/m)
Cosa significa tutto ciò?
Che la mia macchina, schematizzata come una massa m su molla k, se sottoposta ad un’azione perturbatrice (irregolarità del terreno), incomincerà ad oscillare. Oscillerà con una certa frequenza, che dipende dalla massa della macchina e dalla rigidezza della molla.
L’accelerazione che subirà la mia massa, cioè la mia scocca (o la parte di scocca di massa m con cui ho schematizzato la macchina) dipenderà dalla frequenza dell’eccitazione dovuta alla strada. Ossia, se la mia strada ha una certa ondulazione e io la percorro avanti e indietro a velocità crescenti, la mia scocca (la massa m) comincerà ad oscillare sempre più. Data la strada e la sua ondulazione, posso modificare la frequenza con cui “eccito” la scocca semplicemente percorrendo la strada a velocità differenti. Provate a pensarci. Supponiamo che cominci a bassissima velocità. La mia scocca inizia ad oscillare piano. Poi aumento un po’ la velocità e la scocca oscilla sempre un po’ di più. La mia scocca sarà sottoposta ad accelerazioni sempre maggiori perché la mia eccitante (la strada ondulata) “eccita”, appunto, sempre più la scocca.
Ad un certo punto, arriverò a percorrere la strada ondulata ad una velocità tale che la frequenza delle mie oscillazioni eccitanti coincidono con la frequenza propria della mia macchina ω = SQR(k/m). In questo caso, l’accelerazione della scocca (cioè della mia massa m) diventerà elevatissima: questo significa che la strada, percorsa a quella determinata velocità, ha eccitato la frequenza propria della mia macchina. Cioè l’eccitante (la strada) ha frequenza pari alla frequenza propria del mio sistema (sistema molla-massa).
Chiaramente, se a quella velocità avessi una macchina diversa (cioè con m diversa) o mettessi una molla diversa (ossia con un diverso k), la mia frequenza propria sarebbe differente (maggiore o minore di prima) e quindi manderei “in risonanza” la macchina ad una velocità differente (maggiore o minore) su quella determinata strada. Precisamente, se aumento la rigidezza k della molla, la mia frequenza aumenterà (k è al numeratore); se aumento m, la mia frequenza diminuirà (m è al denominatore). Se diminuisco l’una o l’altra, succederà il contrario. se modifico l’una E l’altra, dipende dall’entità delle due modifiche.
Questo è quello che succede se viaggio con una macchina dotata solamente di molle (senza ammortizzatori). In pratica, la mia scocca continuerà ad oscillare e, facilmente, mi troverò in condizioni di “risonanza”. E guardate che è abbastanza facile trovarsi in quelle condizioni, perché la frequenza propria della cassa, della scocca, è piuttosto bassa, nell’ordine dell’1,5 Hz. Avete capito bene: 1,5 Hz (la ruota – cerchio + pneumatico - ha invece una frequenza propria di un ordine di grandezza maggiore, quindi siamo nell'ordine dei 15 Hz).
Se proprio vogliamo esagerare e comprendere tutti i tipi di scocca, diciamo che la frequenza propria di una scocca varia tra 1 e 2 Hz (proprio a voler stare larghi). Le frequenza maggiori sono proprie delle vetture con scocca più rigida.
E se mi trovo in condizioni di risonanza, significa che “spicco il volo” con la scocca. Ossia, la mia scocca (e tutto quello che c’è dentro) subirà delle accelerazioni molto elevate.
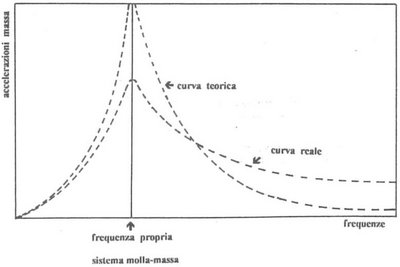
Per farvi capire meglio il problema, allego il grafico seguente.
Sull’asse delle ascisse c’è la frequenza delle mie forze perturbatrici (eccitanti). Affinché comprendiate meglio, fate finta che su quell’asse ci sia la velocità con cui percorrete la strada ondulata (sempre quella). Sull’asse delle ordinate viene riportata l’accelerazione (quindi la forza, se la moltiplico per la massa m) che la massa m (cioè la scocca) subisce.
Vedete che, in corrispondenza della frequenza di risonanza del mio sistema molla-massa le accelerazioni hanno un picco? Bene: questo significa che in quel caso, sto eccitando la mia massa m (sospesa dalla molla k) con una frequenza che coincide con la “frequenza propria” del mio sistema molla-massa. Sono, cioè, in condizioni di “risonanza”. Quel valore, dove c’è la freccia è un valore che sta nell’intorno di 1,5 Hz. E questo, mi può benissimo capitare su una strada qualunque: basta che affronti le sconnessioni (le ondulazioni) della strada alla velocità “giusta”.
La schematizzazione molla-massa che abbiamo visto fin qui è una semplificazione estrema, serve soprattutto per chiarire le idee. Per esempio, in questa semplificazione abbiamo trascurato che la sospensione è collegata al suolo attraverso la ruota, che ha una sua elasticità (e un suo smorzamento, come vedremo). E anche che il conducente non si siede direttamente sulla scocca (come invece vogliono che succeda molti piloti di formula, che pretendono di appoggiare le natiche direttamente sulla scocca per "sentire" meglio il comportamento della macchina); bensì, tra la scocca e il pilota c'è il sedile, che ha una sua rigidezza ed un suo smorzamento. Per cui, si deve tenere in conto tutto ciò.
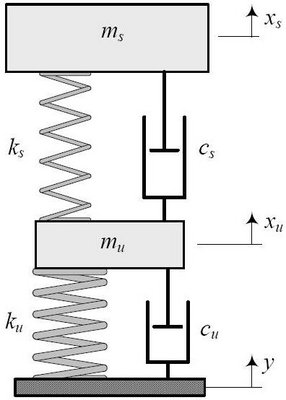
Eccovi, allora, nel disegno qui sotto, come si potrebbe rappresentare il caso in cui volessi descrivere la presenza della cassa e della ruota (massa sospesa e massa NON sospesa):
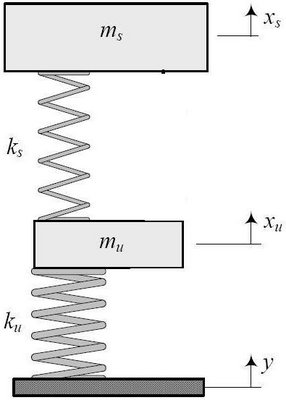
Come potete vedere, i gradi di libertà diventano 2: il grado di libertà della cassa (scocca) e quello che traduce il movimento della ruota (ruota + pneumatico).
Quindi, devo utilizzare DUE equazioni di moto (differenziali del secondo ordine) per descrivere il sistema.
La massa sospesa (cioè SOSPESA dalla sospensione, che sta SOPRA la sospensione) è la cassa (indicata con Ms); la massa NON sospesa (non sospesa dalla sospensione, che sta SOTTO la sospensione) è la ruota, con tutto quello che gli sta attorno (disco, mozzo, ecc).
Volendo precisare, una parte della sospensione va in quota alla massa sospesa e la restante parte alla massa non sospesa.
Torniamo un attimo al sistema molla-massa singola, più semplice da capire.
Dall'equazione differenziale ho ricavato l'equazione del moto:
x(t) = A cos (ωt + φ)
Ve la riscrivo così:
x(t) = Z0 cos (ωt + φ)
In pratica, ho sostituito A con Z0, così posso usare il disegno qui sotto e che mi serve per farvi capire cosa siano Z0 (o, se preferite chiamarlo A, chiamatelo pure A), ω e φ.
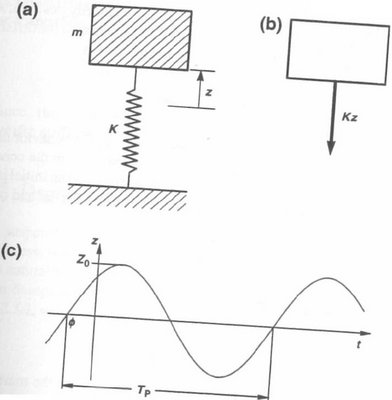
T è il periodo di oscillazione, cioè T = 2 * / ω
La sinusoide disegnata rappresenta il movimento della mia massa che oscilla.
A è l'ampiezza
φ è la fase
ω è, come noto, la frequenza propria.
A e φ dipendono dalle condizioni iniziali del sistema (cioè, da come è partito, da quando ho iniziato a contare).
Avete capito che la sospensione deve garantire il contatto con la strada, l'handling e il confort.
Adesso, ditemi voi come riesce a fare tutto ciò se ha solo le molle, dato che la scocca (il veicolo) è particolarmente propensa a "vibrare" alla sua frequenza naturale (frequenza propria, che come abbiamo detto è oltremodo bassa e facilmente "eccitabile" dalla irregolarità stradale). Con la conseguenza che le grandi oscillazioni della scocca porterebbero a far staccare le ruote da terra.
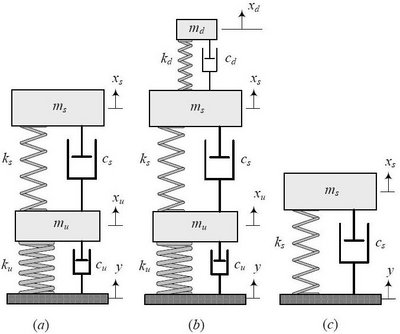
Quindi bisogna ricorrere agli ammortizzatori, e il mio schema si trasforma in quello qui sotto:
E’ chiaro che il disegno che mostrava la massa sospesa (scocca) e quella non sospesa (ruota) collegate SOLO con la molla, adesso diventa come indicato qui sotto.
questo disegno "descrive" perfettamente la ruota (che ha un comportamento elastico e anche smorzante) e la presenza della sospensione dotata di molla e ammortizzatore.
Se poi proprio vogliamo esagerare, e descrivere perfettamente cosa arriva al conducente e ai passeggeri dalla strada, dobbiamo aggiungere anche lo schema che rappresenta il sedile, pure lui dotato di effetto elastico e smorzante.
Quindi avremo la figura successiva.
Come vedete, i gradi di libertà diventano 3 (caso b del disegno)
Se consideriamo 1 solo passeggero su un'auto (che, come noto, dovrebbe essere dotata di 4 ruote e quindi 4 sospensioni), allora devo risolvere 9 equazioni (di secondo grado).
Se devo descrivere il comportamento di 4 passeggeri, allora le equazioni diventano 12 perché diventano 12 i g.d.l.
Direi che le cose incominciano a complicarsi un po', e noi, per semplificare le cose (anche perché NON dobbiamo fare nessun calcolo particolare, ma solo capire le cose), ritorniamo al nostro disegnino, semplice semplice, raffigurato nel caso c, quindi con 1 SOLO grado di libertà.
L'ammortizzatore è un elemento il cui scopo è dissipare l'energia elastica della molla, smorzando l'oscillazione.
L'ammortizzatore genera una forza che si OPPONE al moto della massa (al moto relativo del sistema molla-massa); la forza che genera è PROPORZIONALE alla velocità con cui si muove la sospensione. Più la sospensione si muove velocemente, maggiore (fino a un certo punto) è la forza che genera.
questo significa che, se la sospensione non si muove, l'ammortizzatore NON lavora. Se non c'è movimento, non c'è forza.
Se la sospensione non si muove, la molla genera comunque una forza, perché la forza elastica è funzione solo della posizione, della deformazione, della molla.
Invece, se la sospensione non si muove, l'ammortizzatore NON genera alcuna forza, perché la forza dissipatrice generata dall'ammortizzatore è funzione solo del movimento, della velocità.
Tale forza, dunque, si può esprimere come F = C v dove v è la velocità con cui si muove la sospensione.
Quindi se facciamo riferimento al nostro disegno, la mia v è la derivata rispetto al tempo di x, grado di libertà del mio sistema molla-massa (e ora ammortizzatore).
Quindi: F = C x'
dove con x' ho indicato la derivata di x rispetto a t (dx/dt), cioè v, velocità.
Anzi, per la precisione, dovrei scrivere F = -C x', col meno davanti, perché è una forza che SI OPPONE al moto della sospensione.
il coefficiente C prende il nome di coefficiente di smorzamento dell'ammortizzatore.
Perciò avrò che la mia massa (la scocca) in movimento sarà sottoposta, adesso, a 2 forze: quella elastica (già vista) e quella smorzante (dell'ammortizzatore).
F = - K x + (- C x'), cioè F = - K x - C x'
Ora, in base alla seconda legge di Newton:
m x" = F = - K x - C x'
Ossia:
m x" + C x' + K x = 0
Anche questa è un'equazione differenziale di secondo ordine. Con tutti i coefficienti, tra l'altro, e costanti.
Adesso, se divido tutto per m avrò
x" + (C/m) x' + (K/m) x = 0
K/m dovreste conoscerlo bene: altro non è se non il quadrato di ω, che poi è la pulsazione (la frequenza propria) del mio sistema molla-massa.
Vediamo come si risolve.
Posso scrivere la mia equazione differenziale così:
D2 + C/m D + K/m = 0
Questa diventa una equazione normalissima del secondo ordine.
La soluzione, come noto, è:

Attenti bene:
α, cioè C2/4m2, prende il nome di indice di smorzamento;
ωn che sta sotto la radice è, come noto, la pulsazione (frequenza propria del mio sistema NON smorzato, cioè molla-massa e basta).
Adesso, il problema E’ determinare il valore di quello che sta sotto la radice quadrata.
Infatti, a seconda che il valore che sta sotto la radice quadrata sia:
= 0;
>0;
<0.
Avrò risultati diversi.
Nel primo caso (il valore di ciò che sta sotto la radice quadrata è uguale a 0), avrò 2 (DUE) radici coincidenti;
nel secondo caso, avrò due radici (cioè due soluzioni) reali;
nel terzo caso, avrò due radici complesse.
Naturalmente, per ogni caso qui descritto, il significato fisico è BEN DIVERSO.
1) Partiamo dalla soluzione più semplice, cioè quella in cui tutto quello che sta sotto la radice quadrata è uguale a 0. Questo significa che:
C2/4m2 = K/m ossia:
C = 2 * SQR(k m) ossia 2 per la radice quadrata di (k m)
Questo valore di C (smorzamento dell’ammortizzatore) prende il nome di SMORZAMENTO CRITICO e da adesso lo indicheremo con Cc. Quale sia il suo significato fisico, lo vedremo tra pochissimo. Diciamo subito che quando la frequenza propria, la pulsazione del mio sistema molla-massa-ammo, diventa uguale all’indice di smorzamento, significa che C assume il valore di smorzamento critico (Cc).
2) Adesso, vediamo il caso in cui il valore di quello che sta sotto la radice qudrata è <0.
Chiaro, in questo caso, che sarà:
C < 2 * SQR(k m)
Ossia che lo smorzamento del mio ammortizzatore sarà inferiore al valore di smorzamento critico Cc.
La soluzione, cioè l’equazione del moto del mio sistema al di sotto dello smorzamento critico per il modello totale dell'ammortizzatore e della molla è la seguente:
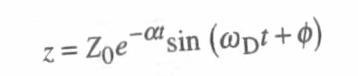
Dove ho indicato con la lettera greca il valore:
= C / Cc cioè = C / 2 * SQR(k m) ma anche = α / ωn
(z greca) prende il nome di COEFFICIENTE DI SMORZAMENTO (o fattore di smorzamento).
Chiaramente, nel caso in cui quello che sta sotto la radice quadrata è <0, il valore di
sarà compreso tra 0 e 1.
E dove ωd, ossia la FREQUENZA PROPRIA (pulsazione) del sistema smorzato (cioè con ammortizzatore), è messo in relazione con la frequenza propria (pulsazione) del sistema non smorzato (il mio sistema molla-massa, senza ammortizzatore) ωn (d sta per “damped” e n sta per “natural”) nel seguente modo:
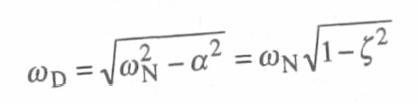
Anche in questo caso, Zo e φ dipendono dalle condizioni iniziali.
3) Ultimo caso, quello in cui il valore di quello che sta sotto la radice quadrata è >0.
Quindi, ho due soluzioni reali.
In questo caso, avrò che:
C > 2 * SQR(k m)
Ossia che lo smorzamento del mio ammortizzatore è superiore allo smorzamento critico e la soluzione dell’equazione differenziale, cioè la mia equazione del moto, diventerà:
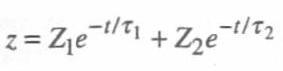
Dove:
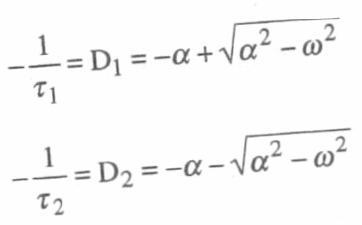
Anche in questo caso, Z1 e Z2 e φ dipendono dalle condizioni iniziali.
Riassumendo il tutto:
La soluzione dell’equazione differenziale dipende dallo smorzamento dell’ammortizzatore:
- Se lo smorzamento è abbastanza piccolo, il sistema vibrerà, ma smetterà di vibrare col tempo. Questo caso (cioè se C < 2 * SQR(k m) ) è detto sistema “sottosmorzato” (questo caso è di particolare interesse nell'analisi delle vibrazioni);
- Se aumentiamo lo smorzamento appena al punto in cui il sistema non oscilla più si raggiungerà il punto di smorzamento critico (C = 2 * SQR(k m) );
- Se lo smorzamento del mio ammortizzatore è aumentato oltre lo smorzamento critico il sistema è denominato “sovrasmorzato”.
Abbiamo visto che vanno tenuto in considerazione 3 parametri fondamentali:
- lo smorzamento dell’ammortizzatore C;
- l’INDICE DI SMORZAMENTO α (= C/2m);
- il COEFFICIENTE (o FATTORE) DI SMORZAMENTO = C / 2 SQR(km).
Attenti bene: spesso trovate che lo smorzamento dell’ammortizzatore C venga chiamato anche “coefficiente di smorzamento dell’ammortizzatore”: non confondetelo con l’altro coefficiente di smorzamento) cioè con lo .
Il comportamento dinamico della (quasi) totalità dei veicoli terrestri ha ammortizzatori i cui coefficienti danno luogo a un sistema SOTTOSMORZATO. Quindi, tenete in conto solo quello.
Confrontiamo la legge oraria del sistema sottosmorzato da quella del sistema SENZA ammortizzatore.
La prima formula è la soluzione, cioè l'equazione del moto, del sistema con ammortizzatore SOTTOSMORZATO.
La seconda è la formula del sistema molla-massa SENZA ammortizzatore.
Che cosa cambia?
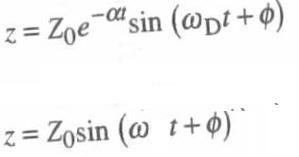
Cambia:
- l'espressione della frequenza propria (la pulsazione), che nel sistema sottosmorzato risulta essere pari alla radice quadrata del quadrato della differenza tra la frequenza (la pulsazione) naturale del sistema senza ammortizzatori e il fattore di smorzamento. quando lo smorzamento raggiunge il valore di smorzamento critico, questa differenza si annulla;
- il termine esponenziale che è quello che fa smorzare l'oscillazione.
Tutto il resto rimane uguale al sistema libero (cioè non smorzato) molla-massa: Z0 e φ dipendono dalle condizioni iniziali.
Osservate il prossimo disegno:
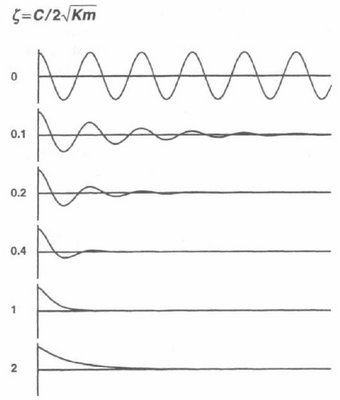
Vengono riportati alcuni grafici al variare del coefficiente di smorzamento.
Quando il coefficiente di smorzamento è uguale a zero, significa che il mio smorzamento C dell'ammortizzatore è uguale a 0, cioè sono senza ammortizzatore, cioè ancora sono nel sistema molla-massa che abbiamo descritto all'inizio. Quindi, ho un'oscillazione libera (che, almeno teoricamente, non finisce mai: continuo a oscillare all'infinito).
Quando il coefficiente di smorzamento è compreso tra 0 e 1 il sistema è in condizioni di SOTTOSMORZAMENTO: la mia oscillazione ha un termine. Quanto più mi avvicino a 1, tanto più la mia oscillazione viene smorzata (frenata) rapidamente. Vedete come varia se passo da un coefficiente di smorzamento di 0,1 a uno di 0,4? Il più rapido e controllato ritorno alle condizioni stabili del mio sistema è tanto maggiore quanto più vicino a 1 mi porto col valore di coefficiente di smorzamento.
il valore di coefficiente di smorzamento uguale a 1 significa che il mio ammortizzatore ha uno smorzamento pari allo SMORZAMENTO CRITICO. Sono cioè in condizioni di smorzamento critico. Se notate, è la prima condizione in cui NON ho overshut.
Un valore di coefficiente di smorzamento maggiore di 1 (esempio, 2 del grafico) mi pone nelle condizioni di SOVRASMORZAMENTO. Questa condizione è utilizzata molto raramente, perché il ritorno alle condizioni di equilibrio è davvero lentissimo (e praticamente inutile).
Veniamo alle auto. Come detto, il valore di coefficiente di smorzamento che mi garantisce il più rapido ritorno alla stabilità e nessun overshut è 1, cioè la condizione di smorzamento critico.
Le macchine che utilizziamo noi, hanno valori di coefficiente di smorzamento di circa 0,3. Le migliori, valori compresi tra 0,3 e 0,6. Le sportive sono sullo 0,6/0,8 (o anche oltre), le macchine da corsa hanno valori che si approssimano a 1.
E’ chiaro che il miglior handling si ottiene per valori di 1, ma come al solito bisogna fare i conti col confort.
Una macchina con gli ammortizzatori scoppiati ha valori di coefficiente di smorzamento nell'ordine dello 0,3-0,1.
Struttura di un ammortizzatore.
Prima di andare avanti a discutere sul coefficiente di smorzamento (c) dell’ammortizzatore, facciamo una sosta per vedere come è fatto un ammortizzatore, perché questo ci servirà per capire il seguito.
Eccovi dunque un disegno di un ammortizzatore come lo conoscete, cioè quello di una sospensione McPherson.
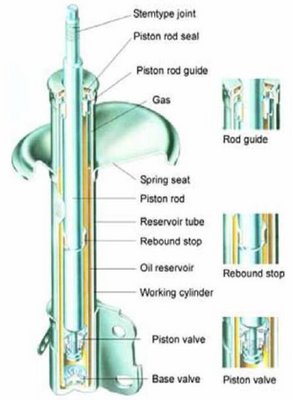
In realtà, esisterebbero moltissimi schemi (tipi) di ammortizzatori. Per esempio, le balestre svolgono la funzione di molle e quella di ammortizzatori, perché l’attrito tra le foglie delle balestre smorza le oscillazioni (infatti, le vetture a balestre sono particolarmente sconfortevoli, seppure robuste). Altro esempio, che sfrutta sempre lo stesso principio (attrito dovuto al movimento relativo, lo strisciamento, tra due corpi), quegli ammortizzatori composti da due “lame” infulcrate tra loro all’estremità e sporgenti rispetto all’asse ruote, che potete notare su molte auto anteguerra.
Noi, però, per semplicità, ci dedicheremo agli ammortizzatori idraulici telescopici.
Anche in questo caso, ci sono molte variazioni sul tema: classificazioni varie, etc. Diciamo che la classificazione principale riguarda il metodo secondo il quale si “dispone”, come varia, il volume di olio rispetto al pistone che scorre nel cilindro; e questo è un gran bel problema, perché l’olio è un fluido molto poco comprimibile e se devo garantire all’ammortizzatore una lunga corsa dello stelo, le cose si complicano un po’ (dove metto l’olio che sposto?).
Comunque, guardate la figura successiva:
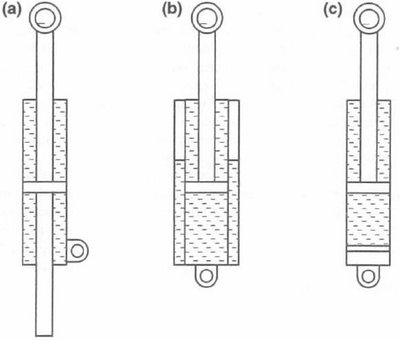
Di base, ci sono tre tipi di ammortizzatore (telescopici idraulici):
a) telescopici con il fluido che passa tra le due camere
b) telescopici “bitubo”
c) telescopici a tubo singolo
Quelli di tipo a) risolvono il problema dello spostamento del fluido semplicemente spostandolo al di sopra e al di sotto del pistone. Questa soluzione ha indubbi vantaggi nell’ottimizzazione dello spazio (occupa poco spazio e posso collocarlo dove voglio) ma presenta lo svantaggio di sollecitare molto le guarnizioni di tenuta alle estremità del cilindro che contiene l’olio (che sono sottoposte ad elevate pressioni, col rischio di perdite di tenuta). Inoltre, quando lo stelo raggiunge la sua corsa massima, c’è l’elevato rischio di inconvenienti o danneggiamenti delle estremità e, infine, si deve tenere in qualche conto del fatto che l’olio, che si riscalda durante il funzionamento dell’ammortizzatore, varia anche di volume. Diciamo che, per le sospensioni, non va bene; al contrario, è molto usato come ammortizzatore di sterzo (è messo sugli sterzi).
Il tipo b) (bitubo) presenta due tubi coassiali: il cilindro esterno contiene del gas (comprimibile) che compensa la variazione di volume del cilindro durante lo scorrimento del pistone e il conseguente spostamento dell’olio. Questo è, generalmente, il tipo più usato nelle sospensioni.
Il gas c’è anche nel tipo c) (monotubo) e, generalmente, questo è emulsionato con l’olio; in alcuni casi, il gas è invece separato dall’olio da un ulteriore pistone (o una membrana robusta) che evita, appunto l’emulsione. Se guardate la figura c) vedrete questo setto di separazione. Questo particolare tipo di ammortizzatore monotubo è del tipo De Carbon (dal nome del suo inventore).
Vediamo ora da quali elementi è costituito un ammortizzatore e come funziona.
Consideriamo, per semplicità, un ammortizzatore idraulico monotubo. Ma i principi di funzionamento vanno bene anche per tutti gli altri tipi di ammortizzatori idraulici e idropneumatici (come ad es. i bitubo, gli idropneumatici, quelli ad alta e bassa pressione etc).
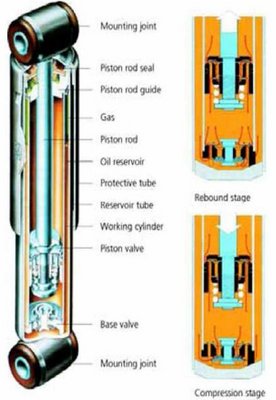
Osservate la figura successiva.
All’interno del cilindro, chiuso ad una estremità, scorre uno stantuffo (un pistone) solidale con uno stelo. Il cilindro da una parte e lo stelo, dall’altra, sono collegati l’uno alla sospensione e l’altro alla scocca.
Il tubo è riempito con l’olio; che in realtà proprio olio non è, ma è un fluido speciale che deve avere come caratteristica la capacità di mantenere la viscosità il più possibile stabile al variare della temperatura (che poi, anche qui, non si possono certo fare miracoli: provate a lasciare la macchina parcheggiata all’aperto una notte in montagna d’inverno. E poi, alla mattina, mettetevi in auto e partite: anche la più confortevole delle vetture, appena partite, vi sembrerà rigida come un carretto. Semplicemente perché gli ammortizzatori sono freddi; e freddo, denso e viscoso, sarà pure il fluido all’interno…).
Comunque, questo fluido trafila, durante il movimento del pistone, attraverso dei fori calibrati (delle valvole) ricavati sul pistone stesso. In funzione di come sono “calibrate” le valvole, ossia della loro sezione di passaggio attraverso cui scorre il fluido, si riesce a dare all’ammortizzatore la caratteristica (cioè la frenatura, ossia il coefficiente di smorzamento) che si vuole.
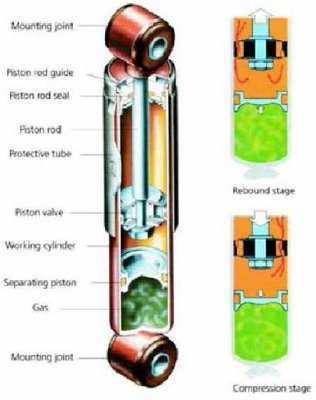
Del tutto simile al monotubo è il bitubo, costituito da 2 cilindri coassiali: uno di “lavoro”, dove scorre il pistone; l’altro di “riserva” dove finisce il fluido spostato dal pistone durante il movimento.
Poi, ci sarebbero anche gli ammortizzatori con il serbatoio del fluido separato ed esterno (tipo gli Ohlins da moto, tanto per citarne alcuni).
Le valvole di controllo, poste sul pistone e alla base della camera di “lavoro” (nel caso dell’ammortizzatore bitubo) sono un sistema composto da rondelle di spinta, molle a spirale e veri e propri corpi valvola accuratamente tarati.
Abbiamo chiarito come sono fatti gli ammortizzatori idraulici che, lo ripeto, sono ben diversi dagli ammortizzatori a frizione (come le balestre). È importante che capiate che sono differenti, perché adesso vedremo IN COSA lo sono (nel senso che uno potrebbe anche dire: e allora, perché non metto un ammortizzatore a frizione e la finiamo lì?).
Prima però, mi interessa che capiate bene un paio di concetti.
1) Attenti a non confondere le molle con gli ammortizzatori. Le prime lavorano “in dinamica e in statica”. Gli altri lavorano solo “in dinamica”. Deve essere chiaro. Insomma, se tolgo le molle e tengo solo gli ammortizzatori, la macchina si siede, si abbassa FINO AI TAMPONI. E se questi non ci sono, arrivo alla fine della compressione della sospensione e lì rimango. Punto. La macchina senza molle non funziona. Al limite, invece, potrei andare con solo le molle (salvo rimbalzare fuoristrada alla prima curva): la macchina mantiene il suo assetto statico e, ammettendo di rollare, beccheggiare, frenare, accelerare, girare il volante, etc in un tempo INFINITO (quindi, attraverso infiniti istanti di “transitorio esaurito”), riuscirei ad andare… Peccato che la realtà NON sia questa. Quindi, molle e ammortizzatori si completano a vicenda.
La forza esercitata dalla molla è funzione della posizione x (estensione e/o compressione) a meno di un coefficiente di proporzionalità.
La forza espressa dall’ammortizzatore è SOLO funzione della velocità (v, o x’) con cui si muove il pistone (lo stelo) rispetto al cilindro (tubo che contiene l’olio).
2) Nel sistema schematico molla – massa - ammortizzatore, non è ben chiaro COSA sia la massa, cioè QUANTO vale.
In precedenza, per fissare i concetti di base, avevamo detto che la massa M era la massa (la porzione di massa) sospesa. Invece, a differenza della molla e dell’ammortizzatore, che sono facilmente riconducibili agli elementi che costituiscono la sospensione, la massa M può essere intesa, alternativamente, come la massa sospesa o la massa NON sospesa.
Mi spiego meglio: supponiamo di stare percorrendo una strada ondulata. La scocca si muove rispetto alle ruote, che seguono il profilo stradale. In questo caso, è la scocca che si muove, quindi ricadiamo nel primo caso: massa SOSPESA che si muove. E quindi la mia M è la massa sospesa (o quella porzione di massa sospesa che compete alla sospensione che sto considerando).
Invece, se affronto un gradino, o una buca , e la ruota si stacca dal terreno, quindi si muove rispetto alla scocca, che massa considero? La massa NON sospesa, perché è la ruota.
Bene: mi sembra chiaro che le masse sono MOLTO differenti. Ruota e scocca hanno masse MOLTO differenti, inerzie MOLTO differenti; ma anche velocità MOLTO differenti….per cui l’ammortizzatore dovrà fornire differenti forze di smorzamento. Ossia, differente dovrà essere la forza di smorzamento che l’ammortizzatore fornisce durante i due movimenti (che possono accadere; anzi, è normalissimo che accadano quando si viaggia).
Allora, come possiamo fare? Semplice, adottando due differenti tipi di valvole.
Il fatto è che ad un ammortizzatore si richiede che abbia almeno due caratteristiche differenti di smorzamento: una, modesta, per smorzare i moti della cassa (la massa sospesa), che sono lenti; un’altra, più energica, più forte, per smorzare i moti delle ruote (masse NON sospese), che sono più veloci.
Prima di vedere come sia la caratteristica di un ammortizzatore, vediamo come si realizza questa condizione. Sulla base della considerazione 2): con le valvole. Cioè, le differenti caratteristiche, quella modesta per smorzare i moti lenti delle masse sospese e quella forte per i moti delle masse non sospese, si ottengono con i fori calibrati.
Una serie di fori piccoli e SEMPRE APERTI frenano i moti lenti, perché consentono il passaggio continuo del fluido tra le due camere che il pistone crea all’interno del cilindro di lavoro.
Un’altra serie di fori grandi, ma dotati di valvole di chiusura opportunamente tarate, frenano i moti rapidi delle ruote. Le valvole si aprono automaticamente al raggiungimento di una soglia di pressione e di una quantità tanto più grande quanto maggiore è la pressione che il fluido esercita su di esse durante i moti veloci delle ruote. Sono, insomma, delle valvole PROPORZIONALI (normalmente chiuse). Ora, visto che la pressione che il liquido esercita sulle valvole è funzione diretta della velocità del pistone (e quindi dello stelo dell’ammortizzatore), quanto più veloce andrà lo stelo, cioè in definitiva la ruota, tanto maggiore sarà la forza che “frena” la ruota nel suo movimento (verticale).
È chiaro che, se non ci fossero queste valvole calibrate, in corrispondenza dei fori di grosso diametro, a regolare la forza che contrasta il moto delle masse non sospese e ci affidassimo solo ai fori calibrati di piccolo diametro (che gestiscono i moti lenti delle masse sospese), le resistenze idrauliche (le perdite di carico) generate dal fluido nel passaggio per questi fori sarebbero talmente elevate da rendere, di fatto, l’ammortizzatore troppo “duro” (passatemi il termine scorretto, ma è per farvi capire); troppo frenato, troppo “rigido”.
Al contrario, l’assenza delle valvole calibrate nei fori grandi lascerebbe troppo “libero” l’ammortizzatore nei moti lenti della scocca (masse sospese), rendendo l’ammortizzatore troppo “morbido”. E la mia BMW diventerebbe una Citroen…
Infatti, le valvole restano chiuse nei moti lenti (basse velocità dello stelo, e quindi del fluido) e obbligano il fluido a passare per i fori piccoli. Oltre un certo valore di ΔP, cioè di differenza di pressione tra le due facce del pistone (tra le due camere di lavoro del cilindro), le valvole si aprono IN PROPORZIONE ALLA PRESSIONE (e quindi alla velocità dello stelo)…
Va considerato perciò che l’ammortizzatore NON lavora solo in un senso, per esempio solo in compressione, ma anche in estensione. Ossia, lavora sia quando la sospensione si comprime (a tamponamento), sia quando si estende (a rimbalzo). Ora, il fatto che l’ammortizzatore lavori nei due sensi, lo qualifica come ammortizzatore A DOPPIO EFFETTO.
Questa caratteristica lo distingue dagli ammortizzatori più semplici detti A SEMPICE EFFETTO perché agiscono (lavorano) solo in un senso.
Allora, possiamo andare a vedere le curve caratteristiche che appunto descrivono il funzionamento dell’ammortizzatore.
:grazie) alfistavero
Per parlare degli ammortizzatori, occorre conoscere un pochino le derivate di secondo ordine. Chi le conosce, va tranquillo; chi non le conosce, avrà qualche difficoltà in più. Comunque, vedremo di fare le cose semplici semplici, tirandole in ballo solo per il tempo necessario e non oltre.
Finora abbiamo visto la nostra macchina appoggiata sulle sospensioni dotate di molle. Diciamo che, se conosciamo (e possiamo conoscerla) la massa che grava sulla singola sospensione, possiamo schematizzare il tutto come nel disegno qui sotto:

m è la massa sospesa su ciascuna singola sospensione.
Poi c'è la molla, di costante elastica K.
Chiaramente, questo è uno schema semplicissimo, perché ho trascurato tante altre "variabili": per esempio, ho tralasciato il pneumatico, che si comporta anch'esso come una molla (e come un ammortizzatore).
Ad ogni modo, questo è lo schema che descrive, abbastanza bene, il lavoro della mia sospensione (dal punto di vista energetico).
Se la strada mi fa comprimere o estendere la molla, la mia molla si comprime o si estende: quindi, si genera una forza.
Come potete anche vedere, questo è un sistema con 1 grado di libertà (andate a ri-vedervi il discorso delle coordinate libere, dei gradi di libertà e dei gradi di vincolo fatto nella prima Faq sulle sospensioni): la coordinata libera è la mia X: la massa può muoversi solo in verticale.
Quindi, X è lo spostamento. Quello che nel disegno è indicato con X col puntino sopra è la derivata di X rispetto al tempo (dX/dt), cioè la velocità con cui si muove la mia massa all'istante in cui la osservo.
Se guardo la massa a destra, nel disegno sopra, vedo che questa è spostata di una certa quantità (x) rispetto alla posizione indeformata. Questo significa che la mia massa m si sta muovendo rispetto alla posizione di equilibrio (per esempio, perché ho preso una buca, o una sconnessione della strada). Quindi, significa anche che la mia molla, che in condizioni di equilibrio era compressa di una certa quantità per generare una forza che sostenesse il peso della massa m, sta generando una forza F proporzionale alla sua elongazione x. Cioè, F = k x.
Se applico la legge di Newton che recita F = m a (per essere precisi, va però detto che NON ha scritto la sua famosa legge nella forma F = m a , bensì nella forma F = dQ/dt, ossia derivata della quantità di moto rispetto al tempo. Ora, siccome la quantità di moto Q vale Q = m v, la formula di Newton diventa F = m (dv/dt) + v (dm/dt). Noi supponiamo, con buona approssimazione, che la massa m non cambi, per cui il mio termine dm/dt è uguale a 0. Quindi, rimane solo che F = m (dv/dt) cioè F = m a) avrò:
F = k x (anzi a –k x perché la forza elastica si oppone al moto della massa m)
mentre m a diventa m (dv/dt) = m (d2x/dt2) = m x” (con x” ho indicato la derivata seconda dello spostamento).
Quindi:
m x” – k x = 0
cioè x” – (k/m) x = 0
Ora, se pongo ω2 = k/m
riscrivo il tutto come x” - ω2 x = 0
Questa è la legge di moto che descrive, appunto, il movimento della mia massa m sostenuta dalla molla. Ma questa è anche un’equazione differenziale (a coeff. costanti) del secondo ordine.
L’integrale (cioè la soluzione) di questa equazione è:
x(t) = A cos (ωt + φ)
che è l’equazione di un moto armonico.
A e φ sono due coefficienti che dipendono dalle condizioni iniziali del sistema (es. da quando comincio a misurare, etc).
Quello che importa, invece, è il valore ω, che prende il nome di frequenza propria del sistema
e vale, appunto, ω = sqrt (k/m) (ossia radice quadrata di k/m).
Guardiamo l’equazione di moto del sistema molla-massa:
x(t) = A cos (ωt + φ)
Tralasciamo i valori A e φ per il momento.
Concentriamoci sulla frequenza propria, cioè su ω.
Questa vale, come detto SQR(k/m), ossia radice quadrata di k/m, dove:
k è la costante elastica della molla;
m è la massa (della mia porzione di macchina);
ω è dunque la frequenza propria del sistema e si misura in Hertz (Hz).
Chiaro, a questo punto, che io possa determinare anche il periodo di oscillazione, ossia il tempo che intercorre tra due istanti uguali della mia oscillazione. Il periodo è T = 2 / ω
ossia T = 2 * (PIgreco) / SQR(k/m)
Cosa significa tutto ciò?
Che la mia macchina, schematizzata come una massa m su molla k, se sottoposta ad un’azione perturbatrice (irregolarità del terreno), incomincerà ad oscillare. Oscillerà con una certa frequenza, che dipende dalla massa della macchina e dalla rigidezza della molla.
L’accelerazione che subirà la mia massa, cioè la mia scocca (o la parte di scocca di massa m con cui ho schematizzato la macchina) dipenderà dalla frequenza dell’eccitazione dovuta alla strada. Ossia, se la mia strada ha una certa ondulazione e io la percorro avanti e indietro a velocità crescenti, la mia scocca (la massa m) comincerà ad oscillare sempre più. Data la strada e la sua ondulazione, posso modificare la frequenza con cui “eccito” la scocca semplicemente percorrendo la strada a velocità differenti. Provate a pensarci. Supponiamo che cominci a bassissima velocità. La mia scocca inizia ad oscillare piano. Poi aumento un po’ la velocità e la scocca oscilla sempre un po’ di più. La mia scocca sarà sottoposta ad accelerazioni sempre maggiori perché la mia eccitante (la strada ondulata) “eccita”, appunto, sempre più la scocca.
Ad un certo punto, arriverò a percorrere la strada ondulata ad una velocità tale che la frequenza delle mie oscillazioni eccitanti coincidono con la frequenza propria della mia macchina ω = SQR(k/m). In questo caso, l’accelerazione della scocca (cioè della mia massa m) diventerà elevatissima: questo significa che la strada, percorsa a quella determinata velocità, ha eccitato la frequenza propria della mia macchina. Cioè l’eccitante (la strada) ha frequenza pari alla frequenza propria del mio sistema (sistema molla-massa).
Chiaramente, se a quella velocità avessi una macchina diversa (cioè con m diversa) o mettessi una molla diversa (ossia con un diverso k), la mia frequenza propria sarebbe differente (maggiore o minore di prima) e quindi manderei “in risonanza” la macchina ad una velocità differente (maggiore o minore) su quella determinata strada. Precisamente, se aumento la rigidezza k della molla, la mia frequenza aumenterà (k è al numeratore); se aumento m, la mia frequenza diminuirà (m è al denominatore). Se diminuisco l’una o l’altra, succederà il contrario. se modifico l’una E l’altra, dipende dall’entità delle due modifiche.
Questo è quello che succede se viaggio con una macchina dotata solamente di molle (senza ammortizzatori). In pratica, la mia scocca continuerà ad oscillare e, facilmente, mi troverò in condizioni di “risonanza”. E guardate che è abbastanza facile trovarsi in quelle condizioni, perché la frequenza propria della cassa, della scocca, è piuttosto bassa, nell’ordine dell’1,5 Hz. Avete capito bene: 1,5 Hz (la ruota – cerchio + pneumatico - ha invece una frequenza propria di un ordine di grandezza maggiore, quindi siamo nell'ordine dei 15 Hz).
Se proprio vogliamo esagerare e comprendere tutti i tipi di scocca, diciamo che la frequenza propria di una scocca varia tra 1 e 2 Hz (proprio a voler stare larghi). Le frequenza maggiori sono proprie delle vetture con scocca più rigida.
E se mi trovo in condizioni di risonanza, significa che “spicco il volo” con la scocca. Ossia, la mia scocca (e tutto quello che c’è dentro) subirà delle accelerazioni molto elevate.
Per farvi capire meglio il problema, allego il grafico seguente.
Sull’asse delle ascisse c’è la frequenza delle mie forze perturbatrici (eccitanti). Affinché comprendiate meglio, fate finta che su quell’asse ci sia la velocità con cui percorrete la strada ondulata (sempre quella). Sull’asse delle ordinate viene riportata l’accelerazione (quindi la forza, se la moltiplico per la massa m) che la massa m (cioè la scocca) subisce.
Vedete che, in corrispondenza della frequenza di risonanza del mio sistema molla-massa le accelerazioni hanno un picco? Bene: questo significa che in quel caso, sto eccitando la mia massa m (sospesa dalla molla k) con una frequenza che coincide con la “frequenza propria” del mio sistema molla-massa. Sono, cioè, in condizioni di “risonanza”. Quel valore, dove c’è la freccia è un valore che sta nell’intorno di 1,5 Hz. E questo, mi può benissimo capitare su una strada qualunque: basta che affronti le sconnessioni (le ondulazioni) della strada alla velocità “giusta”.

La schematizzazione molla-massa che abbiamo visto fin qui è una semplificazione estrema, serve soprattutto per chiarire le idee. Per esempio, in questa semplificazione abbiamo trascurato che la sospensione è collegata al suolo attraverso la ruota, che ha una sua elasticità (e un suo smorzamento, come vedremo). E anche che il conducente non si siede direttamente sulla scocca (come invece vogliono che succeda molti piloti di formula, che pretendono di appoggiare le natiche direttamente sulla scocca per "sentire" meglio il comportamento della macchina); bensì, tra la scocca e il pilota c'è il sedile, che ha una sua rigidezza ed un suo smorzamento. Per cui, si deve tenere in conto tutto ciò.
Eccovi, allora, nel disegno qui sotto, come si potrebbe rappresentare il caso in cui volessi descrivere la presenza della cassa e della ruota (massa sospesa e massa NON sospesa):

Come potete vedere, i gradi di libertà diventano 2: il grado di libertà della cassa (scocca) e quello che traduce il movimento della ruota (ruota + pneumatico).
Quindi, devo utilizzare DUE equazioni di moto (differenziali del secondo ordine) per descrivere il sistema.
La massa sospesa (cioè SOSPESA dalla sospensione, che sta SOPRA la sospensione) è la cassa (indicata con Ms); la massa NON sospesa (non sospesa dalla sospensione, che sta SOTTO la sospensione) è la ruota, con tutto quello che gli sta attorno (disco, mozzo, ecc).
Volendo precisare, una parte della sospensione va in quota alla massa sospesa e la restante parte alla massa non sospesa.
Torniamo un attimo al sistema molla-massa singola, più semplice da capire.
Dall'equazione differenziale ho ricavato l'equazione del moto:
x(t) = A cos (ωt + φ)
Ve la riscrivo così:
x(t) = Z0 cos (ωt + φ)
In pratica, ho sostituito A con Z0, così posso usare il disegno qui sotto e che mi serve per farvi capire cosa siano Z0 (o, se preferite chiamarlo A, chiamatelo pure A), ω e φ.

T è il periodo di oscillazione, cioè T = 2 * / ω
La sinusoide disegnata rappresenta il movimento della mia massa che oscilla.
A è l'ampiezza
φ è la fase
ω è, come noto, la frequenza propria.
A e φ dipendono dalle condizioni iniziali del sistema (cioè, da come è partito, da quando ho iniziato a contare).
Avete capito che la sospensione deve garantire il contatto con la strada, l'handling e il confort.
Adesso, ditemi voi come riesce a fare tutto ciò se ha solo le molle, dato che la scocca (il veicolo) è particolarmente propensa a "vibrare" alla sua frequenza naturale (frequenza propria, che come abbiamo detto è oltremodo bassa e facilmente "eccitabile" dalla irregolarità stradale). Con la conseguenza che le grandi oscillazioni della scocca porterebbero a far staccare le ruote da terra.
Quindi bisogna ricorrere agli ammortizzatori, e il mio schema si trasforma in quello qui sotto:

E’ chiaro che il disegno che mostrava la massa sospesa (scocca) e quella non sospesa (ruota) collegate SOLO con la molla, adesso diventa come indicato qui sotto.
questo disegno "descrive" perfettamente la ruota (che ha un comportamento elastico e anche smorzante) e la presenza della sospensione dotata di molla e ammortizzatore.

Se poi proprio vogliamo esagerare, e descrivere perfettamente cosa arriva al conducente e ai passeggeri dalla strada, dobbiamo aggiungere anche lo schema che rappresenta il sedile, pure lui dotato di effetto elastico e smorzante.
Quindi avremo la figura successiva.
Come vedete, i gradi di libertà diventano 3 (caso b del disegno)
Se consideriamo 1 solo passeggero su un'auto (che, come noto, dovrebbe essere dotata di 4 ruote e quindi 4 sospensioni), allora devo risolvere 9 equazioni (di secondo grado).
Se devo descrivere il comportamento di 4 passeggeri, allora le equazioni diventano 12 perché diventano 12 i g.d.l.
Direi che le cose incominciano a complicarsi un po', e noi, per semplificare le cose (anche perché NON dobbiamo fare nessun calcolo particolare, ma solo capire le cose), ritorniamo al nostro disegnino, semplice semplice, raffigurato nel caso c, quindi con 1 SOLO grado di libertà.

L'ammortizzatore è un elemento il cui scopo è dissipare l'energia elastica della molla, smorzando l'oscillazione.
L'ammortizzatore genera una forza che si OPPONE al moto della massa (al moto relativo del sistema molla-massa); la forza che genera è PROPORZIONALE alla velocità con cui si muove la sospensione. Più la sospensione si muove velocemente, maggiore (fino a un certo punto) è la forza che genera.
questo significa che, se la sospensione non si muove, l'ammortizzatore NON lavora. Se non c'è movimento, non c'è forza.
Se la sospensione non si muove, la molla genera comunque una forza, perché la forza elastica è funzione solo della posizione, della deformazione, della molla.
Invece, se la sospensione non si muove, l'ammortizzatore NON genera alcuna forza, perché la forza dissipatrice generata dall'ammortizzatore è funzione solo del movimento, della velocità.
Tale forza, dunque, si può esprimere come F = C v dove v è la velocità con cui si muove la sospensione.
Quindi se facciamo riferimento al nostro disegno, la mia v è la derivata rispetto al tempo di x, grado di libertà del mio sistema molla-massa (e ora ammortizzatore).
Quindi: F = C x'
dove con x' ho indicato la derivata di x rispetto a t (dx/dt), cioè v, velocità.
Anzi, per la precisione, dovrei scrivere F = -C x', col meno davanti, perché è una forza che SI OPPONE al moto della sospensione.
il coefficiente C prende il nome di coefficiente di smorzamento dell'ammortizzatore.
Perciò avrò che la mia massa (la scocca) in movimento sarà sottoposta, adesso, a 2 forze: quella elastica (già vista) e quella smorzante (dell'ammortizzatore).
F = - K x + (- C x'), cioè F = - K x - C x'
Ora, in base alla seconda legge di Newton:
m x" = F = - K x - C x'
Ossia:
m x" + C x' + K x = 0
Anche questa è un'equazione differenziale di secondo ordine. Con tutti i coefficienti, tra l'altro, e costanti.
Adesso, se divido tutto per m avrò
x" + (C/m) x' + (K/m) x = 0
K/m dovreste conoscerlo bene: altro non è se non il quadrato di ω, che poi è la pulsazione (la frequenza propria) del mio sistema molla-massa.
Vediamo come si risolve.
Posso scrivere la mia equazione differenziale così:
D2 + C/m D + K/m = 0
Questa diventa una equazione normalissima del secondo ordine.
La soluzione, come noto, è:

Attenti bene:
α, cioè C2/4m2, prende il nome di indice di smorzamento;
ωn che sta sotto la radice è, come noto, la pulsazione (frequenza propria del mio sistema NON smorzato, cioè molla-massa e basta).
Adesso, il problema E’ determinare il valore di quello che sta sotto la radice quadrata.
Infatti, a seconda che il valore che sta sotto la radice quadrata sia:
= 0;
>0;
<0.
Avrò risultati diversi.
Nel primo caso (il valore di ciò che sta sotto la radice quadrata è uguale a 0), avrò 2 (DUE) radici coincidenti;
nel secondo caso, avrò due radici (cioè due soluzioni) reali;
nel terzo caso, avrò due radici complesse.
Naturalmente, per ogni caso qui descritto, il significato fisico è BEN DIVERSO.
1) Partiamo dalla soluzione più semplice, cioè quella in cui tutto quello che sta sotto la radice quadrata è uguale a 0. Questo significa che:
C2/4m2 = K/m ossia:
C = 2 * SQR(k m) ossia 2 per la radice quadrata di (k m)
Questo valore di C (smorzamento dell’ammortizzatore) prende il nome di SMORZAMENTO CRITICO e da adesso lo indicheremo con Cc. Quale sia il suo significato fisico, lo vedremo tra pochissimo. Diciamo subito che quando la frequenza propria, la pulsazione del mio sistema molla-massa-ammo, diventa uguale all’indice di smorzamento, significa che C assume il valore di smorzamento critico (Cc).
2) Adesso, vediamo il caso in cui il valore di quello che sta sotto la radice qudrata è <0.
Chiaro, in questo caso, che sarà:
C < 2 * SQR(k m)
Ossia che lo smorzamento del mio ammortizzatore sarà inferiore al valore di smorzamento critico Cc.
La soluzione, cioè l’equazione del moto del mio sistema al di sotto dello smorzamento critico per il modello totale dell'ammortizzatore e della molla è la seguente:
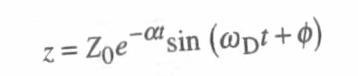
Dove ho indicato con la lettera greca il valore:
= C / Cc cioè = C / 2 * SQR(k m) ma anche = α / ωn
(z greca) prende il nome di COEFFICIENTE DI SMORZAMENTO (o fattore di smorzamento).
Chiaramente, nel caso in cui quello che sta sotto la radice quadrata è <0, il valore di
sarà compreso tra 0 e 1.
E dove ωd, ossia la FREQUENZA PROPRIA (pulsazione) del sistema smorzato (cioè con ammortizzatore), è messo in relazione con la frequenza propria (pulsazione) del sistema non smorzato (il mio sistema molla-massa, senza ammortizzatore) ωn (d sta per “damped” e n sta per “natural”) nel seguente modo:
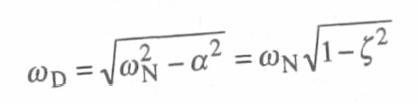
Anche in questo caso, Zo e φ dipendono dalle condizioni iniziali.
3) Ultimo caso, quello in cui il valore di quello che sta sotto la radice quadrata è >0.
Quindi, ho due soluzioni reali.
In questo caso, avrò che:
C > 2 * SQR(k m)
Ossia che lo smorzamento del mio ammortizzatore è superiore allo smorzamento critico e la soluzione dell’equazione differenziale, cioè la mia equazione del moto, diventerà:
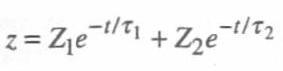
Dove:
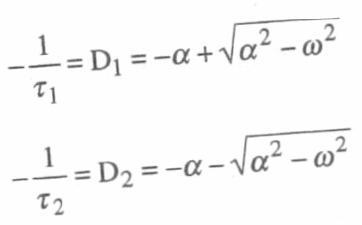
Anche in questo caso, Z1 e Z2 e φ dipendono dalle condizioni iniziali.
Riassumendo il tutto:
La soluzione dell’equazione differenziale dipende dallo smorzamento dell’ammortizzatore:
- Se lo smorzamento è abbastanza piccolo, il sistema vibrerà, ma smetterà di vibrare col tempo. Questo caso (cioè se C < 2 * SQR(k m) ) è detto sistema “sottosmorzato” (questo caso è di particolare interesse nell'analisi delle vibrazioni);
- Se aumentiamo lo smorzamento appena al punto in cui il sistema non oscilla più si raggiungerà il punto di smorzamento critico (C = 2 * SQR(k m) );
- Se lo smorzamento del mio ammortizzatore è aumentato oltre lo smorzamento critico il sistema è denominato “sovrasmorzato”.
Abbiamo visto che vanno tenuto in considerazione 3 parametri fondamentali:
- lo smorzamento dell’ammortizzatore C;
- l’INDICE DI SMORZAMENTO α (= C/2m);
- il COEFFICIENTE (o FATTORE) DI SMORZAMENTO = C / 2 SQR(km).
Attenti bene: spesso trovate che lo smorzamento dell’ammortizzatore C venga chiamato anche “coefficiente di smorzamento dell’ammortizzatore”: non confondetelo con l’altro coefficiente di smorzamento) cioè con lo .
Il comportamento dinamico della (quasi) totalità dei veicoli terrestri ha ammortizzatori i cui coefficienti danno luogo a un sistema SOTTOSMORZATO. Quindi, tenete in conto solo quello.
Confrontiamo la legge oraria del sistema sottosmorzato da quella del sistema SENZA ammortizzatore.
La prima formula è la soluzione, cioè l'equazione del moto, del sistema con ammortizzatore SOTTOSMORZATO.
La seconda è la formula del sistema molla-massa SENZA ammortizzatore.
Che cosa cambia?
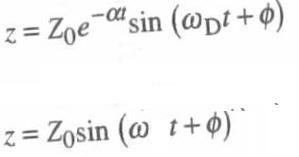
Cambia:
- l'espressione della frequenza propria (la pulsazione), che nel sistema sottosmorzato risulta essere pari alla radice quadrata del quadrato della differenza tra la frequenza (la pulsazione) naturale del sistema senza ammortizzatori e il fattore di smorzamento. quando lo smorzamento raggiunge il valore di smorzamento critico, questa differenza si annulla;
- il termine esponenziale che è quello che fa smorzare l'oscillazione.
Tutto il resto rimane uguale al sistema libero (cioè non smorzato) molla-massa: Z0 e φ dipendono dalle condizioni iniziali.
Osservate il prossimo disegno:

Vengono riportati alcuni grafici al variare del coefficiente di smorzamento.
Quando il coefficiente di smorzamento è uguale a zero, significa che il mio smorzamento C dell'ammortizzatore è uguale a 0, cioè sono senza ammortizzatore, cioè ancora sono nel sistema molla-massa che abbiamo descritto all'inizio. Quindi, ho un'oscillazione libera (che, almeno teoricamente, non finisce mai: continuo a oscillare all'infinito).
Quando il coefficiente di smorzamento è compreso tra 0 e 1 il sistema è in condizioni di SOTTOSMORZAMENTO: la mia oscillazione ha un termine. Quanto più mi avvicino a 1, tanto più la mia oscillazione viene smorzata (frenata) rapidamente. Vedete come varia se passo da un coefficiente di smorzamento di 0,1 a uno di 0,4? Il più rapido e controllato ritorno alle condizioni stabili del mio sistema è tanto maggiore quanto più vicino a 1 mi porto col valore di coefficiente di smorzamento.
il valore di coefficiente di smorzamento uguale a 1 significa che il mio ammortizzatore ha uno smorzamento pari allo SMORZAMENTO CRITICO. Sono cioè in condizioni di smorzamento critico. Se notate, è la prima condizione in cui NON ho overshut.
Un valore di coefficiente di smorzamento maggiore di 1 (esempio, 2 del grafico) mi pone nelle condizioni di SOVRASMORZAMENTO. Questa condizione è utilizzata molto raramente, perché il ritorno alle condizioni di equilibrio è davvero lentissimo (e praticamente inutile).
Veniamo alle auto. Come detto, il valore di coefficiente di smorzamento che mi garantisce il più rapido ritorno alla stabilità e nessun overshut è 1, cioè la condizione di smorzamento critico.
Le macchine che utilizziamo noi, hanno valori di coefficiente di smorzamento di circa 0,3. Le migliori, valori compresi tra 0,3 e 0,6. Le sportive sono sullo 0,6/0,8 (o anche oltre), le macchine da corsa hanno valori che si approssimano a 1.
E’ chiaro che il miglior handling si ottiene per valori di 1, ma come al solito bisogna fare i conti col confort.
Una macchina con gli ammortizzatori scoppiati ha valori di coefficiente di smorzamento nell'ordine dello 0,3-0,1.
Struttura di un ammortizzatore.
Prima di andare avanti a discutere sul coefficiente di smorzamento (c) dell’ammortizzatore, facciamo una sosta per vedere come è fatto un ammortizzatore, perché questo ci servirà per capire il seguito.
Eccovi dunque un disegno di un ammortizzatore come lo conoscete, cioè quello di una sospensione McPherson.

In realtà, esisterebbero moltissimi schemi (tipi) di ammortizzatori. Per esempio, le balestre svolgono la funzione di molle e quella di ammortizzatori, perché l’attrito tra le foglie delle balestre smorza le oscillazioni (infatti, le vetture a balestre sono particolarmente sconfortevoli, seppure robuste). Altro esempio, che sfrutta sempre lo stesso principio (attrito dovuto al movimento relativo, lo strisciamento, tra due corpi), quegli ammortizzatori composti da due “lame” infulcrate tra loro all’estremità e sporgenti rispetto all’asse ruote, che potete notare su molte auto anteguerra.
Noi, però, per semplicità, ci dedicheremo agli ammortizzatori idraulici telescopici.
Anche in questo caso, ci sono molte variazioni sul tema: classificazioni varie, etc. Diciamo che la classificazione principale riguarda il metodo secondo il quale si “dispone”, come varia, il volume di olio rispetto al pistone che scorre nel cilindro; e questo è un gran bel problema, perché l’olio è un fluido molto poco comprimibile e se devo garantire all’ammortizzatore una lunga corsa dello stelo, le cose si complicano un po’ (dove metto l’olio che sposto?).
Comunque, guardate la figura successiva:

Di base, ci sono tre tipi di ammortizzatore (telescopici idraulici):
a) telescopici con il fluido che passa tra le due camere
b) telescopici “bitubo”
c) telescopici a tubo singolo
Quelli di tipo a) risolvono il problema dello spostamento del fluido semplicemente spostandolo al di sopra e al di sotto del pistone. Questa soluzione ha indubbi vantaggi nell’ottimizzazione dello spazio (occupa poco spazio e posso collocarlo dove voglio) ma presenta lo svantaggio di sollecitare molto le guarnizioni di tenuta alle estremità del cilindro che contiene l’olio (che sono sottoposte ad elevate pressioni, col rischio di perdite di tenuta). Inoltre, quando lo stelo raggiunge la sua corsa massima, c’è l’elevato rischio di inconvenienti o danneggiamenti delle estremità e, infine, si deve tenere in qualche conto del fatto che l’olio, che si riscalda durante il funzionamento dell’ammortizzatore, varia anche di volume. Diciamo che, per le sospensioni, non va bene; al contrario, è molto usato come ammortizzatore di sterzo (è messo sugli sterzi).
Il tipo b) (bitubo) presenta due tubi coassiali: il cilindro esterno contiene del gas (comprimibile) che compensa la variazione di volume del cilindro durante lo scorrimento del pistone e il conseguente spostamento dell’olio. Questo è, generalmente, il tipo più usato nelle sospensioni.
Il gas c’è anche nel tipo c) (monotubo) e, generalmente, questo è emulsionato con l’olio; in alcuni casi, il gas è invece separato dall’olio da un ulteriore pistone (o una membrana robusta) che evita, appunto l’emulsione. Se guardate la figura c) vedrete questo setto di separazione. Questo particolare tipo di ammortizzatore monotubo è del tipo De Carbon (dal nome del suo inventore).
Vediamo ora da quali elementi è costituito un ammortizzatore e come funziona.
Consideriamo, per semplicità, un ammortizzatore idraulico monotubo. Ma i principi di funzionamento vanno bene anche per tutti gli altri tipi di ammortizzatori idraulici e idropneumatici (come ad es. i bitubo, gli idropneumatici, quelli ad alta e bassa pressione etc).
Osservate la figura successiva.
All’interno del cilindro, chiuso ad una estremità, scorre uno stantuffo (un pistone) solidale con uno stelo. Il cilindro da una parte e lo stelo, dall’altra, sono collegati l’uno alla sospensione e l’altro alla scocca.
Il tubo è riempito con l’olio; che in realtà proprio olio non è, ma è un fluido speciale che deve avere come caratteristica la capacità di mantenere la viscosità il più possibile stabile al variare della temperatura (che poi, anche qui, non si possono certo fare miracoli: provate a lasciare la macchina parcheggiata all’aperto una notte in montagna d’inverno. E poi, alla mattina, mettetevi in auto e partite: anche la più confortevole delle vetture, appena partite, vi sembrerà rigida come un carretto. Semplicemente perché gli ammortizzatori sono freddi; e freddo, denso e viscoso, sarà pure il fluido all’interno…).
Comunque, questo fluido trafila, durante il movimento del pistone, attraverso dei fori calibrati (delle valvole) ricavati sul pistone stesso. In funzione di come sono “calibrate” le valvole, ossia della loro sezione di passaggio attraverso cui scorre il fluido, si riesce a dare all’ammortizzatore la caratteristica (cioè la frenatura, ossia il coefficiente di smorzamento) che si vuole.

Del tutto simile al monotubo è il bitubo, costituito da 2 cilindri coassiali: uno di “lavoro”, dove scorre il pistone; l’altro di “riserva” dove finisce il fluido spostato dal pistone durante il movimento.

Poi, ci sarebbero anche gli ammortizzatori con il serbatoio del fluido separato ed esterno (tipo gli Ohlins da moto, tanto per citarne alcuni).
Le valvole di controllo, poste sul pistone e alla base della camera di “lavoro” (nel caso dell’ammortizzatore bitubo) sono un sistema composto da rondelle di spinta, molle a spirale e veri e propri corpi valvola accuratamente tarati.
Abbiamo chiarito come sono fatti gli ammortizzatori idraulici che, lo ripeto, sono ben diversi dagli ammortizzatori a frizione (come le balestre). È importante che capiate che sono differenti, perché adesso vedremo IN COSA lo sono (nel senso che uno potrebbe anche dire: e allora, perché non metto un ammortizzatore a frizione e la finiamo lì?).
Prima però, mi interessa che capiate bene un paio di concetti.
1) Attenti a non confondere le molle con gli ammortizzatori. Le prime lavorano “in dinamica e in statica”. Gli altri lavorano solo “in dinamica”. Deve essere chiaro. Insomma, se tolgo le molle e tengo solo gli ammortizzatori, la macchina si siede, si abbassa FINO AI TAMPONI. E se questi non ci sono, arrivo alla fine della compressione della sospensione e lì rimango. Punto. La macchina senza molle non funziona. Al limite, invece, potrei andare con solo le molle (salvo rimbalzare fuoristrada alla prima curva): la macchina mantiene il suo assetto statico e, ammettendo di rollare, beccheggiare, frenare, accelerare, girare il volante, etc in un tempo INFINITO (quindi, attraverso infiniti istanti di “transitorio esaurito”), riuscirei ad andare… Peccato che la realtà NON sia questa. Quindi, molle e ammortizzatori si completano a vicenda.
La forza esercitata dalla molla è funzione della posizione x (estensione e/o compressione) a meno di un coefficiente di proporzionalità.
La forza espressa dall’ammortizzatore è SOLO funzione della velocità (v, o x’) con cui si muove il pistone (lo stelo) rispetto al cilindro (tubo che contiene l’olio).
2) Nel sistema schematico molla – massa - ammortizzatore, non è ben chiaro COSA sia la massa, cioè QUANTO vale.
In precedenza, per fissare i concetti di base, avevamo detto che la massa M era la massa (la porzione di massa) sospesa. Invece, a differenza della molla e dell’ammortizzatore, che sono facilmente riconducibili agli elementi che costituiscono la sospensione, la massa M può essere intesa, alternativamente, come la massa sospesa o la massa NON sospesa.
Mi spiego meglio: supponiamo di stare percorrendo una strada ondulata. La scocca si muove rispetto alle ruote, che seguono il profilo stradale. In questo caso, è la scocca che si muove, quindi ricadiamo nel primo caso: massa SOSPESA che si muove. E quindi la mia M è la massa sospesa (o quella porzione di massa sospesa che compete alla sospensione che sto considerando).
Invece, se affronto un gradino, o una buca , e la ruota si stacca dal terreno, quindi si muove rispetto alla scocca, che massa considero? La massa NON sospesa, perché è la ruota.
Bene: mi sembra chiaro che le masse sono MOLTO differenti. Ruota e scocca hanno masse MOLTO differenti, inerzie MOLTO differenti; ma anche velocità MOLTO differenti….per cui l’ammortizzatore dovrà fornire differenti forze di smorzamento. Ossia, differente dovrà essere la forza di smorzamento che l’ammortizzatore fornisce durante i due movimenti (che possono accadere; anzi, è normalissimo che accadano quando si viaggia).
Allora, come possiamo fare? Semplice, adottando due differenti tipi di valvole.
Il fatto è che ad un ammortizzatore si richiede che abbia almeno due caratteristiche differenti di smorzamento: una, modesta, per smorzare i moti della cassa (la massa sospesa), che sono lenti; un’altra, più energica, più forte, per smorzare i moti delle ruote (masse NON sospese), che sono più veloci.
Prima di vedere come sia la caratteristica di un ammortizzatore, vediamo come si realizza questa condizione. Sulla base della considerazione 2): con le valvole. Cioè, le differenti caratteristiche, quella modesta per smorzare i moti lenti delle masse sospese e quella forte per i moti delle masse non sospese, si ottengono con i fori calibrati.
Una serie di fori piccoli e SEMPRE APERTI frenano i moti lenti, perché consentono il passaggio continuo del fluido tra le due camere che il pistone crea all’interno del cilindro di lavoro.
Un’altra serie di fori grandi, ma dotati di valvole di chiusura opportunamente tarate, frenano i moti rapidi delle ruote. Le valvole si aprono automaticamente al raggiungimento di una soglia di pressione e di una quantità tanto più grande quanto maggiore è la pressione che il fluido esercita su di esse durante i moti veloci delle ruote. Sono, insomma, delle valvole PROPORZIONALI (normalmente chiuse). Ora, visto che la pressione che il liquido esercita sulle valvole è funzione diretta della velocità del pistone (e quindi dello stelo dell’ammortizzatore), quanto più veloce andrà lo stelo, cioè in definitiva la ruota, tanto maggiore sarà la forza che “frena” la ruota nel suo movimento (verticale).
È chiaro che, se non ci fossero queste valvole calibrate, in corrispondenza dei fori di grosso diametro, a regolare la forza che contrasta il moto delle masse non sospese e ci affidassimo solo ai fori calibrati di piccolo diametro (che gestiscono i moti lenti delle masse sospese), le resistenze idrauliche (le perdite di carico) generate dal fluido nel passaggio per questi fori sarebbero talmente elevate da rendere, di fatto, l’ammortizzatore troppo “duro” (passatemi il termine scorretto, ma è per farvi capire); troppo frenato, troppo “rigido”.
Al contrario, l’assenza delle valvole calibrate nei fori grandi lascerebbe troppo “libero” l’ammortizzatore nei moti lenti della scocca (masse sospese), rendendo l’ammortizzatore troppo “morbido”. E la mia BMW diventerebbe una Citroen…
Infatti, le valvole restano chiuse nei moti lenti (basse velocità dello stelo, e quindi del fluido) e obbligano il fluido a passare per i fori piccoli. Oltre un certo valore di ΔP, cioè di differenza di pressione tra le due facce del pistone (tra le due camere di lavoro del cilindro), le valvole si aprono IN PROPORZIONE ALLA PRESSIONE (e quindi alla velocità dello stelo)…
Va considerato perciò che l’ammortizzatore NON lavora solo in un senso, per esempio solo in compressione, ma anche in estensione. Ossia, lavora sia quando la sospensione si comprime (a tamponamento), sia quando si estende (a rimbalzo). Ora, il fatto che l’ammortizzatore lavori nei due sensi, lo qualifica come ammortizzatore A DOPPIO EFFETTO.
Questa caratteristica lo distingue dagli ammortizzatori più semplici detti A SEMPICE EFFETTO perché agiscono (lavorano) solo in un senso.
Allora, possiamo andare a vedere le curve caratteristiche che appunto descrivono il funzionamento dell’ammortizzatore.
:grazie) alfistavero

